Đáp án C

\(2x-y=m\Leftrightarrow y=2x-m\\ x-y=2m\Leftrightarrow y=x-2m\)

PT hoành độ giao điểm 2 đt đầu: \(2x-m=x-2m\Leftrightarrow x=-m\Leftrightarrow y=-3m\Leftrightarrow A\left(-m;-3m\right)\)

Để 3 đt đồng quy thì \(A\left(-m;-3m\right)\in mx-\left(m-1\right)y=2m-1\)

\(\Leftrightarrow-m^2+3m\left(m-1\right)=2m-1\\ \Leftrightarrow2m^2-5m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{5+\sqrt{17}}{4}\\m=\dfrac{5-\sqrt{17}}{4}\end{matrix}\right.\)

Đáp án C

Đáp án D

Gọi A là giao điểm của \(y=2x-1\) và \(y=x+2\)

Hoành độ A thỏa mãn:

\(2x-1=x+2\Rightarrow x=3\)

\(\Rightarrow y=5\)

\(\Rightarrow A\left(3;5\right)\)

3 đường thẳng đồng quy khi  \(y=\left(2m+3\right)x-m+1\) đi qua A

\(\Rightarrow5=3\left(2m+3\right)-m+1\)

\(\Rightarrow m=-1\)

a/ Trong quá trình tìm m để các đường thẳng đồng quy đã có phân biệt rồi. Vì nếu k phân biệt thì trùng nhau, mà trùng nhau thì chỉ là 1 đường thẳng ko thể đồng quy được.

Vì 3 đt đồng quy

Xét PTHĐGĐ của đt y= mx+3 và đt y= 3x+m

mx+3= 3x+m

<=> x(m+3)= (m+3)

<=> x=1; y= m+3

Thay vào y= -5x-5

-5-5= m+3

<=> m= -13

câu b tg tự

b)

Ta có phương trình hoành độ giao điểm của hai đường thẳng \(y=2x\) và \(y=-3-x\):

\(\left\{{}\begin{matrix}y=2x\\y=-3-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)

Thay x=-1 và y=-2 vào phương trình đường thẳng \(y=mx+5\) ta có:

\(y=mx+5\Leftrightarrow-2=-m+5\Leftrightarrow m=7\)

Đáp án B

+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:

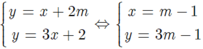
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)

+  Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có

3m-1= -m( m-1) + 2 hay m²+ 2m-3=0

Suy ra m=1 hoặc m= -3

Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ :  y= 3x+ 2 và d’’: y= -x+ 2  phân biệt và đồng quy tại M(0; 2).

Với m= -3  ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn

Vậy m= 1 là giá trị cần tìm.

Chọn B.

a. Gọi A là điểm 3 đường thẳng đồng quy

Phương trình hoành độ giao điểm của d1 và d2: 4/3x + 1= x-1 ⇔ 1/3x = -2 ⇔ x = -6

thay x = -6 vào d2 ⇒ y = -6 -1 = -7 

Vậy A(-6;-7)

Để 3 đường thẳng đồng quy thì A thuộc d3 ⇒ -7 = m.(-6) + m+ 3

                                                                       ⇔ -7 = -6m + m + 3

                                                                        ⇔ -5m = -10

                                                                      ⇔ m=2

câu b 

a. Gọi A là điểm 3 đường thẳng đồng quy

Phương trình hoành độ giao điểm của d1 và d2: x - m + 1= 2x ⇔ x = -m +1

thay x = -m +1 vào d2 ⇒ y = 2.(-m +1) = -2m +2

Vậy A(-m +1;-2m +2)

Để 3 đường thẳng đồng quy thì A thuộc d3 ⇒ -2m +2 = 2(2m-1).(-m +1) + 1/4

                                                                       ⇔ -2m +2 = -4m² +4m +2m-2 + 1/4

                                                                        ⇔   4m² - 8m +15m/4=0

Giai pt bậc 2 được m=5/4 và m=3/4