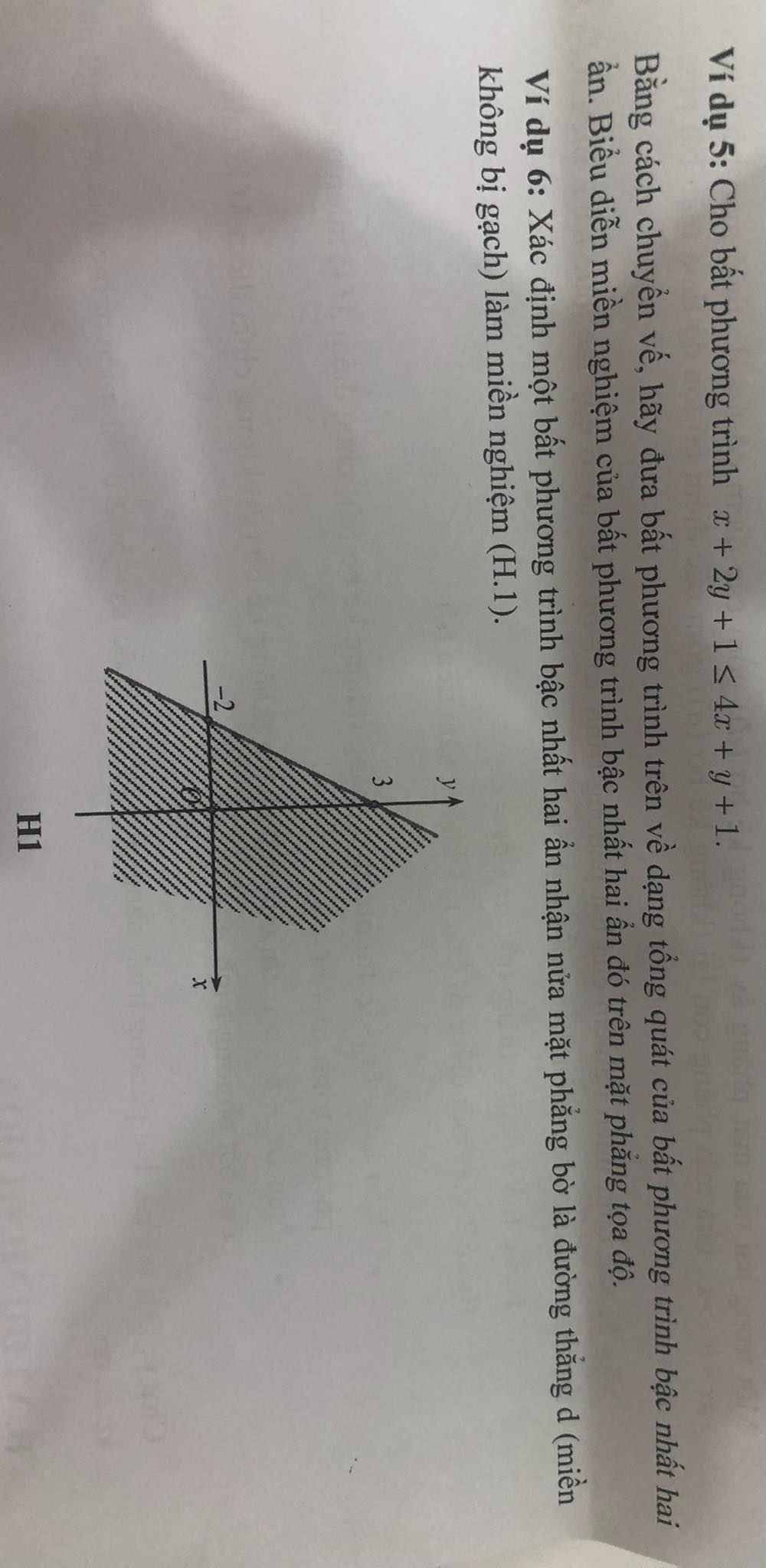
Xác định (P) y = ax² + bx + c, biết (P) đi qua M(8;0) và đỉnh I(-6;12)
§2. Hàm số y=ax+b
Thay x=8 và y=0 vào (P), ta được:
\(a\cdot8^2+b\cdot8+c=0\)
=>64a+8b+c=0(1)
Đỉnh I(-6;12) nên ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-6\\-\dfrac{b^2-4ac}{4a}=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=12a\\b^2-4ac=-48a\end{matrix}\right.\)(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}b=12a\\b^2-4ac=-48a\\64a+8b+c=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=12a\\144a^2+48a-4ac=0\\64a+96a+c=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=12a\\36a+12-c=0\\160a+c=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=12a\\36a-c=-12\\160a+c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=12a\\196a=-12\\c=-160a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-\dfrac{3}{49}\\b=-\dfrac{36}{49}\\c=-160\cdot\dfrac{-3}{49}=\dfrac{480}{49}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
x2+y3?
Câu T. Cho parabol (P): y= x +5x-6. Xác định trục đối xứng, tọa độ đinh của parabol (P), tọa độ giao điểm của parabol (P) với trục hoành.
Sửa đề: (P): \(y=x^2+5x-6\)
Tọa độ đỉnh của (P) là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=-\dfrac{5}{2}\\y=-\dfrac{\text{Δ}}{4a}=-\dfrac{5^2-4\cdot1\cdot\left(-6\right)}{4\cdot1}=-\dfrac{25+24}{4}=-\dfrac{49}{4}\end{matrix}\right.\)
=>Trục đối xứng của (P) là \(x=-\dfrac{5}{2}\)
Tọa độ giao điểm của (P) với trục Ox sẽ là nghiệm của hệ phương trình sau đây:
\(\left\{{}\begin{matrix}x^2+5x-6=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+6\right)\left(x-1\right)=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{-6;1\right\}\\y=0\end{matrix}\right.\)
Vậy: Tọa độ các giao điểm của (P) với trục Ox là A(-6;0) và B(1;0)
Đúng 1
Bình luận (0)
VD5:
x+2y+1<=4x+y+1
=>\(x+2y+1-4x-y-1< =0\)
=>\(-3x+y< =0\)
Vậy: Dạng tổng quát của bất phương trình này là -3x+y<=0
-3x+y<=0
=>y<=3x
Thay x=0 và y=0 vào BPT -3x+y<=0, ta được:
\(-3\cdot0+0< =0\)
=>0<=0(luôn đúng)
Vậy: Miền nghiệm của BPT -3x+y<=0 sẽ là nửa mặt phẳng chứa biên là đường thẳng y=3x và chứa luôn điểm O(0;0)
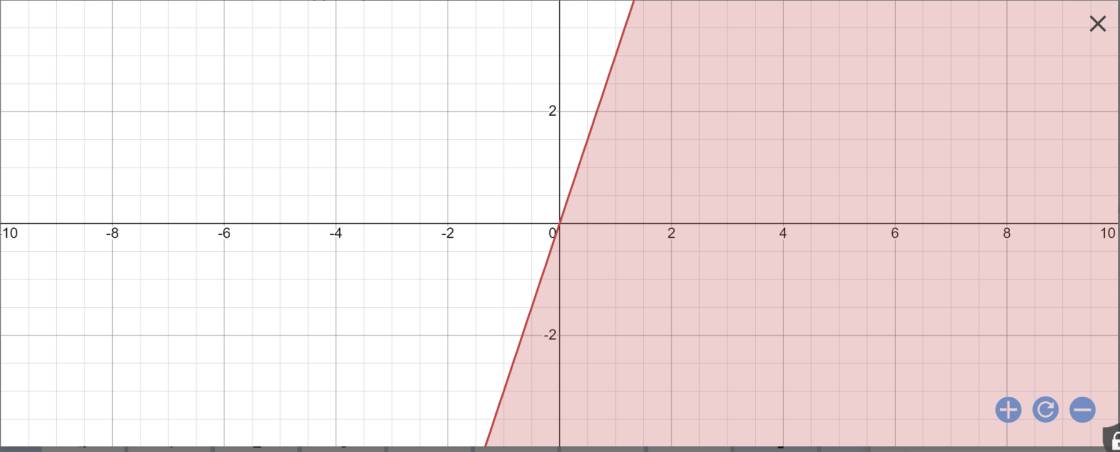
Đúng 0
Bình luận (0)
Vd8:
a: x-3y>=0
=>3y<=x
=>y<=x/3
Đặt (d): y=x/3
Thay x=0 và y=0 vào BPT y<=x/3, ta được:
\(0< =\dfrac{0}{3}=0\)(đúng)
Vậy: Miền nghiệm của BPT x-3y>=0 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
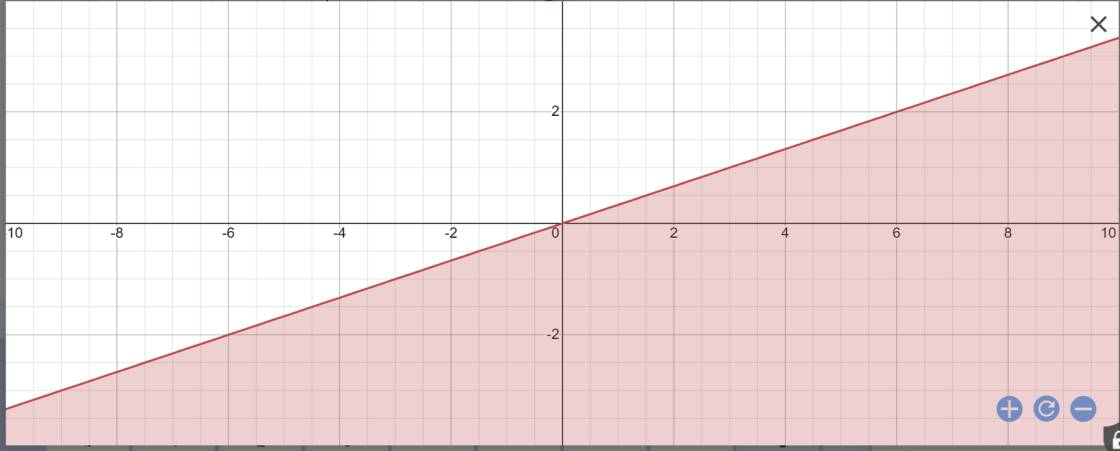
b: \(\dfrac{x-y}{-2}< x+y+1\)
=>\(-\dfrac{1}{2}x+\dfrac{1}{2}y< x+y+1\)
=>\(-\dfrac{1}{2}x+\dfrac{1}{2}y-x-y< 1\)
=>\(-\dfrac{3}{2}x-\dfrac{1}{2}y< 1\)
=>\(-3x-y< 2\)
Gọi (d1): -3x-y=2
=>y=-3x-2
Thay x=0 và y=0 vào BPT -3x-y<2, ta được:
\(-3\cdot0-0< 2\)
=>0<2(đúng)
Vậy: Miền nghiệm của bất phương trình \(\dfrac{x-y}{-2}< x+y+1\) là nửa mặt phẳng không chứa biên nhưng chưa điểm O(0;0)
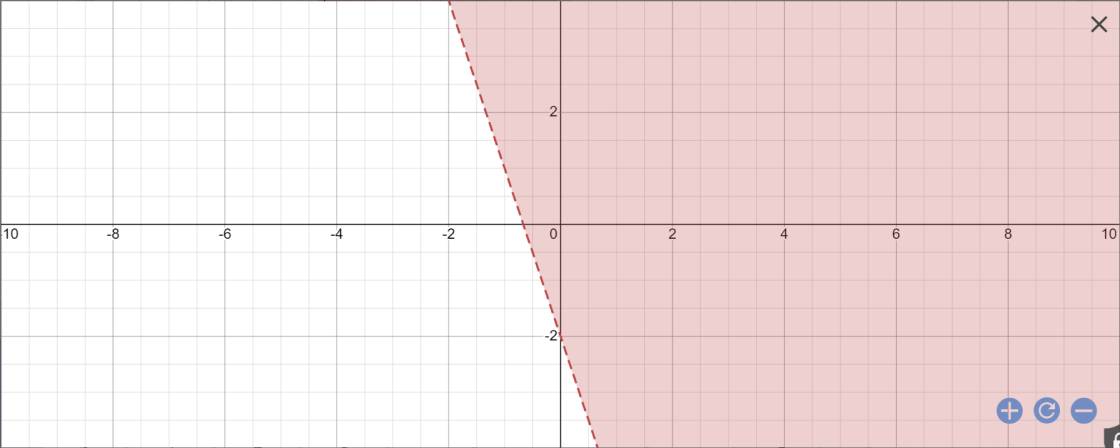
Đúng 0
Bình luận (0)
Giải hộ mình câu 28 với ạ 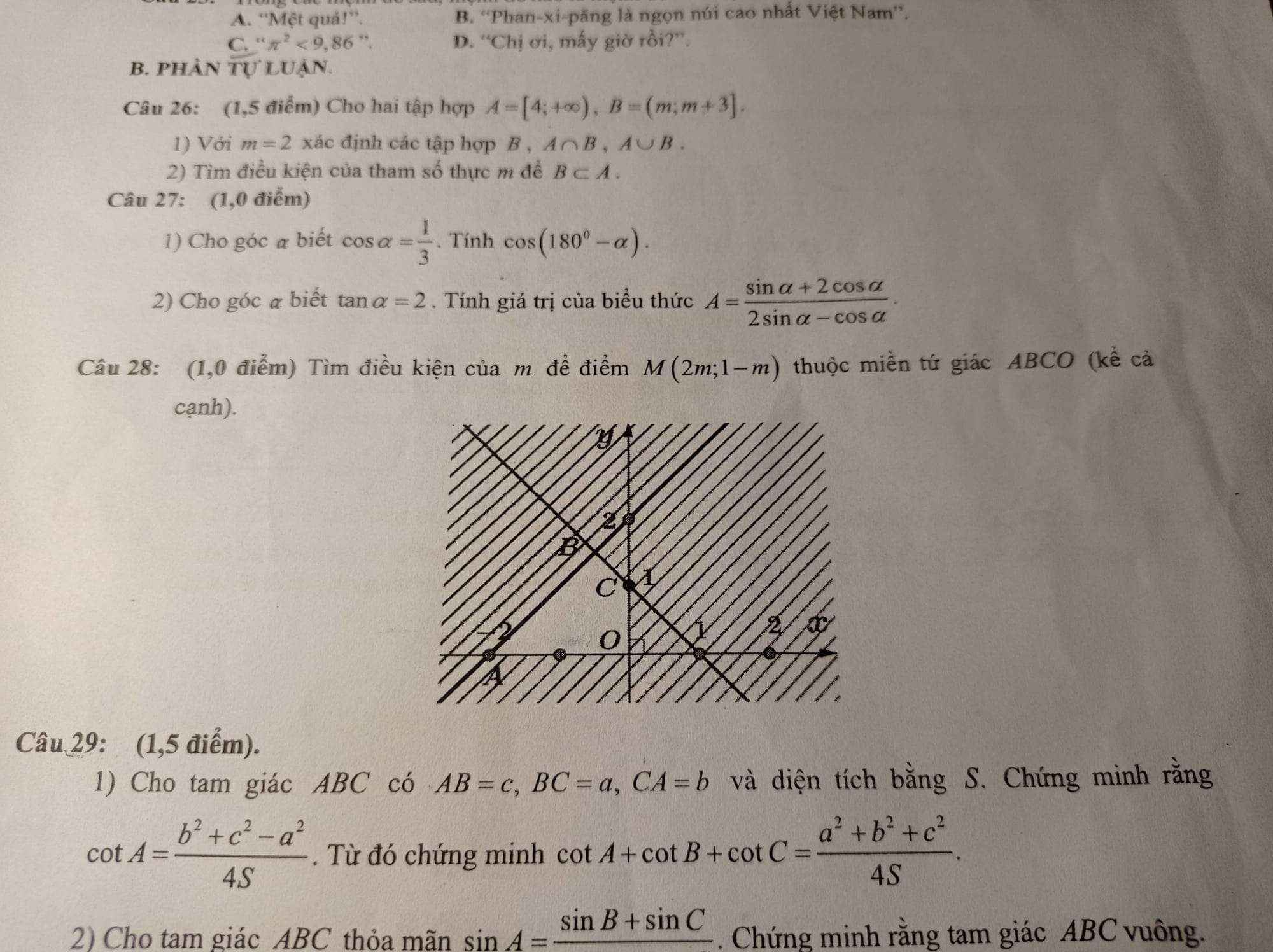
Giúp mình với
Câu 1 : Có tất cả bao nhiêu giá trị nguyên của than số m lớn hơn -10 để hàm số y= \(\dfrac{3x^2+2x+1}{x^2-6x+4-m}\) xác định với mọi giá trị x∈(6;+∞)?
TH1: \(x^2-6x+4-m=0\) vô nghiệm
\(\Rightarrow\Delta'=9-\left(4-m\right)< 0\Rightarrow m< -5\)
TH2: \(x^2-6x+4-m=0\) có nghiệm thỏa mãn \(x_1\le x_2\le6\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m+5\ge0\\f\left(6\right)=36-6.6+4-m\ge0\\\dfrac{x_1+x_2}{2}=3< 6\end{matrix}\right.\) \(\Rightarrow-5\le m\le4\)
Kết hợp lại ta được \(m\le4\)
Đúng 1
Bình luận (2)
E cảm ơn ạ 
\(y=\sqrt{3x-m+1}.\)
ĐKXĐ: \(3x-m+1\ge0.\\ \Leftrightarrow3x\ge-1+m.\\ \Leftrightarrow x\ge\dfrac{m-1}{3}.\)
\(D=[\dfrac{m-1}{3};+\infty).\)
Để hàm số xác định trên khoảng \(\left(1;+\infty\right).\)
\(\left(1;+\infty\right)\subset[\dfrac{m-1}{3};+\infty).\\ \Rightarrow\dfrac{m-1}{3}\le1.\\ \Leftrightarrow\dfrac{m-1}{3}-1\le0.\\ \Leftrightarrow\dfrac{m-1-3}{3}\le0.\\ \Leftrightarrow\dfrac{m-4}{3}\le0.\\ \Rightarrow m-4\le0.\\ \Leftrightarrow m\le4.\)
Đúng 0
Bình luận (0)
Xác định các hệ số của a và b để đồ thị của hàm số y = ax + b đi qua điểm M(1; 7) và N(0; 3).
Hàm số y = ax + b đi qua điểm M(1; 7).
\(\Rightarrow7=a+b.\left(1\right)\)
Hàm số y = ax + b đi qua điểm N(0; 3).
\(\Rightarrow3=b.\left(2\right)\)
Thay (2) vào (1), ta có:
\(7=a+3.\Leftrightarrow a=4.\)
Vậy các hệ số a và b là 4 và 3.
Đúng 2
Bình luận (0)