Cho tấm giác ABC vuông tại A.đg cao AH. Cho biết AB=6cm,AC=8cm. Tính tất cả các cạnh còn lại.
HM
Những câu hỏi liên quan
ai biết giải giúp minh với:Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minha,tứ giác HECD nội tiếpb,Tia DA là tia phân giác góc EDK Cây 2:cho tam giác ABC vuông tai A,biết ab6cm,ac8cmA.tính bcB,kẻ đường cao AH,tính Ah Câu 3:Cho tam giác abc vuông tại A,BIẾT AC4cm,Bc5cm.A,Tính cạnh ABB,kẻ đường cao AH,TÍNH AHCâu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB12CM,AC5CM.tính BH,CHCâu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC18cm,B...
Đọc tiếp
ai biết giải giúp minh với:
Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minh
a,tứ giác HECD nội tiếp
b,Tia DA là tia phân giác góc EDK
Cây 2:cho tam giác ABC vuông tai A,biết ab=6cm,ac=8cm
A.tính bc
B,kẻ đường cao AH,tính Ah
Câu 3:Cho tam giác abc vuông tại A,BIẾT AC=4cm,Bc=5cm.
A,Tính cạnh AB
B,kẻ đường cao AH,TÍNH AH
Câu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB=12CM,AC=5CM.tính BH,CH
Câu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC=18cm,BH=6cm.Tính độ dài các cạnh AB,AC
Cau 6:Cho tam giác ABC,vuông tại A,biết AB=4cm,đường cao AH=2CM,tính các góc và các cạnh còn lại cua tam giac.?
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
Đúng 1
Bình luận (0)
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH . Trong các đoạn thẳng sau đây : AB,AC,BC,AH,HB,HC hãy tính các đoạn thẳng còn lại nếu biết :
a. AB=6cm , AC=8cm
b. AH=9,6cm ,HC=12,8cm
c. AH=12cm , BC=25cm
d. AB=15cm , HB=9cm
e. HB=12,5cm , HC=7,2cm
a.
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm) theo định lý Pitago
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6$ (cm) theo định lý Pitago
$CH=BC-BH=10-3,6=6,4$ (cm)
b.
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Rightarrow BH=\frac{AH^2}{CH}=\frac{AH^2}{CH}=\frac{9,6^2}{12,8}=7,2$ (cm)
$BC=BH+CH=7,2+12,8=20$ (cm)
$AB=\sqrt{AH^2+BH^2}=\sqrt{9,6^2+7,2^2}=12$ (cm) theo Pitago
$AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-12^2}=16$ (cm) theo Pitago
Đúng 1
Bình luận (0)
c.
$AB.AC=AH.BC=12.25=300$
$AB^2+AC^2=BC^2=625$
$(AB+AC)^2-2AB.AC=625$
$AB+AC=\sqrt{625+2AB.AC}=\sqrt{625+2.300}=35$
Áp dụng Viet đảo thì $AB,AC$ là nghiệm của:
$X^2-35X+300=0$
$\Rightarrow (AB,AC)=(20,15)$ (giả sử $AB>AC$)
$BH=\sqrt{AB^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
Đúng 1
Bình luận (0)
d.
Áp dụng HTL trong tam giác vuông:
$AB^2=BH.BC$
$\Rightarrow BC=\frac{AB^2}{HB}=\frac{15^2}{9}=25$ (cm)
$CH=BC-BH=25-9=16$ (cm)
Áp dụng HTL:
$AH=\sqrt{BH.CH}=\sqrt{9.16}=12$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
e.
$BC=BH+CH=12,5+7,2=19,7$ (cm)
$AH=\sqrt{HB.HC}=\sqrt{12,5.7,2}=3\sqrt{10}$ (cm)
$AB=sqrt{AH^2+BH^2}=\sqrt{(3\sqrt{10})^2+12,5^2}=\frac{\sqrt{985}}{2}$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{(3\sqrt{10})^2+7,2^2}=\frac{3\sqrt{394}}{5}$ (cm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Kẻ đường cao AH. Tính độ dài cạnh AH.
Theo \(pi-ta-go\) ta có : \(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\) \((cm)\)
Áp dụng hệ thức lượng vào tam giác \(ABC\) vuông và đường cao \(AH\) ta có :
\(AH.BC=AB.AC\)\(\Rightarrow\) \(AH=\dfrac{6.8}{10}=4,8(cm)\)
Đúng 1
Bình luận (0)
- Áp dụng định lý Pytago
=> BC=10 (cm)
- Gọi HB=a (cm) ; HC=b (cm)
=> a+b=BC=10 (1)
- Xét \(\Delta\)HBA và \(\Delta\)ABC có:
BHA=BAC=90\(^o\)
BAC chung
=> \(\Delta\)HBA ~ \(\Delta\)ABC (g.g)
=> \(\dfrac{BH}{AB}\)=\(\dfrac{AB}{BC}\) (cạnh t/ư)
=> BH.BC=AB2 (tỉ lệ thức)
thay số: a.10= 36 (2)
Từ (1)(2) => a=3,6 (cm); b=6,4 (cm)
- Áp dụng Pytago cho \(\Delta\)HBA
=> AH2=AB2- HB2 =36-12,96=23,04 (cm)
=> AH=4,8 (cm)
P/s: Vì không nhớ lớp 8 học hệ thức lượng chưa nên đành phải lôi thôi thế này :<<<<
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác vuông ABC vuông tại A có AB=6cm,AC=8cm. Kẻ đường cao AH. a) Chứng minh tam giác ABC đồng dạng với tam giác HBA b) Tính độ dài các cạnh BC, AH ,BH
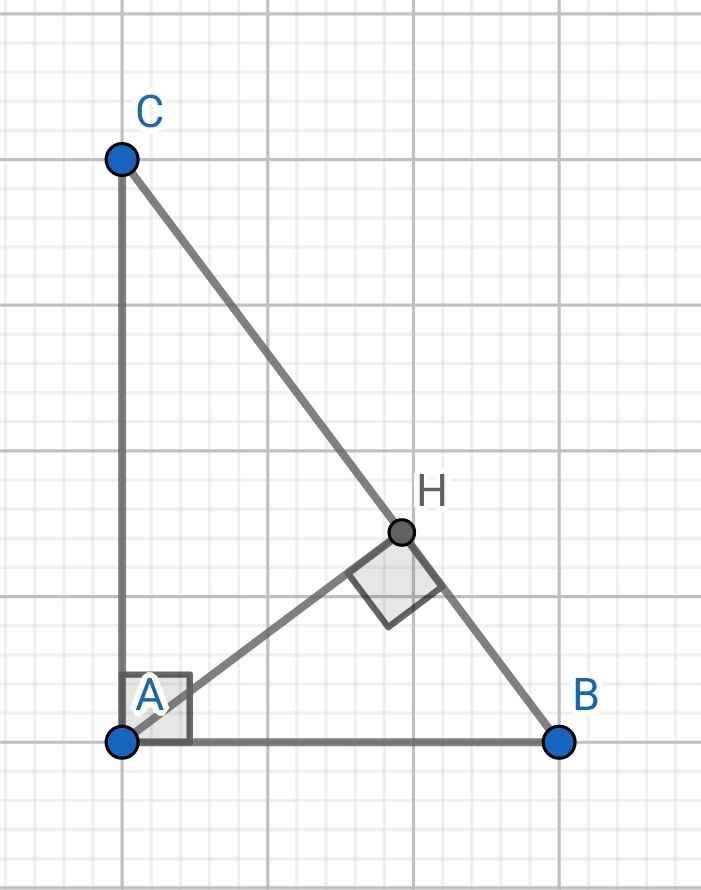
a) Xét hai tam giác vuông: ∆ABC và ∆HBA có:
∠B chung
⇒ ∆ABC ∽ ∆HBA (g-g)
b) ∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10
Do ∆ABC ∽ ∆HBA (cmt)
⇒ AC/AH = BC/AB
⇒ AH = AB.AC/BC
= 6.8/10
= 4,8 (cm)
∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
⇒ BH² = AB² - AH²
= 6² - (4,8)²
= 12,96
⇒ BH = 3,6 (cm)
Đúng 3
Bình luận (0)
a) Ta có:
- Góc A của tam giác ABC là góc vuông, nên ta có thể tính được độ dài đoạn thẳng AH bằng cách sử dụng định lí Pythagoras: AH = sqrt(AB^2 + AC^2) = sqrt(6^2 + 8^2) = 10.
- Góc A của tam giác ABC cũng là góc giữa đường cao AH và cạnh huyền BC, nên ta có thể tính được tỉ số giữa độ dài đoạn thẳng AH và độ dài cạnh huyền BC: AH/BC = AC/AB = 8/6 = 4/3.
- Từ tỉ số này, ta có thể suy ra rằng tam giác ABC đồng dạng với tam giác HBA (vì cả hai tam giác có cùng một góc và tỉ số giữa các cạnh tương ứng bằng nhau).
b) Để tính độ dài các cạnh BC, AH, BH, ta có thể sử dụng các công thức sau:
- Độ dài cạnh BC: BC = AB/AC * AH = 6/8 * 10 = 15/2 = 7.5.
- Độ dài đoạn thẳng BH: BH = sqrt(AH^2 - AB^2) = sqrt(10^2 - 6^2) = 8.
- Độ dài đoạn thẳng AH đã được tính ở trên: AH = 10.
Vậy độ dài các cạnh BC, AH, BH lần lượt là 7.5cm, 10cm, 8cm.
Đúng 1
Bình luận (0)
Cho D ABC vuông tại A có AB = 6cm, AC = 8cm, BC = 10cm, đường cao AH a) Viết các hệ thức giữa cạnh và đường cao AH trong tam giác ABC. b) Tính AH, BH, CH
a) Các hệ thức giữa cạnh và đường cao AH:
\(AH^2=BH.CH\)
\(AB^2=BH.BC\)
\(AC^2=CH.BC\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(AH.BC=AB.AC\)
b) Áp dụng HTL trong tam giác ABC vuông tại A có đg cao AH:
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
Ta có: \(AB^2=BH.BC\)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
\(BC=CH+BH\)
\(\Rightarrow CH=BC-BH=10-3,6=6,4\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=6cm, AC=8cm, BC=10cm. Tính AH
Cho tam giác ABC vuông ở A , AB=6cm; AC=8cm; BC=10cm có đường cao AH cắt cạnh BC tại H, đường phân giác BD của góc ABC cắt AC tại D.
a) Tính độ dài các đoạn thẳng AD và DC .
b) Tính AH=?
a/ \(BD\) là đường phân giác \(\widehat{BAC}\)
\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\to\begin{cases}DA=3\\DC=5\end{cases}\)
b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)
\(\to AB.AC=AH.BC\)
\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)
Đúng 1
Bình luận (0)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A, biết AH 16, BH 9. Tính AB.2. Cho tam giác ABC vuông tại A, AB 6cm, AC 8cm. Tính độ dài HB.3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12, BC 15. Tính HC.4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 6, HC 9. Tính độ dài AC.5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12cm, BC 16cm. Tính AH6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 8cm, HC 12 cm. Tính AC.
Đọc tiếp
1. Cho tam giác ABC vuông tại A, biết AH = 16, BH = 9. Tính AB.
2. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài HB.
3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12, BC = 15. Tính HC.
4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 6, HC = 9. Tính độ dài AC.
5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 16cm. Tính AH
6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 8cm, HC = 12 cm. Tính AC.
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
Đúng 1
Bình luận (3)
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AB 9cm, BC 15cm. Tính BH, HC b) Biết BH 1cm, HC 3cm. Tính AB, AC c) Biết AB 6cm, AC 8cm. Tính AH, BCBài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, BH 2,4cm a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc BBài 3: Cho tam giác ABC có BC 9cm, góc B 60 độ, góc C 40 độ, đường cao AH. Tính AH, AB, AC
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB= 9cm, BC= 15cm. Tính BH, HC
b) Biết BH= 1cm, HC= 3cm. Tính AB, AC
c) Biết AB= 6cm, AC= 8cm. Tính AH, BC
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB= 3cm, BH= 2,4cm
a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc B
Bài 3: Cho tam giác ABC có BC= 9cm, góc B= 60 độ, góc C= 40 độ, đường cao AH. Tính AH, AB, AC
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)









