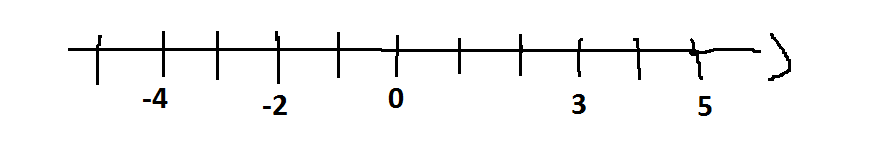Nè bạn

\(x+\sqrt{4-x^2}=2\)

\(\Leftrightarrow4-x^2=\left(2-x\right)^2\)

\(\Leftrightarrow4-x^2=4-8x+x^2\)

\(\Leftrightarrow4-x^2-4+8x-x^2=0\)

\(\Leftrightarrow8x-2x^2=0\)

\(\Leftrightarrow2x\left(4-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\4-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

\(x+\sqrt{1-x^2}=1\)

\(\Leftrightarrow1-x^2=\left(1-x\right)^2\)

\(\Leftrightarrow1-x^2=1-2x+x^2\)

\(\Leftrightarrow1-x^2-1+2x-x^2=0\)

\(\Leftrightarrow2x-2x^2=0\)

\(\Leftrightarrow2x\left(1-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\1-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

\(a,\dfrac{1}{2}x=3+2\)

\(\dfrac{1}{2}x=5\)

\(x=5\div\dfrac{1}{2}\)

\(x=10\)

\(b,\dfrac{1}{4}x^2-\sqrt{36}=10\)

\(\dfrac{1}{4}x^2-6=10\)

\(\dfrac{1}{4}x^2=10+6\)

\(\dfrac{1}{4}x^2=16\)

\(x^2=16\div\dfrac{1}{4}\)

\(x^2=64\)

\(x^2=\left(8\right)^2\)

\(\Rightarrow x=8\)

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:

\(AM\cdot AB=AH^2\)(1)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:

\(AN\cdot AC=AH^2\)(2)

Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

She likes playing guitar.

dài thế

Đặt \(A=\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\)

\(\Leftrightarrow A^3=2+\sqrt{5}+2-\sqrt{5}+3\cdot\sqrt[3]{\left(2+\sqrt{5}\right)\left(2-\sqrt{5}\right)}\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)\)

\(\Leftrightarrow A^3=4+3\cdot\left(-1\right)\cdot A\)

\(\Leftrightarrow A^3=4-3A\)

\(\Leftrightarrow A^3+3A-4=0\)

\(\Leftrightarrow A^3-A^2+A^2-A+4A-4=0\)

\(\Leftrightarrow A^2\left(A-1\right)+A\left(A-1\right)+4\left(A-1\right)=0\)

\(\Leftrightarrow\left(A-1\right)\left(A^2+A+4\right)=0\)

\(\Leftrightarrow A=1\)

3) Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m^2-6\right)\)

\(=\left(2m-2\right)^2-4\left(m^2-6\right)\)

\(=4m^2-8m+4-4m^2+24\)

\(=-8m+28\)

Để phương trình có hai nghiệm phân biệt x1;x2 thì Δ>0

\(\Leftrightarrow-8m+28>0\)

\(\Leftrightarrow-8m>-28\)

hay \(m< \dfrac{7}{2}\)

Áp dụng hệ thức Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{1}=2m-2\\x_1x_2=m^2-6\end{matrix}\right.\)

Ta có: \(x_1^2+x_2^2=16\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)

\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-6\right)-16=0\)

\(\Leftrightarrow4m^2-8m+4-2m^2+12-16=0\)

\(\Leftrightarrow2m^2-8m=0\)

\(\Leftrightarrow2m\left(m-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=4\left(loại\right)\end{matrix}\right.\)