\(\lim\limits_{x\rightarrow+\infty}\left(x+1\right)\left(\sqrt{\dfrac{x}{2x^4+x^2+1}}\right)\)
H24
Những câu hỏi liên quan
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt[3]{3x^3+1}-\sqrt{2x^2+x+1}}{\sqrt[4]{4x^4+2}}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2x+1\right)^3\left(x+2\right)^4}{\left(3-2x\right)^7}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{4x^2-3x+4}-2x}{\sqrt{x^2+x+1}-x}\)
Da nan roi mang meo lam mat het bai -.-
1/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt[3]{\dfrac{3x^3}{x^3}+\dfrac{1}{x^3}}+\sqrt{\dfrac{2x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}}{-\sqrt[4]{\dfrac{4x^4}{x^4}+\dfrac{2}{x^4}}}=\dfrac{-\sqrt[3]{3}-\sqrt{2}}{\sqrt[4]{4}}\)
2/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{8x^7}{\left(-2x^7\right)}=-\dfrac{8}{2^7}\)
3/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(4x^2-3x+4-4x^2\right)\left(\sqrt{x^2+x+1}+x\right)}{\left(x^2+x+1-x^2\right)\left(\sqrt{4x^2-3x+4}+2x\right)}=\dfrac{-3.2}{2}=-3\)
Đúng 1
Bình luận (0)
1, Tính:
a, \(\lim\limits_{x\rightarrow-2}\dfrac{x^3+2x^2}{\sqrt{x^2+4x+4}}\)
b, \(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x+\sqrt{x+1}}-\sqrt{x}\right)\)
c, \(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2-x}+1+\sqrt[3]{x^3+2}\right)\)
\(\lim\limits_{x\rightarrow-2}\dfrac{x^3+2x^2}{\sqrt{x^2+4x+4}}=\lim\limits_{x\rightarrow-2}\dfrac{x^2\left(x+2\right)}{\sqrt{\left(x+2\right)^2}}\)
\(=\lim\limits_{x\rightarrow-2}x^2=\left(-2\right)^2=4\)
p/s: bài này mình chưa học trên lớp nên ko chắc 100% đúng
Đúng 0
Bình luận (0)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x+1}}{\sqrt{x+\sqrt{x+1}}+\sqrt{x}}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{1+\dfrac{1}{x}}}{\sqrt{1+\sqrt{\dfrac{1}{x}+\dfrac{1}{x^2}}}+1}=\dfrac{1}{1+1}=\dfrac{1}{2}\)
Câu c số 1 trong hay ngoài căn nhỉ?
Đúng 0
Bình luận (0)
limlimits_{xrightarrow-infty}left(x-sqrt{x^2+x+1}right)limlimits_{xrightarrowpminfty}left(sqrt{x^2+3x+1}-sqrt{x^2-x+1}right)limlimits_{xrightarrow+infty}left(sqrt[3]{8x^3+2x}-2xright)limlimits_{xrightarrow+infty}left(sqrt[4]{16x^4+3x+1}-sqrt{4x^2+2}right)limlimits_{xrightarrow+infty}left(sqrt{x^2+1}+sqrt{x^2-x}-2xright)
Đọc tiếp
\(\lim\limits_{x\rightarrow-\infty}\left(x-\sqrt{x^2+x+1}\right)\)
\(\lim\limits_{x\rightarrow\pm\infty}\left(\sqrt{x^2+3x+1}-\sqrt{x^2-x+1}\right)\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt[3]{8x^3+2x}-2x\right)\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt[4]{16x^4+3x+1}-\sqrt{4x^2+2}\right)\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+1}+\sqrt{x^2-x}-2x\right)\)
1/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2-x^2-x-x}{x+\sqrt{x^2+x+1}}=\dfrac{-2}{1-1}=-\infty\)
2/ tien toi +- vo cung?
3/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{8x^3+2x-8x^3}{\sqrt[3]{\left(8x^3+2x\right)^2}+2x.\sqrt[3]{8x^3+2x}+4x^2}=\dfrac{\dfrac{2x}{x^2}}{\dfrac{4x^2}{x^2}+\dfrac{4x^2}{x^2}+\dfrac{4x^2}{x^2}}=0\)
4/ \(\lim\limits_{x\rightarrow+\infty}\dfrac{16x^4+3x+1-16x^4}{\sqrt[4]{\left(16x^4+3x+1\right)^3}+2x.\sqrt[4]{\left(16x^4+3x+1\right)^2}+4x^2.\sqrt[4]{16x^4+3x+1}+8x^3}+\lim\limits_{x\rightarrow+\infty}\dfrac{4x^2-4x^2-2}{2x+\sqrt{4x^2+2}}=\dfrac{\dfrac{3x}{x^3}}{8+8+8+8}-\dfrac{\dfrac{2}{x}}{2+2}=0\)
5/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2+1-x^2}{\sqrt{x^2+1}+x}+\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-x-x^2}{\sqrt{x^2-x}+x}=\dfrac{\dfrac{1}{x}}{1+1}-\dfrac{\dfrac{x}{x}}{1+1}=-\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
limlimits_{xrightarrow+infty}left(sqrt{x^2+x+1}-sqrt[3]{2x^3+x-1}right)limlimits_{xrightarrow+infty}left(sqrt{4x^2+x+1}-2xright)limlimits_{xrightarrow-infty}left(sqrt[3]{x^3+x^2+1}+sqrt{x^2+x+1}right)limlimits_{xrightarrow+infty}left(sqrt{x^2+x+1}-2sqrt{x^2-x}+xright)limlimits_{xrightarrow+infty}xleft(sqrt{x^2+2x}-2sqrt{x^2+x}+xright)
Đọc tiếp
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+x+1}-\sqrt[3]{2x^3+x-1}\right)\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{4x^2+x+1}-2x\right)\)
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{x^3+x^2+1}+\sqrt{x^2+x+1}\right)\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+x+1}-2\sqrt{x^2-x}+x\right)\)
\(\lim\limits_{x\rightarrow+\infty}x\left(\sqrt{x^2+2x}-2\sqrt{x^2+x}+x\right)\)
1/ \(=\lim\limits_{x\rightarrow+\infty}x\left(\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}-\sqrt[3]{\dfrac{2x^3}{x^3}+\dfrac{x}{x^3}-\dfrac{1}{x^3}}\right)=x\left(1-\sqrt[3]{2}\right)=-\infty\)
2/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{4x^2+x+1-4x^2}{\sqrt{4x^2+x+1}+2x}=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{x}{x}+\dfrac{1}{x}}{\sqrt{\dfrac{4x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}+\dfrac{2x}{x}}=\dfrac{1}{2+2}=\dfrac{1}{4}\)
3/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{x^3+x^2+1-x^3}{\left(\sqrt[3]{x^3+x^2+1}\right)^2+x.\sqrt[3]{x^3+x^2+1}+x^2}+\dfrac{x^2+x+1-x^2}{\sqrt{x^2+x+1}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{x^2}{x^2}+\dfrac{1}{x^2}}{\dfrac{\left(\sqrt[3]{x^3+x^2+1}\right)^2}{x^2}+\dfrac{x}{x^2}\sqrt[3]{x^3+x^2+1}+\dfrac{x^2}{x^2}}+\dfrac{\dfrac{x}{x}+\dfrac{1}{x}}{-\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}-\dfrac{x}{x}}=\dfrac{1}{3}-\dfrac{1}{2}=-\dfrac{1}{6}\)
4/ \(=\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+x+1}-x\right)+\lim\limits_{x\rightarrow+\infty}2\left(x-\sqrt{x^2-x}\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2+x+1-x^2}{\sqrt{x^2+x+1}+x}+\lim\limits_{x\rightarrow+\infty}2.\dfrac{x^2-x^2+x}{x+\sqrt{x^2-x}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{x}{x}+\dfrac{1}{x}}{\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}+\dfrac{x}{x}}+\lim\limits_{x\rightarrow+\infty}2.\dfrac{\dfrac{x}{x}}{\dfrac{x}{x}+\sqrt{\dfrac{x^2}{x^2}-\dfrac{x}{x^2}}}=\dfrac{1}{2}+\dfrac{2}{2}=\dfrac{3}{2}\)
5/ \(=\lim\limits_{x\rightarrow+\infty}x.\left(\dfrac{x^2+2x-x^2}{\sqrt{x^2+2x}+x}+2.\dfrac{x^2-x^2+x}{\sqrt{x^2-x}+x}\right)=+\infty\)
Đúng 1
Bình luận (0)
\(\lim\limits_{x\rightarrow-\infty}\left(3x^3+5x^2-9\sqrt{2}x-2017\right)\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+x+1}-\sqrt[3]{2x^3+x-1}\right)\)
\(\lim\limits_{x\rightarrow-\infty}\left(x-\sqrt{x^2+x+1}\right)\)
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{x^3+x^2+1}+\sqrt{x^2+x+1}\right)\)
a/ \(=\lim\limits_{x\rightarrow-\infty}x^3\left(3+\dfrac{5x^2}{x^3}-\dfrac{9\sqrt{2}x}{x^3}-\dfrac{2017}{x^3}\right)=3.x^3=-\infty\)
b/ \(=\lim\limits_{x\rightarrow+\infty}x\left(\sqrt{1+\dfrac{x}{x^2}+\dfrac{1}{x^2}}-\sqrt[3]{2+\dfrac{x}{x^3}-\dfrac{1}{x^3}}\right)=\left(1-\sqrt[3]{2}\right)x=-\infty\)
c/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2-x^2-x-1}{x+\sqrt{x^2+x+1}}=\lim\limits_{x\rightarrow-\infty}\dfrac{-\dfrac{x}{x}-\dfrac{1}{x}}{\dfrac{x}{x}-\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}}=-\dfrac{1}{1-1}=-\infty\)
d/ \(=\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{x^3+x^2+1}-x\right)+\lim\limits_{x\rightarrow-\infty}\left(x+\sqrt{x^2+x+1}\right)\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{x^3+x^2+1-x^3}{\left(\sqrt[3]{x^3+x^2+1}\right)^2+x\sqrt[3]{x^3+x^2+1}-x^2}+\lim\limits_{x\rightarrow-\infty}\dfrac{x^2-x^2-x-1}{x-\sqrt{x^2+x+1}}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2+1}{\left(-x\sqrt[3]{\dfrac{x^3}{x^3}+\dfrac{x^2}{x^3}+\dfrac{1}{x^3}}\right)^2-x.x\sqrt[3]{\dfrac{x^3}{x^3}+\dfrac{x^2}{x^3}+\dfrac{1}{x^3}}-x^2}+\lim\limits_{x\rightarrow-\infty}\dfrac{-x-1}{x+x\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}}\)
\(=\dfrac{1}{1-1-1}+\dfrac{-1}{1+1}=-1-\dfrac{1}{2}=-\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2-x+1}-x\right)\)
\(\lim\limits_{x\rightarrow-\infty}x\left(\sqrt{4x^2+1}-x\right)\)
\(\lim\limits_{x\rightarrow-\infty}\left(4x^5-3x^3+x+1\right)\)
\(\lim\limits_{x\rightarrow+\infty}\sqrt{x^4-x^3+x^2-x}\)
Hic nan qua :( Lam vay
P/s: Anh Lam check all ho em nhung bai em lam nhe :( Em cam on
1/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-x+1-x^2}{\sqrt{x^2-x+1}+x}=\dfrac{-1}{1+1}=-\dfrac{1}{2}\)
2/ \(=\lim\limits_{x\rightarrow-\infty}x\left(\dfrac{4x^2+1-x^2}{\sqrt{4x^2+1}+x}\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{x}{x}}{-\sqrt{\dfrac{4x^2}{x^2}+\dfrac{1}{x^2}}+\dfrac{x}{x}}=\dfrac{1}{-2+1}=-1\)
3/ \(=\lim\limits_{x\rightarrow-\infty}x^5\left(4-\dfrac{3}{x^2}+\dfrac{1}{x^4}+\dfrac{1}{x^5}\right)=-\infty\)
4/ \(=\lim\limits_{x\rightarrow+\infty}\sqrt{x^4}\left(\sqrt{1-\dfrac{x^3}{x^4}+\dfrac{x^2}{x^4}-\dfrac{x}{x^4}}\right)=+\infty\)
Đúng 1
Bình luận (0)
Tính các giới hạn sau:
a) \(\lim\limits_{x\rightarrow0^-}\dfrac{2\left|x\right|+x}{x^2-x}\)
b) \(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2-x}-\sqrt{x^2-1}\right)\)
c) \(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt[3]{1+x^4+x^6}}{\sqrt{1+x^3+x^4}}\)
a: \(\lim\limits_{x->0^-^-}\dfrac{-2x+x}{x\left(x-1\right)}=lim_{x->0^-}\left(\dfrac{-x}{x\left(x-1\right)}\right)\)
\(=lim_{x->0^-}\left(\dfrac{-1}{x-1}\right)=\dfrac{-1}{0-1}=\dfrac{-1}{-1}=1\)
b: \(=lim_{x->-\infty}\left(\dfrac{x^2-x-x^2+1}{\sqrt{x^2-x}+\sqrt{x^2-1}}\right)\)
\(=lim_{x->-\infty}\left(\dfrac{-x+1}{\sqrt{x^2-x}+\sqrt{x^2-1}}\right)\)
\(=lim_{x->-\infty}\left(\dfrac{-1+\dfrac{1}{x}}{-\sqrt{1-\dfrac{1}{x^2}}-\sqrt{1-\dfrac{1}{x^2}}}\right)=\dfrac{-1}{-2}=\dfrac{1}{2}\)
Đúng 0
Bình luận (1)
Tính các giới hạn :
a) limlimits_{xrightarrow+infty}left(dfrac{x^3}{3x^2-4}-dfrac{x^2}{3x+2}right)
b) limlimits_{xrightarrow+infty}left(sqrt{9x^2+1}-3xright)
c) limlimits_{xrightarrow-infty}left(sqrt{2x^2-3}-5xright)
d) limlimits_{xrightarrow+infty}dfrac{sqrt{2x^2+3}}{4x+2}
e) limlimits_{xrightarrow-infty}dfrac{sqrt{2x^2+3}}{4x+2}
Đọc tiếp
Tính các giới hạn :
a) \(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{x^3}{3x^2-4}-\dfrac{x^2}{3x+2}\right)\)
b) \(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{9x^2+1}-3x\right)\)
c) \(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{2x^2-3}-5x\right)\)
d) \(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{2x^2+3}}{4x+2}\)e) \(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{2x^2+3}}{4x+2}\)
Tính :
a) \(\lim\limits_{x\rightarrow+\infty}\left(x^4-x^2+x-1\right)\)
b) \(\lim\limits_{x\rightarrow-\infty}\left(-2x^3+3x^2-5\right)\)
c) \(\lim\limits_{x\rightarrow-\infty}\sqrt{x^2-2x+5}\)
d) \(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}+x}{5-2x}\)
a)  (x4 – x2 + x - 1) =
(x4 – x2 + x - 1) =  x4(1 -
x4(1 - 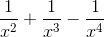 ) = +∞.
) = +∞.
b)  (-2x3 + 3x2 -5 ) =
(-2x3 + 3x2 -5 ) =  x3(-2 +
x3(-2 + 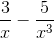 ) = +∞.
) = +∞.
c) 
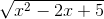 =
= 
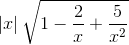 = +∞.
= +∞.
d) \(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}+x}{5-2x}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left|x\right|\sqrt{1+\dfrac{1}{x^2}}+x}{5-2x}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{x\sqrt{1+\dfrac{1}{x^2}}+x}{5-2x}\)\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{1+\dfrac{1}{x^2}}+1}{\dfrac{5}{x}-2}=-1\).
Đúng 0
Bình luận (0)




