Tìm x,y biết
(2x-5)2023+(3y+4)2024≤0
(2x + 4) mũ 2024 + I 3y - 9 I mũ 2023 = 0. tìm x và y. nhanh nhé .mk đang cần gấp😊😊
\(\left(2x+4\right)^{2024}+\left(\left|3y-9\right|\right)^{2023}=0\) (*)
Ta có: \(\left(2x+4\right)^{2024}\ge0\forall x\) (vì có số mũ chẵn) (1)
\(\left(\left|3y-9\right|\right)^{2023}\ge0\forall y\) (vì giá trị tuyệt đối luôn ≥0) (2)
Từ (1) và (2) ta có:
\(\Rightarrow\left\{{}\begin{matrix}2x+4=0\\3y-9=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=3\end{matrix}\right.\)
Vậy: ...
Tìm x , y biết: (2x -5)2022 + (3y +4)2024 ≤ 0
Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
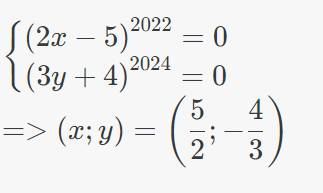 Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
\(\left|x-3y\right|^{2023}+\left|y+4\right|^{2024}=0\)
Vì `{(|x - 3y|^2023 >=0), (|y+4|^2024 >=0):} forall x, y`
Nên `{(x=3y), (y = -4):}`
`<=> {(x=-12), (y=-4):}`
=>x-3y=0 và y+4=0
=>y=-4 và x=3y=-12
|x-3y|^2023 + |y+4|^2024 = 0
⇒|x-3y| = 0 và |y+4| = 0
⇒x- 3y=0 và y+4 = 0
y = -4
Vậy, nghiệm của phương trình |x-3y|^2023 + |y+4|^2024 = 0 là x - 3y = 0 và y = -4.
Tìm xEZ, biết
a) 7x .(2x+10)=0
b)-9x:(2x-10)=0
c) (4-x) (x+3)=0
d) (x+2023) . (x - 2024)=0
a, 7\(x\).(2\(x\) + 10) =0
\(\left[{}\begin{matrix}x=0\\2x+10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\2x=-10\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy \(x\in\) {-5; 0}
b, -9\(x\) : (2\(x\) - 10) = 0
9\(x\) = 0
\(x\) = 0
c, (4 - \(x\)).(\(x\) + 3) = 0
\(\left[{}\begin{matrix}4-x=0\\x+3=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy \(x\in\) {-3; 4}
d, (\(x\) + 2023).(\(x\) - 2024) = 0
\(\left[{}\begin{matrix}x+2023=0\\x-2024=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-2023\\x=2024\end{matrix}\right.\)
Vậy \(x\in\) {-2023; 2024}
Tìm x,y biết: (x+1)^2024+(căn hai y-1)^2023=0
ĐKXĐ: y>=0
\(\left(x+1\right)^{2024}>=0\forall x\)
\(\left(\sqrt{y-1}\right)^{2023}>=0\forall y\) thỏa mãn ĐKXĐ
=>\(\left(x+1\right)^{2024}+\left(\sqrt{y-1}\right)^{2023}>=0\forall x,y\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+1=0\\y-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Tìm số nguyên dương x sao cho 5x +13 là bội của 2x+1
Tìm x biết (2x-18).(3x+12)=0
Tính S= 1-2-3+4+
5-6-7+8+...+2021-2022-2023+2024+2025
1. Giải:
Do \(5x+13B\in\left(2x+1\right)\Rightarrow5x+13⋮2x+1.\)
\(\Rightarrow2\left(5x+13\right)⋮2x+1\Rightarrow10x+26⋮2x+1.\)
\(\Rightarrow5\left(2x+1\right)+21⋮2x+1.\)
Do 5(2x+1)⋮2x+1⇒ Ta cần 21⋮2x+1.
⇒ 2x+1 ϵ B(21)=\(\left\{1;3;7;21\right\}.\)
Ta có bảng:
| 2x+1 | 1 | 3 | 7 | 21 |
| x | 0 | 1 | 3 | 10 |
| TM | TM | TM | TM |
Vậy xϵ\(\left\{0;1;3;10\right\}.\)
2. Giải:
Do (2x-18).(3x+12)=0.
⇒ 2x-18=0 hoặc 3x+12=0.
⇒ 2x =18 3x =-12.
⇒ x =9 x =-4.
Vậy xϵ\(\left\{-4;9\right\}.\)
3. S= 1-2-3+4+5-6-7+8+...+2021-2022-2023+2024+2025.
S= (1-2-3+4)+(5-6-7+8)+...+(2021-2022-2023+2024)+2025 Có 506 cặp.
S= 0 + 0 + ... + 0 + 2025.
⇒S= 2025.
Tìm x,y biết: (x−2)2024 + (√y−2)2023 = 0.(trình bày từng bước )\
Mong trả lời
a) 7x .(2x+10)=0
b)-9x:(2x-10)=0
c) (4-x) (x+3)=0
d) (x+2023) . (x - 2024)=0
a, 7\(x\).(2\(x\) + 10) = 0
\(\left[{}\begin{matrix}x=0\\2x+10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\2x=-10\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-10:2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy \(x\in\){-5; 0}
b, - 9\(x\) : (2\(x\) - 10) = 0
- 9\(x\) = 0
\(x\) = 0
c, (4 - \(x\)).(\(x\) + 3) = 0
\(\left[{}\begin{matrix}4-x=0\\x+3=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy \(x\in\) {-3; 4}
d, (\(x\) + 2023).(\(x\) - 2024) = 0
\(\left[{}\begin{matrix}x+2023=0\\x-2024=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-2023\\x=2024\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-2023; 2024}
Cho số s.y thỏa mãn đẳng thức: 5x2+5x2+8xy-2x+2y+2=0. tính giá trị của biểu thức M=(x-y)2023-(x-2)2024+(y+1)2023.
Sửa đề: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(\left(2x+2y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\left\{{}\begin{matrix}2x+2y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(M=\left(x-y\right)^{2023}-\left(x-2\right)^{2024}+\left(y+1\right)^{2023}\)
\(=\left(1+1\right)^{2023}-\left(1-2\right)^{2024}+\left(-1+1\right)^{2023}\)
\(=2^{2023}-1\)