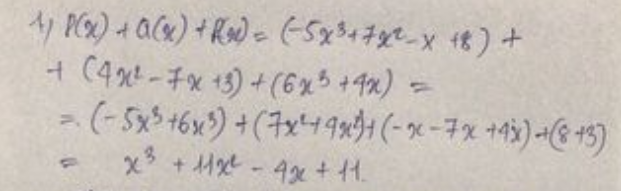x^2 – 7x — 8
H24
Những câu hỏi liên quan
P(x)+Q(x)+R(x)=(-5x mũ 3 + 7x mũ 2 -x + 8) +(4x mũ 2 -7x+3)
Rút gọn rồi tính A vs x =2
A=(7x−8).(7x+8)−10.(2x+3)^2+5x.(3x−2)^2−4x.(x−5)^2
x2 - 7x+ \(\sqrt{x^2-7x+8}\)=12
Đặt \(\sqrt{x^2+7x+8}=t\left(t\ge0\right)\)
Đúng 1
Bình luận (0)
\((2x+3)\left(\dfrac{3x+8}{2-7x}+1\right)=(x-5)\left(\dfrac{3x+8}{2-7x}+1\right)\)
ĐK: ` x \ne 2/7`
`(2x+3)((3x+8)/(2-7x)+1)=(x-5)((3x+8)/(2-7x)+1)`
`<=> ((3x+8)(2-7x)+1)(2x+3-x+5)=0`
`<=> ((3x+8)/(2-7x)+1)(x+8)=0`
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{3x+8}{2-7x}=-1\\x+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-8\end{matrix}\right.\)
Vậy `S={5/2 ; -8}`.
Đúng 2
Bình luận (4)
Giải phương trình sau:
a) x+3/x+1 + x-2/x = 2
b) 3x-2/x+7 = 6x+1/2x-3
c) 5/3x+2 = 2x-1
d) (2x+3) . (3x+8/2-7x + 1) = (x-5) . (3x+8/2-7x + 1)
Xem chi tiết
a) ĐKXĐ: \(x\notin\left\{-1;0\right\}\)
Ta có: \(\dfrac{x+3}{x+1}+\dfrac{x-2}{x}=2\)
\(\Leftrightarrow\dfrac{x\left(x+3\right)}{x\left(x+1\right)}+\dfrac{\left(x+1\right)\left(x-2\right)}{x\left(x+1\right)}=\dfrac{2x\left(x+1\right)}{x\left(x+1\right)}\)
Suy ra: \(x^2+3x+x^2-3x+2=2x^2+2x\)
\(\Leftrightarrow2x^2+2-2x^2-2x=0\)
\(\Leftrightarrow-2x+2=0\)
\(\Leftrightarrow-2x=-2\)
hay x=1(nhận)
Vậy: S={1}
b) ĐKXĐ: \(x\notin\left\{-7;\dfrac{3}{2}\right\}\)
Ta có: \(\dfrac{3x-2}{x+7}=\dfrac{6x+1}{2x-3}\)
\(\Leftrightarrow\left(3x-2\right)\left(2x-3\right)=\left(6x+1\right)\left(x+7\right)\)
\(\Leftrightarrow6x^2-9x-4x+6=6x^2+42x+x+7\)
\(\Leftrightarrow6x^2-13x+6-6x^2-43x-7=0\)
\(\Leftrightarrow-56x-1=0\)
\(\Leftrightarrow-56x=1\)
hay \(x=-\dfrac{1}{56}\)(nhận)
Vậy: \(S=\left\{-\dfrac{1}{56}\right\}\)
c) ĐKXĐ: \(x\ne-\dfrac{2}{3}\)
Ta có: \(\dfrac{5}{3x+2}=2x-1\)
\(\Leftrightarrow5=\left(3x+2\right)\left(2x-1\right)\)
\(\Leftrightarrow6x^2-3x+4x-2-5=0\)
\(\Leftrightarrow6x^2+x-7=0\)
\(\Leftrightarrow6x^2-6x+7x-7=0\)
\(\Leftrightarrow6x\left(x-1\right)+7\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(6x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\6x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\6x=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-\dfrac{7}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{1;-\dfrac{7}{6}\right\}\)
d) ĐKXĐ: \(x\ne\dfrac{2}{7}\)
Ta có: \(\left(2x+3\right)\cdot\left(\dfrac{3x+8}{2-7x}+1\right)=\left(x-5\right)\left(\dfrac{3x+8}{2-7x}+1\right)\)
\(\Leftrightarrow\left(2x+3\right)\cdot\left(\dfrac{3x+8+2-7x}{2-7x}\right)-\left(x-5\right)\left(\dfrac{3x+8+2-7x}{2-7x}\right)=0\)
\(\Leftrightarrow\left(2x+3-x+5\right)\cdot\dfrac{-4x+6}{2-7x}=0\)
\(\Leftrightarrow\left(x+8\right)\cdot\left(-4x+6\right)=0\)(Vì \(2-7x\ne0\forall x\) thỏa mãn ĐKXĐ)
\(\Leftrightarrow\left[{}\begin{matrix}x+8=0\\-4x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\-4x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\left(nhận\right)\\x=\dfrac{3}{2}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{-8;\dfrac{3}{2}\right\}\)
Đúng 1
Bình luận (0)
Giải các phương trình sau:
a) \(\dfrac{7x-3}{x-1}=\dfrac{2}{3}\).
b) \(\dfrac{2\left(3-7x\right)}{1+x}=\dfrac{1}{2}\).
c) \(\dfrac{1}{x-2}+3=\dfrac{3-x}{x-2}\).
d) \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\).
a) ĐKXĐ: \(x\ne1\)
Ta có: \(\dfrac{7x-3}{x-1}=\dfrac{2}{3}\)
\(\Leftrightarrow3\left(7x-3\right)=2\left(x-1\right)\)
\(\Leftrightarrow21x-9=2x-2\)
\(\Leftrightarrow21x-2x=-2+9\)
\(\Leftrightarrow19x=7\)
\(\Leftrightarrow x=\dfrac{7}{19}\)
Vậy: \(S=\left\{\dfrac{7}{19}\right\}\)
Đúng 1
Bình luận (0)
x2 - 7x + \(\sqrt{x^2-7x+8}=12\)
\(x^2-7x+\sqrt{x^2-7x+8}=12\)
\(x^2-7x-12+\sqrt{x^2-7x+8}=0\)
\(x^2-7x+8-20+\sqrt{x^2-7x+8}=0\)
Đặt : \(\sqrt{x^2-7x+8}=t\left(đk:t>0\right)\)
\(\Rightarrow x^2-7x+8=t^2\)
\(\Rightarrow\)Phương trình trở thành : \(t^2+t-20=0\)
\(\Rightarrow\orbr{\begin{cases}t=4\left(tm\right)\\t=-5\left(L\right)\end{cases}}\)
Với \(t=4\Rightarrow\sqrt{x^2-7x+8}=4\)
\(\Rightarrow x^2-7x+8=16\)
\(\Rightarrow x^2-7x+8-16=0\)
\(\Rightarrow x^2-7x-8=0\)
\(\Rightarrow\orbr{\begin{cases}x=8\\x=-1\end{cases}}\)
Đúng 0
Bình luận (0)
\(x^2-7x+\sqrt{x^2-7x+8}=12\)
\(\Leftrightarrow\sqrt{x^2-7x+8}=12-x^2+7x\)
\(\Leftrightarrow\sqrt{x^2-7x+8}-4=8-x^2+7x\)
\(\Leftrightarrow\frac{x^2-7x+8-16}{\sqrt{x^2-7x+8}+4}=-\left(x-8\right)\left(x+1\right)\)
\(\Leftrightarrow\frac{\left(x-8\right)\left(x+1\right)}{\sqrt{x^2-7x+8}+4}+\left(x-8\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+1\right)\left(\frac{1}{\sqrt{x^2-7x+8}+4}+1\right)=0\)
Dễ thấy: \(\frac{1}{\sqrt{x^2-7x+8}+4}+1>0\)
\(\Rightarrow\orbr{\begin{cases}x-8=0\\x+1=0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=8\\x=-1\end{cases}}\)
Đúng 0
Bình luận (0)
P(x)=-5x^3+7x^2-x+3 Q(x)=4x^2+7x-8 .Tính Q(x)+P(x) Q(x)-P(x)
câu 1: x^2-5x+4=0
câu 2 : 3x^2-7x+3=0
câu 3 : 5x^2-x-4=0
câu 4: 7x^2+x-8=0
cảm ơn nha ![]()
Câu 1:
Ta có: \(x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-4x+4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
Vậy: S={1;4}
Câu 2:
Ta có: \(3x^2-7x+3=0\)
\(\Delta=\left(-7\right)^2-4\cdot3\cdot3=49-36=13\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{7-\sqrt{13}}{6}\\x_2=\dfrac{7+\sqrt{13}}{6}\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{7-\sqrt{13}}{6};\dfrac{7+\sqrt{13}}{6}\right\}\)
Câu 3:
Ta có: \(5x^2-x-4=0\)
\(\Leftrightarrow\left(x-1\right)\left(5x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Vậy: \(S=\left\{1;-\dfrac{4}{5}\right\}\)
Câu 4:
Ta có: \(7x^2+x-8=0\)
\(\Leftrightarrow\left(x-1\right)\left(7x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{8}{7}\end{matrix}\right.\)
Vậy: \(S=\left\{1;-\dfrac{8}{7}\right\}\)
Đúng 2
Bình luận (2)
Câu 1x^2-5x+4=0
<=>(x-1)(x-4)=0
<=>[x=1;x=4
Câu 2 3x^2-7x+3=0
x=7/6-căn bậc hai(13)/6, x=căn bậc hai(13)/6+7/6
x=7/6-căn bậc hai(13)/6, x=căn bậc hai(13)/6+7/6
Câu 3 5*x^2 -x-4 = 0
x=-4/5, x=1
Câu 4 7*x^2 +x-8 = 0
x=-8/7, x=1
bn ơi mk giải thế có chỗ nào ko hiểu bn có thể hỏi mk nhé
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
a, 2x^2+3x-27
b, x^2-7x-6
c, x^2+7x+12
d,x^2-10x+16
e,x^2-8x+15
g,x^2+6x+8
a) \(2x^2+3x-27\)
\(=2x^2+9x-6x-27\)
\(=x\left(2x+9\right)-3\left(2x+9\right)\)
\(=\left(2x+9\right)\left(x-3\right)\)
b) sửa đề thành \(x^2+7x+6\)
\(x^2+7x+6\)
\(=x^2+x+6x+6\)
\(=x\left(x+1\right)+6\left(x+1\right)\)
\(=\left(x+1\right)\left(x+6\right)\)
Đúng 0
Bình luận (0)