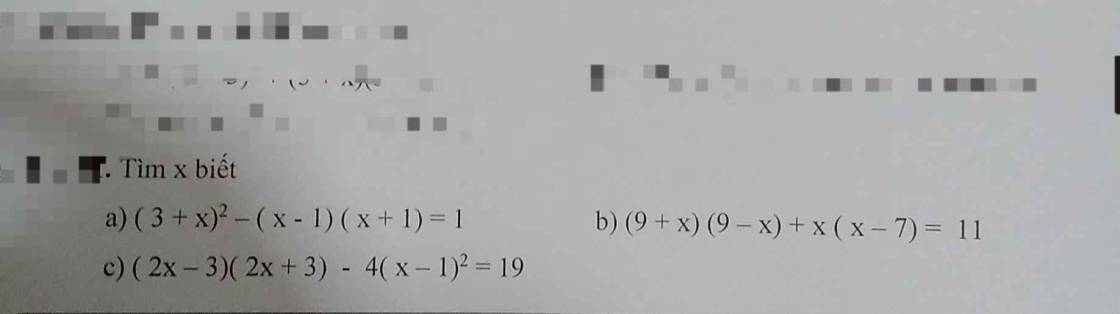 chi tiêttiết
chi tiêttiết
HT
Những câu hỏi liên quan
 chi tiêttiết
chi tiêttiết
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
Xét ΔIBC có
IH vừa là đường cao, vừalà trung tuyến
=>ΔIBC cân tại I
c: Xét ΔMAB và ΔMCE có
góc MAB=góc MCE
MA=MC
góc AMB=góc CME
=>ΔMAB=ΔMCE
=>AB=CE=CA
Đúng 1
Bình luận (0)
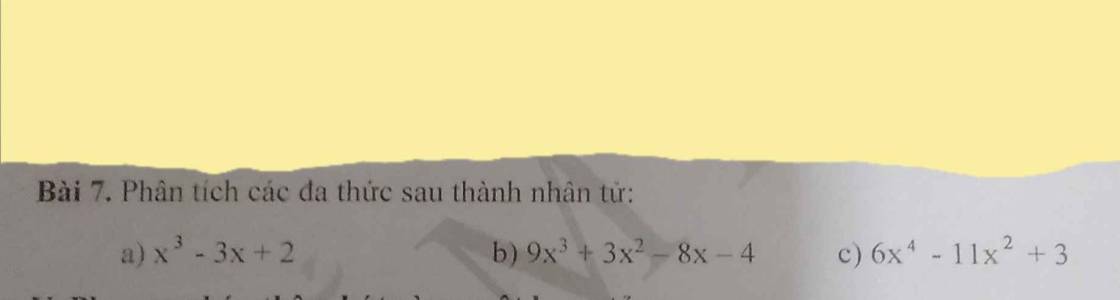 hi tiêttiết
hi tiêttiết
a: \(x^3-3x+2\)
\(=x^3-x-2x+2\)
\(=\left(x^3-x\right)-\left(2x-2\right)\)
\(=x\left(x^2-1\right)-2\left(x-1\right)\)
\(=x\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x-2\right)\)
\(=\left(x-1\right)\left(x^2+2x-x-2\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x-1\right)\)
\(=\left(x+2\right)\cdot\left(x-1\right)^2\)
b: \(9x^3+3x^2-8x-4\)
\(=9x^3-9x^2+12x^2-12x+4x-4\)
\(=9x^2\left(x-1\right)+12x\left(x-4\right)+4\left(x-1\right)\)
\(=\left(x-1\right)\left(9x^2+12x+4\right)\)
\(=\left(x-1\right)\left(3x+2\right)^2\)
c: \(6x^4-11x^2+3\)
\(=6x^4-9x^2-2x^2+3\)
\(=3x^2\left(2x^2-3\right)-\left(2x^2-3\right)\)
\(=\left(2x^2-3\right)\left(3x^2-1\right)\)
Đúng 2
Bình luận (0)
\(a,x^3-3x+2\\=x^3-x-2x+2\\=x(x^2-1)-2(x-1)\\=x(x-1)(x+1)-2(x-1)\\=(x-1)[x(x+1)-2]\\=(x-1)(x^2+x-2)\\=(x-1)(x^2-x+2x-2)\\=(x-1)[x(x-1)+2(x-1)]\\=(x-1)^2(x+2)\)
\(b,9x^3+3x^2-8x-4\\=9x^3-9x^2+12x^2-12x+4x-4\\=9x^2(x-1)+12x(x-1)+4(x-1)\\=(x-1)(9x^2+12x+4)\\=(x-1)[(3x)^2+2\cdot 3x\cdot2+2^2]\\=(x-1)(3x+2)^2\)
\(c,6x^4-11x^2+3\\=6x^4-2x^2-9x^2+3\\=2x^2(3x^2-1)-3(3x^2-1)\\=(3x^2-1)(2x^2-3)\\\text{#}Toru\)
Đúng 2
Bình luận (0)
`#3107.101107`
`7.`
`a)`
`x^3 - 3x + 2`
`= x^3 - 2x - x + 2`
`= (x^3 - x) - (2x - 2)`
`= x(x^2 - 1) - 2(x - 1)`
`= x(x - 1)(x + 1) - 2(x - 1)`
`= [ x(x + 1) - 2](x - 1)`
`= (x^2 + x - 2)(x - 1)`
`= (x - 1)(x + 2)(x - 1)`
`= (x - 1)^2 (x + 2)`
`b)`
`9x^3 + 3x^2 - 8x - 4`
`= 9x^3 + 12x^2 - 9x^2 + 4x - 12x - 4`
`= (9x^3 + 12x^2 + 4x) - (9x^2 + 12x + 4)`
`= x(9x^2 + 12x + 4) - (9x^2 + 12x + 4)`
`= (x - 1)(9x^2 + 12x + 4)`
`= (x - 1)(3x + 2)^2`
`c)`
`6x^4 - 11x^2 + 3`
`= 6x^4 - 2x^2 - 9x^2 + 3`
`= (6x^4 - 2x^2) - (9x^2 - 3)`
`= 2x^2(3x^2 - 1) - 3(3x^2 - 1)`
`= (2x^2 - 3)(3x^2 - 1)`
Đúng 3
Bình luận (0)
 chichi tiêttiết
chichi tiêttiết
a) \(x^2+5x-6\)
\(=x^2-x+6x-6\)
\(=\left(x^2-x\right)+\left(6x-6\right)\)
\(=x\left(x-1\right)-6\left(x-1\right)\)
\(=\left(x-1\right)\left(x-6\right)\)
b) \(a^2+4a+3\)
\(=a^2+a+3a+3\)
\(=\left(a^2+a\right)+\left(3a+3\right)\)
\(=a\left(a+1\right)+3\left(a+1\right)\)
\(=\left(a+1\right)\left(a+3\right)\)
c) \(16y-5y^2-3\)
\(=-5y^2+y+15y-3\)
\(=\left(-5y^2+y\right)+\left(15y-3\right)\)
\(=-y\left(5y-1\right)+3\left(5y-1\right)\)
\(=\left(5y-1\right)\left(3-y\right)\)
Đúng 2
Bình luận (0)
a: \(x^2+5x-6\)
\(=x^2+6x-x-6\)
\(=x\left(x+6\right)-\left(x+6\right)\)
\(=\left(x+6\right)\left(x-1\right)\)
b: \(a^2+4a+3\)
\(=a^2+a+3a+3\)
\(=a\left(a+1\right)+3\left(a+1\right)\)
\(=\left(a+1\right)\left(a+3\right)\)
c: \(16y-5y^2-3\)
\(=-5y^2+15y+y-3\)
\(=-5y\cdot\left(y-3\right)+\left(y-3\right)\)
\(=\left(y-3\right)\left(-5y+1\right)\)
Đúng 2
Bình luận (0)
Cây chi chi trên rừng ko lá?
Cá chi chi dưới biển ko xương?
Con chi chi dưới mương ko vảy?
Con chi chi ở bụi trảy ko vi?
Xem thêm câu trả lời
Chứng minh Rằng
\(\frac{sin^2\chi+cos^2\chi+cos^4\chi}{cos^2\chi-sin^2\chi+sin^4\chi}=tan^4\chi\)
giúp mik nha .mik cần rất gấp
Sửa đề
\(\frac{sin^2x-c\text{os}^2x+c\text{os}^4x}{c\text{os}^2x-sin^2x+sin^4x}=\frac{sin^2x-c\text{os}^2x+\left(1-sin^2x\right)^2}{c\text{os}^2x-sin^2x+\left(1-c\text{os}^2x\right)^2}\)
\(=\frac{-sin^2x-c\text{os}^2x+sin^4x+1}{-c\text{os}^2x-sin^2x+c\text{os}^4x+1}\)
\(=\frac{-1+sin^4x+1}{-1+c\text{os}^4x+1}=\frac{sin^4x}{c\text{os}^4x}=tan^4x\)
Đúng 0
Bình luận (0)
Chi tiêu nào sau đây thuộc chi tiêu cho các nhu cầu văn hoá tinh thần
A Chi mua quần áo
B Chi mua quà sinh nhật
C Chi mua gạo
D Chi mua nhà
a, A =\(-2\chi^3+3\chi^2+5\) tại \(\chi=\dfrac{1}{2}\);\(\chi^2-1=0\);\(\chi^2=3\chi\)
b, B =\(-3\chi^3\gamma^2+2\chi^2\gamma^3-2\chi\) tại \(\left|\chi\right|=2\);\(\gamma=1\)
a: \(A\left(\dfrac{1}{2}\right)=-2\cdot\dfrac{1}{8}+3\cdot\dfrac{1}{4}+5=\dfrac{11}{2}\)
\(A\left(1\right)=-2+3+5=6\)
\(A\left(-1\right)=2+3+5=10\)
\(A\left(0\right)=-2\cdot0+3\cdot0+5=5\)
\(A\left(-3\right)=-2\cdot\left(-27\right)+3\cdot9+5=86\)
b: Khi x=2 và y=1 thì
\(B=-3\cdot8\cdot1+2\cdot4-2\cdot2=-20\)
Khi x=-2 và y=1 thì
\(B=-3\cdot\left(-8\right)\cdot1+2\cdot4-2\cdot\left(-2\right)=36\)
Đúng 0
Bình luận (0)
\(\dfrac{\chi+1}{\chi+2}-\dfrac{5}{\chi+2}=\dfrac{12}{\chi^2-4}+1\)
Sửa đề: \(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)
ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
Ta có: \(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{5\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}+\dfrac{x^2-4}{\left(x-2\right)\left(x+2\right)}\)
Suy ra: \(x^2+3x+2-5x+10-12-x^2+4=0\)
\(\Leftrightarrow-2x+4=0\)
\(\Leftrightarrow-2x=-4\)
hay x=2(loại)
Vậy: \(S=\varnothing\)
Đúng 0
Bình luận (0)
\(\Leftrightarrow\) \(\dfrac{x+1}{x+2}-\dfrac{5}{x+2}-\dfrac{12}{\left(x+2\right)\left(x-2\right)}-1=0\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{5\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{12}{\left(x+2\right)\left(x-2\right)}-\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=0\) 0
\(\Leftrightarrow x^2+x-2x-2-5x+10-12-x^2+4=0\)\(\Leftrightarrow\)\(-6x=0\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)
Năm nay, chị Chi 16 tuổi. 2 năm nữa, tuổi Chi kém chị 6 tuổi.
a, Hỏi năm nay, Chi bao nhiêu tuổi?
b, Hỏi 10 năm sau, tổng số tuổi của chị Chi và Chi là bao nhiêu?
c, Hỏi năm nay, chị Chi hơn Chi bao nhiêu tuổi?
a,2 năm nữa chi của chi có số tuổi là
16+2 = 18 tuổi
tuổi của chi sau 2 năm nữa là
18-6=12 tuổi
năm nay chi có số tuổi là
12-2 =10 tuổi
b, 10 năm nữa chị chi số tuổi là
16+10=26 tuổi
10 năm nữa chi có số tuổi là
10+10=20 tuổi
vậy 10 năm sau tổng số tuổi của chi và chị của chi là
26+20=46 tuổi
c, năm nay chị chi hơn chi số tuổi là
16-10= 6 tuổi
Đúng 0
Bình luận (0)





