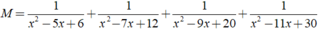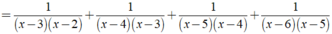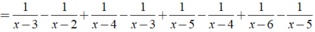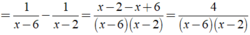11x - 20 < 4 + 5x
MN
Những câu hỏi liên quan
Bài:Chia 1 biến đã sắp xếp 1)(2x^3+11x^2+18x-3):(2x+3) 2)(2x^3+11x^2+18x-3):(3x+3) 3)(2x^3+9x^2+5x+41):(2x^2-x+9) 4)(13x+41x^2+35x^3-14):(5x-2) 5)(5x^2-3x^3+15-9x):(5-3x) 6)(-4x^2+x^3-20+5x):(x-4)
1: \(\dfrac{2x^3+11x^2+18x-3}{2x+3}\)
\(=\dfrac{2x^3+3x^2+8x^2+12x+6x+9-12}{2x+3}\)
\(=x^2+4x+3-\dfrac{12}{2x+3}\)
Đúng 0
Bình luận (0)
Mọi ng lm hộ mih nhé, giải pt:
1) \(\dfrac{5x-150}{50}+\dfrac{5x-102}{49}+\dfrac{5x-56}{48}+\dfrac{5x-12}{47}+\dfrac{5x-60}{46}=0\)
2) (x2 + 11x + 12)(x2 + 9x + 20)(x2 + 13x + 42) = 36(x2 + 11x + 30)(x2 + 11x + 31)
3) 6x4 - 11x3 + 3x2 + 11x - 6x2 + 3 = 0
1) 7x.497902) 2x.41283) 3x-124.54) 3x+15425) 4.2x-31256) 5x515:537) 4x415:168) 7x720:7109) 11x1111:1110) 315.3x33011) 10+2x45:4312) 20+5x55:5313) 4x-2025:2214) 15+2x380:377Chu y: dau . la dau nhan.
Đọc tiếp
1) 7x.49=790
2) 2x.4=128
3) 3x-1=24.5
4) 3x+15=42
5) 4.2x-3=125
6) 5x=515:53
7) 4x=415:16
8) 7x=720:710
9) 11x=1111:11
10) 315.3x=330
11) 10+2x=45:43
12) 20+5x=55:53
13) 4x-20=25:22
14) 15+2x=380:377
Chu y: dau "." la dau nhan.
Mình làm 5 câu thôi nhé !:
1) \(7^x\cdot49=7^{90}\)
\(\Rightarrow7^x\cdot7^2=7^{90}\)
\(\Rightarrow7^{x+2}=7^{90}\)
\(\Rightarrow x=90-2\)
\(\Rightarrow x=88\)
2) \(2^x\cdot4=128\)
\(\Rightarrow2^x\cdot2^2=2^7\)
\(\Rightarrow2^{x+2}=2^7\)
\(\Rightarrow x=7-2\)
\(\Rightarrow x=5\)
3) \(3^x-1=2^4\cdot5\)
\(\Rightarrow3^x=80+1\)
\(\Rightarrow3^x=81\)
\(\Rightarrow3^x=3^4\)
\(\Rightarrow x=4\)
4) \(3^x+15=42\)
\(\Rightarrow3^x=42-15\)
\(\Rightarrow3^x=27\)
\(\Rightarrow3^x=3^3\)
\(\Rightarrow x=3\)
5) \(4\cdot2^x-3=125\)
\(\Rightarrow2^2\cdot2^x=128\)
\(\Rightarrow2^{x+2}=2^7\)
\(\Rightarrow x=7-2\)
\(\Rightarrow x=5\)
Đúng 1
Bình luận (0)
6)
\(5^x=5^{15}:5^3\\ \Leftrightarrow5^x=5^{15-3}\\ \Leftrightarrow5^x=5^{12}\\ \Leftrightarrow x=12\)
7)
\(4^x=4^{15}:16\\ \Leftrightarrow4^x=4^{15}:4^2\\ \Leftrightarrow4^x=4^{15-2}\\ 4^x=4^{13}\\ \Leftrightarrow x=13\)
8)
\(7^x=7^{20}:7^{10}\\ \Leftrightarrow7^x=7^{20-10}\\ \Leftrightarrow7^x=7^{10}\\ \Leftrightarrow x=10\)
9)
\(11^x=11^{11}:11\\ \Leftrightarrow11^x=11^{11-1}\\ \Leftrightarrow11^x=11^{10}\\ \Leftrightarrow x=10\)
10)
\(3^{15}.3^x=3^{30}\\ \Leftrightarrow3^x=3^{30}:3^{15}\\ 3^x=3^{30-15}\\ \Leftrightarrow3^x=3^{15}\\ \Leftrightarrow x=15\)
Đúng 1
Bình luận (0)
11)
\(10+2x=4^5:4^3\\ \Leftrightarrow10+2x=4^2\\ \Leftrightarrow2x=6\\ \Leftrightarrow x=3\)
12)
\(20+5x=5^5:5^3\\ \Leftrightarrow20+5x=5^2\\ \Leftrightarrow5x=5\\ \Leftrightarrow x=1\)
13)
\(4x-20=2^5:2^2\\ \Leftrightarrow4x-20=2^3\\ \Leftrightarrow4x=28\\ \Leftrightarrow x=12\)
14)
\(15+2x=3^{80}:3^{77}\\ \Leftrightarrow15+2x=3^3\\ \Leftrightarrow2x=12\\ \Leftrightarrow x=6\)
Đúng 1
Bình luận (0)
(2x3+11x2+3x2-5x-20):(2x+3)
Áp dụng để rút gọn biểu thức sau:
M
1
x
2
-
5
x
+
6
+
1
x
2
-
7
x
+
12
+
1
x
2
-
9...
Đọc tiếp
Áp dụng để rút gọn biểu thức sau: M = 1 x 2 - 5 x + 6 + 1 x 2 - 7 x + 12 + 1 x 2 - 9 x + 20 + 1 x 2 - 11 x + 30
Giải phương trình
1) 16-8x=0
2) 7x+14=0
3) 5-2x=0
4) 3x-5=7
5) 8-3x=6
6) 8=11x+6
7)-9+2x=0
8) 7x+2=0
9) 5x-6=6+2x
10) 10+2x=3x-7
11) 5x-3=16-8x
12)-7-5x=8+9x
13) 18-5x=7+3x
14) 9-7x=-4x+3
15) 11-11x=21-5x
16) 2(-7+3x)=5-(x+2)
17) 5(8+3x)+2(3x-8)=0
18) 3(2x-1)-3x+1=0
19)-4(x-3)=6x+(x-3)
20)-5-(x+3)=2-5x
20) -5-(x + 3) = 2 - 5x ⇔ -5 - x - 3 = 2 -5x ⇔ 4x = 10 ⇔ x = \(\frac{5}{2}\)
Vậy...
https://i.imgur.com/PCDykdb.jpg
1) 16 - 8x = 0 ⇔ 8(2 - x) = 0⇔ 2 - x = 0 ⇔ x = 2
Vậy phương trình có nghiệm là x = 2
Xem thêm câu trả lời
Giải các phương trình sau:
1/x2+5x+6 + 1/x2+7x+12 + 1/x2+9x+20 + 1/x2+11x+30 = 1/8
\(\Leftrightarrow\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}+...+\dfrac{1}{\left(x+5\right)\left(x+6\right)}=\dfrac{1}{8}\)
=>\(\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}+...+\dfrac{1}{x+5}-\dfrac{1}{x+6}=\dfrac{1}{8}\)
=>1/x+2-1/x+6=1/8
=>\(\dfrac{x+6-x-2}{\left(x+2\right)\left(x+6\right)}=\dfrac{1}{8}\)
=>x^2+8x+12=32
=>x^2+8x-20=0
=>(x+10)(x-2)=0
=>x=-10 hoặc x=2
Đúng 1
Bình luận (0)
a) 152+11x-12
b)6x2-13x+5
c)x4-14x2+24
d)3x2-11x+6
e)-7x2+11x+6
f)4x2+16x-9
g)-5x2-29x-20
h)4x2-12x-7
Giải theo phương pháp tách hạng tử giúp mình nhé!
b) \(6x^2-13x+5=6x^2-3x-10x+5\)
\(=3x\left(2x-1\right)-5\left(2x-1\right)\)
\(=\left(2x-1\right).\left(3x-5\right)\)
Đúng 0
Bình luận (0)
d) \(3x^2-11x+6=3x^2-9x-2x+6\)
\(=3x\left(x-3\right)-2\left(x-3\right)\)
\(=\left(x-3\right)\left(3x-2\right)\)
e) \(-7x^2+11x+6=-7x^2+14x-3x+6\)
\(=-7x\left(x-2\right)-2\left(x-2\right)\)
\(=\left(x-2\right)\left(-7x-2\right)\)
Đúng 0
Bình luận (0)
\(6x^2-13x+5=6x^2-3x-10x+5\)
\(=3x\left(2x-1\right)-5\left(2x-1\right)\)
\(=\left(2x-1\right).\left(3x-5\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
GIẢI PT:
(1/x^2-5x+6)+(!/x^2-7x+12)+(1/x^2-9x+20)+(1/x^2-11x+30)=1/8
Đk:\(x\ne2;x\ne3;x\ne4;x\ne5;x\ne6\)
\(pt\Leftrightarrow\frac{1}{\left(x-6\right)\left(x-5\right)}+\frac{1}{\left(x-5\right)\left(x-4\right)}+...+\frac{1}{\left(x-3\right)\left(x-2\right)}=\frac{1}{8}\)
\(\Leftrightarrow\frac{1}{x-6}-\frac{1}{x-5}+\frac{1}{x-5}-\frac{1}{x-4}+\frac{1}{x-4}+...+\frac{1}{x-3}-\frac{1}{x-2}=\frac{1}{8}\)
\(\Leftrightarrow\frac{1}{x-6}-\frac{1}{x-2}=\frac{1}{8}\)\(\Leftrightarrow\frac{x-2}{\left(x-6\right)\left(x-2\right)}-\frac{x-6}{\left(x-2\right)\left(x-6\right)}=\frac{1}{8}\)
\(\Leftrightarrow\frac{4}{\left(x-6\right)\left(x-2\right)}=\frac{1}{8}\Leftrightarrow\left(x-2\right)\left(x-6\right)=32\)
\(\Leftrightarrow x^2-8x+12=32\Leftrightarrow x^2-8x-20=0\)
\(\Leftrightarrow\left(x-10\right)\left(x+2\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x=10\\x=-2\end{cases}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời