nay voi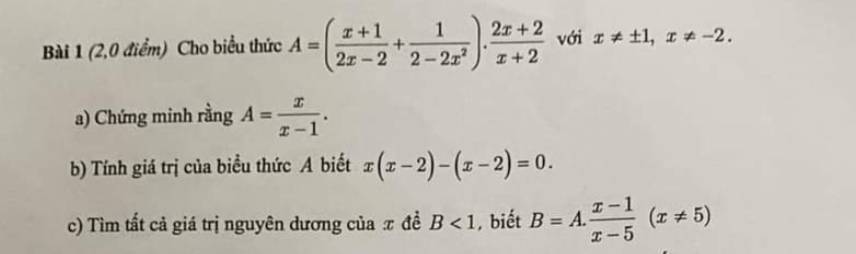
giup minh cau voi
MM
Những câu hỏi liên quan
TBC cua 2 so la 30.Biet St1 gap 4 lan St2. Tim 2 so do
giup minh tra loi cau hoi nay voi ban minh dat thu thach cau hoi minh hong bit cau nay giup minh tra loi cau nay voi bi thua la danh sml lun.
Tổng 2 số: 30*2=60
Số thứ 1: 60/(4+1)*4=48
Số thứ 2: 60-48=12
Vậy St1=48, St2=12
Đúng 0
Bình luận (0)
Tổng 2 số là :
30 x 2 = 60
Ta có sơ đồ :
St1 :|___|___|___|___| tổng : 60
St2 :|___|
Tổng số phần bằng nhau là :
4 + 1 = 5 (phần)
St1 là :
60 : 5 x 4 = 48
St2 là :
60 - 48 = 12
Đ/S : st1 : 48
st2 : 12
Đúng 0
Bình luận (0)
Cho ti le ban do 1:100.000,san truong co dien h. 36m2. Vay dt that cua san truong bao nhieu?
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

giup minh cau nay voi
`1)\sqrt{50}-3\sqrt{8}+\sqrt{32}=5\sqrt{2}-6\sqrt{2}+4\sqrt{2}=3\sqrt{2}`
`2)`
`a)\sqrt{x^2-4x+4}=1`
`<=>\sqrt(x-2)^2}=1`
`<=>|x-2|=1`
`<=>[(x-2=1),(x-2=-1):}<=>[(x=3),(x=1):}`
`b)\sqrt{x^2-3x}-\sqrt{x-3}=0` `ĐK: x >= 3`
`<=>\sqrt{x}\sqrt{x-3}-\sqrt{x-3}=0`
`<=>\sqrt{x-3}(\sqrt{x}-1)=0`
`<=>[(\sqrt{x-3}=0),(\sqrt{x}-1=0):}`
`<=>[(x-3=0),(\sqrt{x}=1):}<=>[(x=3(t//m)),(x=1(ko t//m)):}`
Đúng 0
Bình luận (0)
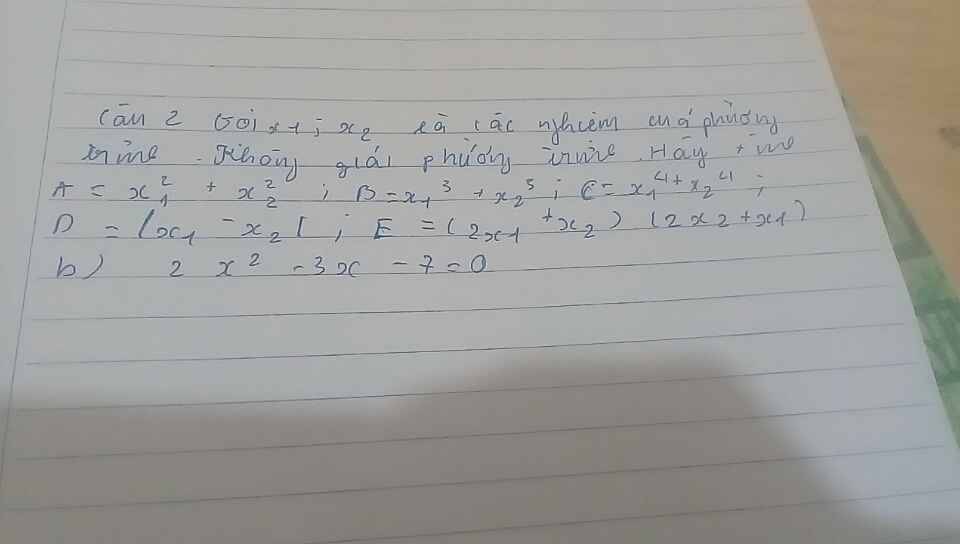
giup minh cau nay voi
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1x_2=-\dfrac{7}{2}\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{37}{4}\)
\(B=x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\dfrac{153}{8}\)
\(C=x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2\left(x_1x_2\right)^2=\dfrac{977}{16}\)
\(D=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\dfrac{\sqrt{65}}{2}\)
\(E=\left(2x_1+x_2\right)\left(2x_2+x_1\right)=2\left(x_1^2+x_2^2\right)+5x_1x_2=1\)
Đúng 2
Bình luận (0)
 giup minh cau nay voi
giup minh cau nay voi
`a,` Đthang đi qua `A(3, 12)`.
`-> x = 3, y = 12 in y`.
`<=> 12 = 9a.`
`<=> a = 12/9 = 4/3.`
`b,` Đthang đi qua `B(-2;3)`.
`=> x = -2, y = 3 in y`.
`<=> 3=4a`.
`<=> a = 3/4`.
Đúng 0
Bình luận (0)

giup minh cau nay voi
`3x^2+10x+3=0`
Ptr có: `\Delta'=5^2-3.3=16 > 0`
`=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=-10/3),(x_1 .x_2=c/a=1):}`
~~~~~~~~~~~~~
`A=x_1 ^2+x_2 ^2`
`A=(x_1+x_2)^2-2x_1 .x_2`
`A=(-10/3)^2-2.1=82/9`
_______________________________________________________
`B=x_1 ^3+x_2 ^3`
`B=(x_1+x_2)(x_1 ^2-x_1 .x_2+x_2 ^2)`
`B=(x_1+x_2)[(x_1+x_2)^2 -3x_1 .x_2]`
`B=(-10/3).[(-10/3)^2-3.1]=-730/27`
_______________________________________________________
`C=x_1 ^4+x_2 ^4`
`C=(x_1 ^2+x_2 ^2)^2 -2x_1 ^2 .x_2 ^2`
`C=[(x_1+x_2)^2-2x_1 .x_2]^2-2(x_1 .x_2)^2`
`C=[(-10/3)^2-2.1]^2-2. 1^2=6562/81`
_______________________________________________________
`D=|x_1-x_2|`
`D=\sqrt{(x_1-x_2)^2}`
`D=\sqrt{(x_1+x_2)^2-4x_1.x_2}`
`D=\sqrt{(-10/3)^2-4.1}=8/3`
_______________________________________________________
`E=(2x_1+x_2)(2x_2+x_1)`
`E=4x_1 .x_2+2x_1 ^2+2x_2 ^2+x_1 .x_2`
`E=5x_1 . x_2+2(x_1+x_2)^2-4x_1 .x_2`
`E=x_1 .x_2+2(x_1+x_2)^2`
`E=1+2(-10/3)^2=209/9`
Đúng 1
Bình luận (0)

giup minh cau nay voi
`a)` Thay `x=-3` vào ptr có:
`(-3)^2-6.(-3)+2m+1=0`
`<=>9+18+2m+1=0`
`<=>m=-14`
`b)` Ptr có: `\Delta'=(-3)^2-(2m+1)=9-2m-1=8-2m`
Ptr có `2` nghiệm phân biệt `<=>\Delta' > 0`
`<=>8-2m > 0<=>m < 4`
`c)` Ptr có nghiệm kép `<=>\Delta' =0`
`<=>8-2m=0<=>m=4`
Đúng 1
Bình luận (0)
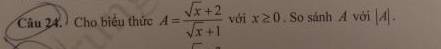
GIUP MINH CAU NAY VOI
\(A=\dfrac{\sqrt{x}+1+1}{\sqrt{x}+1}=1+\dfrac{1}{\sqrt{x}+1}>=1>0\)
=>A>|A|
Đúng 0
Bình luận (0)
Ta có: A= \(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)= \(1+\dfrac{1}{\sqrt{x}+1}\)
Vì x ≥0⇒\(\sqrt{x}\) ≥0⇒\(\sqrt{x}+1 \)≥ 1 ⇒ \(1+\dfrac{1}{\sqrt{x}+1}\)≥ 2
hay A≥ 2>0
Khi đó ta có: A=|A|
Vậy A=|A|
Đúng 0
Bình luận (0)

giup minh cau nay voi
a.
Phương trình hoành độ giao điểm (P) và (d):
\(\dfrac{1}{2}x^2=-\dfrac{3}{2}x+2\Leftrightarrow x^2+3x-4=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=\dfrac{1}{2}\\x=-4\Rightarrow y=8\end{matrix}\right.\)
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ là \(\left(1;\dfrac{1}{2}\right)\) và \(\left(-4;8\right)\)
b.
Phương trình hoành độ giao điểm:
\(\dfrac{1}{2}x^2=mx+2\Leftrightarrow x^2-2mx-4=0\) (1)
\(ac=-4< 0\) nên (1) luôn có 2 nghiệm trái dấu
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-4\end{matrix}\right.\)
Đặt \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4m^2+8\)
Do \(m^2\ge0;\forall m\Rightarrow2m^2+8\ge8;\forall m\)
\(\Rightarrow P_{min}=8\)
Dấu "=" xảy ra khi \(m^2=0\Rightarrow m=0\)
Đúng 1
Bình luận (0)
a: Khi m=-3/2 thì y=-3/2x+2
PTHĐGĐ là:
1/2x^2+3/2x-2=0
=>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1
=>y=1/2*(-4)^2=8 hoặc y=1/2
b: PTHĐGĐ là:
1/2x^2-mx-2=0
=>x^2-2mx-4=0
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(-4\right)=4m^2+16>0\)
=>PT luôn có hai nghiệm phân biệt
x1^2+x2^2
=(x1+x2)^2-2x1x2
=(2m)^2-2*(-4)=4m^2+8>=8
Dấu = xảy ra khi m=0
Đúng 0
Bình luận (0)
 giup minh cau nay voi
giup minh cau nay voi
a. Em tự giải
b.
Phương trình hoành độ giao điểm (P) và (d):
\(-x^2=x+m-1\Leftrightarrow x^2+x+m-1=0\) (1)
(d) cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=1-4\left(m-1\right)>0\Rightarrow m< \dfrac{5}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=m-1\end{matrix}\right.\)
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{4\left(x_1+x_2\right)}{x_1x_2}+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{-4}{m-1}+m-1+3=0\)
\(\Rightarrow-4+\left(m-1\right)\left(m+2\right)=0\) (\(m\ne1\))
\(\Leftrightarrow m^2+m-6=0\Rightarrow\left[{}\begin{matrix}m=2>\dfrac{5}{4}\left(loại\right)\\m=-3\end{matrix}\right.\)
Vậy \(m=-3\)
Đúng 1
Bình luận (0)
a:
b: PTHĐGĐ là:
-x^2=x+m-1
=>-x^2-x-m+1=0
=>x^2+x+m-1=0
\(\Delta=1^2-4\left(m-1\right)=1-4m+4=5-4m\)
Để (P) cắt (d) tại hai điểm phân biệt thì 5-4m>0
=>4m<5
=>m<5/4
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
=>\(4\cdot\dfrac{x_1+x_2}{x_1x_2}+x_1x_2+3=0\)
=>\(4\cdot\dfrac{-1}{m-1}+m-1+3=0\)
=>-4+(m-1)^2+3(m-1)=0
=>(m-1+4)(m-1-1)=0
=>(m+3)(m-2)=0
=>m=2(loại) hoặc m=-3
Đúng 0
Bình luận (0)



