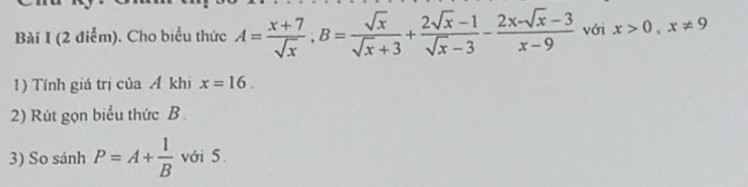giup minh cau nay voi
a. Em tự giải
b.
Phương trình hoành độ giao điểm (P) và (d):
\(-x^2=x+m-1\Leftrightarrow x^2+x+m-1=0\) (1)
(d) cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=1-4\left(m-1\right)>0\Rightarrow m< \dfrac{5}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=m-1\end{matrix}\right.\)
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{4\left(x_1+x_2\right)}{x_1x_2}+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{-4}{m-1}+m-1+3=0\)
\(\Rightarrow-4+\left(m-1\right)\left(m+2\right)=0\) (\(m\ne1\))
\(\Leftrightarrow m^2+m-6=0\Rightarrow\left[{}\begin{matrix}m=2>\dfrac{5}{4}\left(loại\right)\\m=-3\end{matrix}\right.\)
Vậy \(m=-3\)
a:
b: PTHĐGĐ là:
-x^2=x+m-1
=>-x^2-x-m+1=0
=>x^2+x+m-1=0
\(\Delta=1^2-4\left(m-1\right)=1-4m+4=5-4m\)
Để (P) cắt (d) tại hai điểm phân biệt thì 5-4m>0
=>4m<5
=>m<5/4
\(4\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
=>\(4\cdot\dfrac{x_1+x_2}{x_1x_2}+x_1x_2+3=0\)
=>\(4\cdot\dfrac{-1}{m-1}+m-1+3=0\)
=>-4+(m-1)^2+3(m-1)=0
=>(m-1+4)(m-1-1)=0
=>(m+3)(m-2)=0
=>m=2(loại) hoặc m=-3
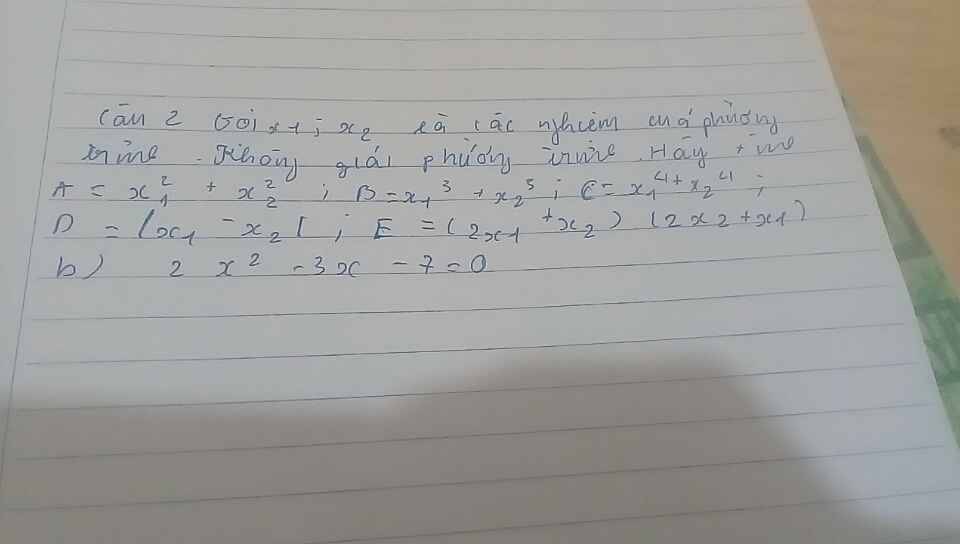
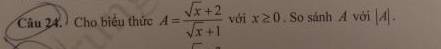
giup minh cau nay voi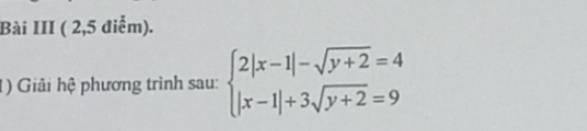
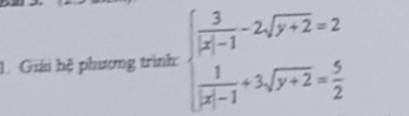giup minh cau nay voi
