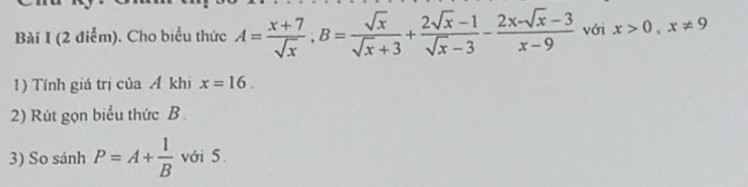a.
Phương trình hoành độ giao điểm (P) và (d):
\(\dfrac{1}{2}x^2=-\dfrac{3}{2}x+2\Leftrightarrow x^2+3x-4=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=\dfrac{1}{2}\\x=-4\Rightarrow y=8\end{matrix}\right.\)
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ là \(\left(1;\dfrac{1}{2}\right)\) và \(\left(-4;8\right)\)
b.
Phương trình hoành độ giao điểm:
\(\dfrac{1}{2}x^2=mx+2\Leftrightarrow x^2-2mx-4=0\) (1)
\(ac=-4< 0\) nên (1) luôn có 2 nghiệm trái dấu
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-4\end{matrix}\right.\)
Đặt \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4m^2+8\)
Do \(m^2\ge0;\forall m\Rightarrow2m^2+8\ge8;\forall m\)
\(\Rightarrow P_{min}=8\)
Dấu "=" xảy ra khi \(m^2=0\Rightarrow m=0\)
a: Khi m=-3/2 thì y=-3/2x+2
PTHĐGĐ là:
1/2x^2+3/2x-2=0
=>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1
=>y=1/2*(-4)^2=8 hoặc y=1/2
b: PTHĐGĐ là:
1/2x^2-mx-2=0
=>x^2-2mx-4=0
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(-4\right)=4m^2+16>0\)
=>PT luôn có hai nghiệm phân biệt
x1^2+x2^2
=(x1+x2)^2-2x1x2
=(2m)^2-2*(-4)=4m^2+8>=8
Dấu = xảy ra khi m=0



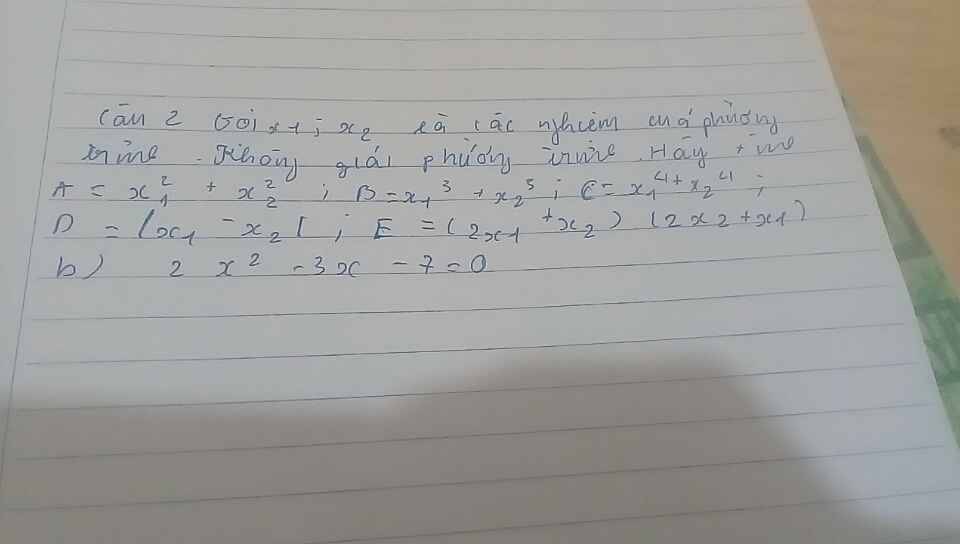

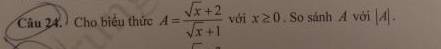
 giup minh cau nay voi
giup minh cau nay voi giup minh cau nay voi
giup minh cau nay voi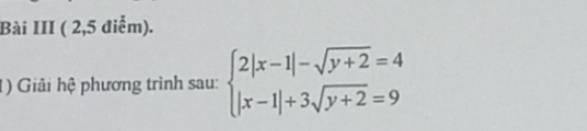
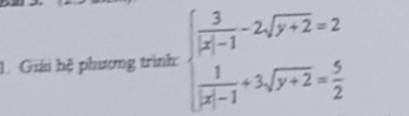 giup minh cau nay voi
giup minh cau nay voi