a, vẽ đồ thị hàm số (p) y=x² b, tìm m để đường thẳng d : y=2x + m tiếp xúc (p) Giúp e với ạ
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
LS
Những câu hỏi liên quan
a) Vẽ đồ thị hàm số y=2x² (P) b) Bằng phép tính hãy tìm giá trị của m để đường thẳng (d): y= 4x –m tiếp xúc với Parabol (P): y= 2x² Giúp mình vớiiiii
b: Phương trình hoành độ giao điểm là:
\(2x^2-4x+m=0\)
\(\text{Δ}=16-4\cdot2\cdot m=-8m+16\)
Để (P) tiếp xúc với (d) thì -8m+16=0
hay m=2
Đúng 0
Bình luận (0)
cho hàm số y=(m-2)x+3
a) Tìm m để đồ thị hàm số song song với đường thẳng y=x
b) Vẽ đồ thị với m tìm được ở câu a. Tìm tọa độ giao điểm của đồ thị vừa vẽ với đường thẳng y=2x+1
c) Tìm điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị của m
d) Tìm m để khoảng cách từ O đến đường thẳng (d) bằng 1
a/ Hai hàm số có đồ thị // với nhau khi
\(\hept{\begin{cases}m-2=1\\3\ne0\end{cases}}\Leftrightarrow m=3\)
b/ Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ
\(\hept{\begin{cases}y=x+3\\y=2x+1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=5\end{cases}}\)
c/ Gọi điểm mà đường thẳng luôn đi qua là M(a,b) ta thế vào hàm số được
\(b=ma+3\)
\(\Leftrightarrow ma+3-b=0\)
Để phương trình này không phụ thuôc m thì
\(\hept{\begin{cases}a=0\\3-b=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=0\\b=3\end{cases}}\)
Tọa độ điểm cần tìm là M(0, 3)
Đúng 0
Bình luận (0)
d/ Ta có khoản cách từ O(0,0) tới (d) là 1
\(\Rightarrow=\frac{\left|0-0m-3\right|}{\sqrt{1^2+m^2}}=\frac{3}{\sqrt{1+m^2}}=1\)
\(\Leftrightarrow\sqrt{1+m^2}=3\)
\(\Leftrightarrow m^2=8\)
\(\Leftrightarrow\orbr{\begin{cases}m=2\sqrt{2}\\m=-2\sqrt{2}\end{cases}}\)
Đúng 1
Bình luận (0)
Tìm m để đường thẳng (d): \(y=mx+4\) tiếp xúc với đồ thị hàm số (P): \(\dfrac{-x^2}{4}\) .
(hai đồ thị hàm số tiếp xúc nhau là hai đồ thị chỉ có 1 điểm chung)
Giúp mk làm bài này với
Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{4}x^2-mx-4=0\)
\(\Leftrightarrow x^2+4mx+16=0\)
\(\Delta=\left(4m\right)^2-4\cdot1\cdot16=16m^2-64\)
Để hai đồ thị tiếp xúc với nhau thì 16m2-64=0
=>m=2 hoặc m=-2
Đúng 1
Bình luận (0)
cho hàm số y=x^2 có đồ thị là P . a, vẽ P . b, tìm K để đường thẳng (d) y=2x-K+1 tiếp xúc vớ
b: Phương trình hoành độ giao điểm là:
\(x^2-2x+k-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\left(k-1\right)=-4k+4+4=-4k+8\)
Để (P) tiếp xúc với (d) thì -4k+8=0
hay k=2
Đúng 0
Bình luận (0)
Cho hàm số y=(m-1)x-4 có đồ thị đường thẳng (d)
a) tìm m để đường thẳng (d) song song với đường thẳng y=2x+5
b) vẽ đồ thị hàm số trên với m tìm được câu a
c) đường thẳng (d) cắt trục Ox tại A ,cắt trục Oy tại B .Tìm m tam giác OAB vuông góc. Mn giúp mk câu c là đc
Xem chi tiết
Cho Parabol (P) y=ax^2( a khác 0) và đường thẳng (d) y=2x-4
a. xác định a để đường thẳng (d) tiếp xúc với đường cong (P), tìm tọa độ tiếp điểm M
b. vẽ đồ thị hàm số (P) với a vừa tìm được
c. đường thẳng (d) cắt Oy tại A, tính diện tích tam giác AOM
Mọi người giúp em với ạ
Cho hai hàm số bậc nhất y=(m-1)x+2 với m khác 1 (thuộc đường thẳng d) . Y=(3-m)x-2 với m khác 3 ( thuộc đường thẳng d')
a, Tìm giá trị của M để đồ thị của hai hàm số đã cho cắt nhau
b, vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ khi m=0
Xem chi tiết
a) Để đồ thị 2 hàm số đã cho cắt nhau thì:
\(m-1\ne3-m\Leftrightarrow m\ne2\)
Vậy khi m\(\ne\)2 thì đồ thị của hai hàm số đã cho cắt nhau
b) Khi m=0 ta đc hàm số y = -x+2 và y=3x -2
* hàm số y=-x +2, cho x =0 thì y=2 => A(0;2)
, cho y=0 thì x=2 => B(2;0)
*Hàm số y =3x-2, cho x=0 thì y= -2 => C(0;-2)
cho y=0 thì x=2/3 => D(2/3; 0)
Đúng 0
Bình luận (0)
cho hàm số y=1/4x^2 có đồ thị là (p) và hàm số y=x+m có đồ thị là (d)
a) Vẽ đồ thị (p) của hàm số y=1/4x^2
b) Tìm giá trị của m để (d) tiếp xúc với (p). Tìm tọa độ tiếp điểm
a) vẽ bạn tự vẽ nha
b) Xét pt hoành độ giao điểm chung của (d) và (P) ta có:
\(\frac{1}{4}x^2=x+m\)
\(\Leftrightarrow x^2-4x-4m=0\left(1\right)\)
\(\Delta^,=4+4m\)
Để (d) tiếp xúc với (P) \(\Leftrightarrow\Delta^,=0\)
\(\Leftrightarrow4+4m=0\)
\(\Leftrightarrow m=-1\)
Thay m=-1 vào pt (1) ta được :
\(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x=2\)
\(\Rightarrow y=\frac{1}{4}.2^2=1\)
Gọi tọa độ tiếp điểm của (d) tiếp xúc với (P) là A(x,y)
=> tọa độ tiếp điểm là \(A\left(2;1\right)\)
Cho hai đường thẳng (d):y=2x-2 và (d’) :y=(m+1) x+6 (m≠-1)
a)Vẽ đồ thị hàm số (d):y=2X-2
B)Tìm m để đồ thị hai hàm số (d)và (d’) có thị song song với nhau
c)Tìm m để khoảng cách từ gốc tọa độ o đến đường thẳng (d’) bằng 3√2
a: 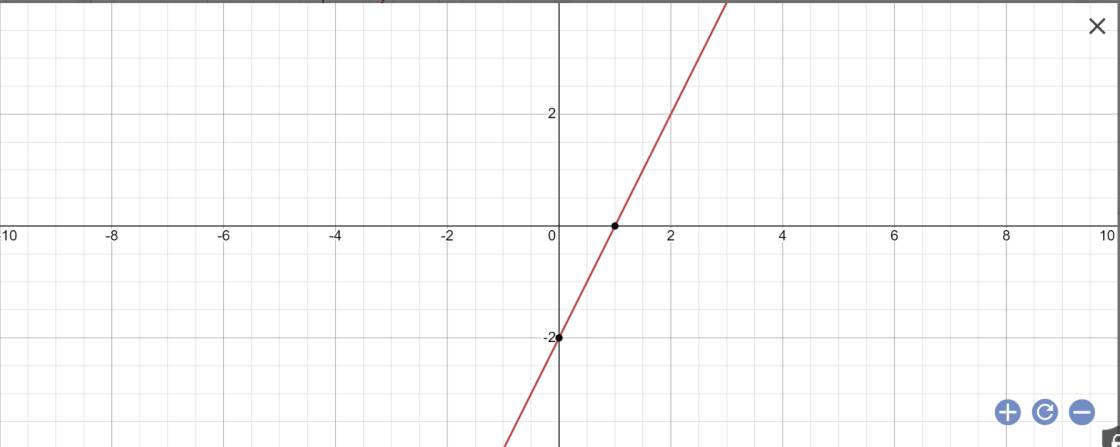
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)




