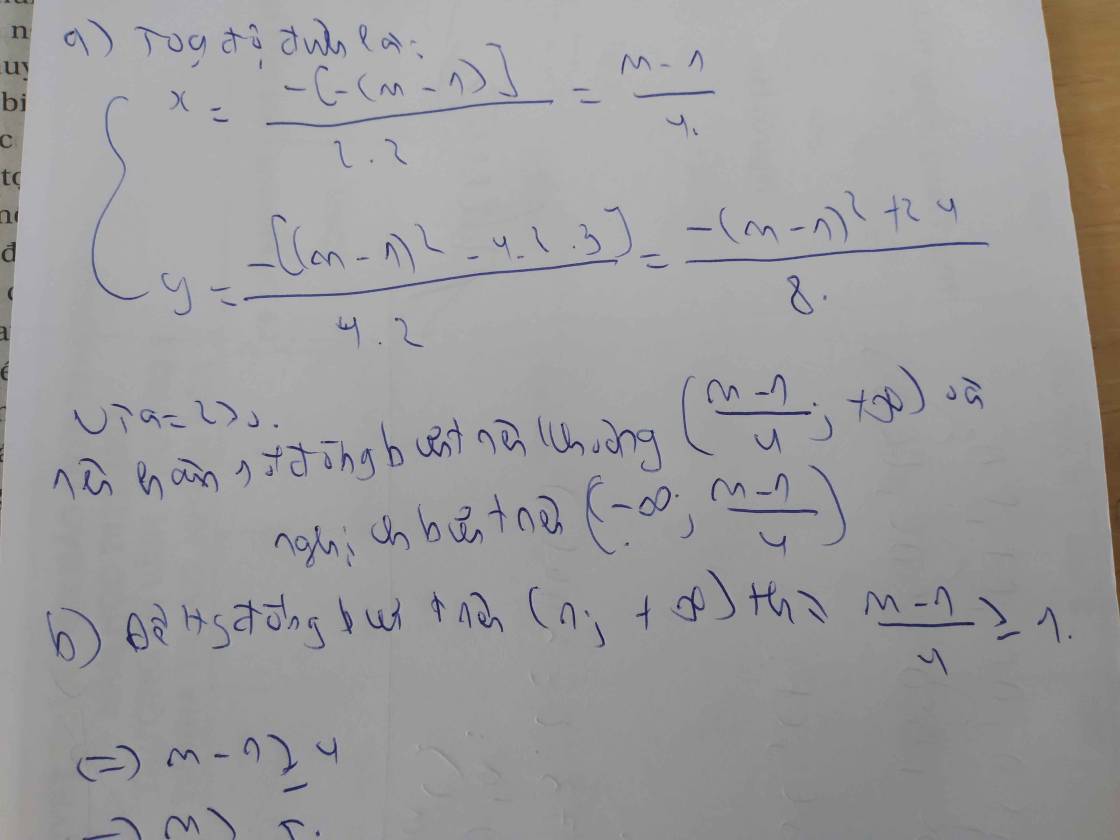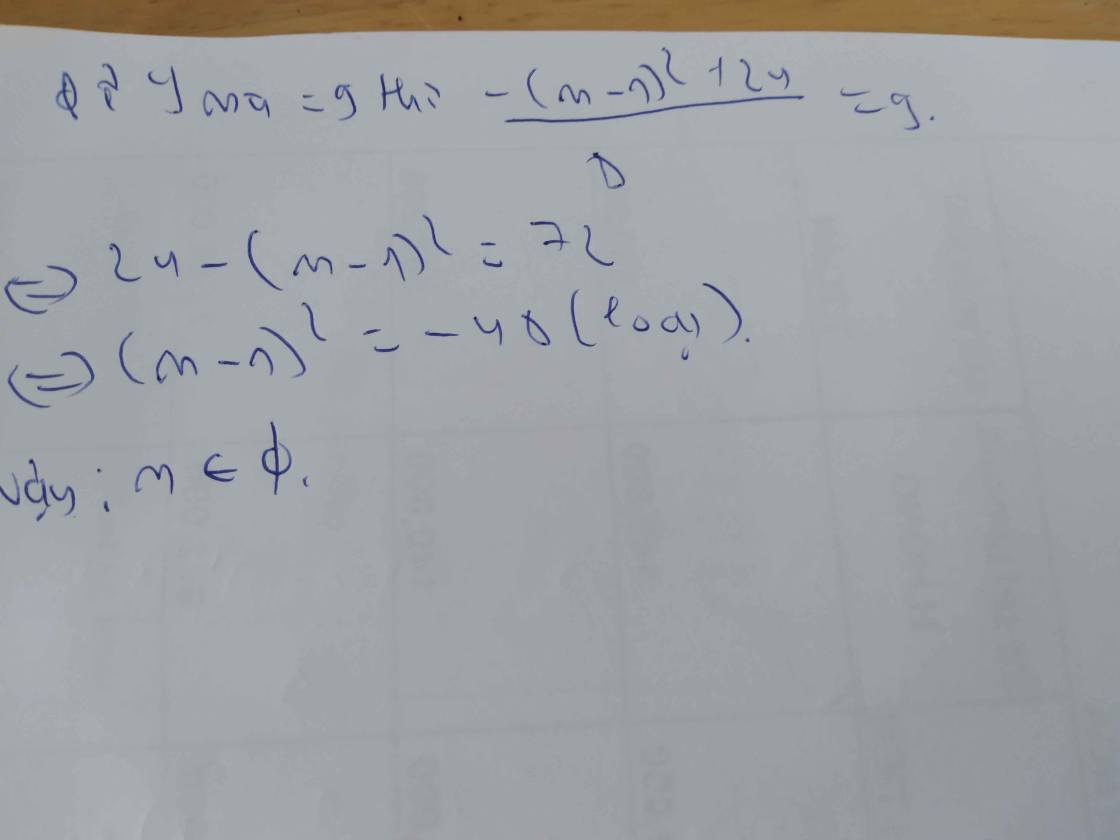Cho hàm số Y =-x2 và hàm sốY=4x2. Tìm giá trị của x để hàm số đồng biến và nghịch biến
PV
Những câu hỏi liên quan
bài 1 : Cho hàm số y=(m2-4m+3)x2
Tìm x để :
a, Hàm số đồng biến với x>0
b, hàm số nghịch biến với x>0
Bài 2 cho hàm số y=(m2-6m+12)x2
a, chứng tỏ rằng hàm số nghịch biến khi x<0 và đồng biến khi x>0
b,Khi m=2 tìm x để y=-2
c,khi m =5 tính giá trị của y biết x=1+căn 2
d, tìm m khi x=1 và y = 5
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Cho hàm số bậc nhất y=(m-2)x+ 5
a) Tìm các giá trị của m để hàm số y là hàm đồng biến
b) Tìm các giá trị của m để hàm số ý là hàm nghịch biến
a) Hàm số đồng biến trên R\(\Rightarrow a>0\Rightarrow m-2>0\Rightarrow m>2\)
b) Hàm số nghịch biến trên R
\(\Leftrightarrow a< 0\Rightarrow m-2< 0\Rightarrow m< 2\)
Đúng 0
Bình luận (0)
Tìm giá trị của M để hàm số y=5-m^2/4-m^2 nhan với x+1 để hàm số đồng biến và nghịch biến trên R
Cho hàm số bậc nhất y (m-2)x+5 với m khác 2a) Tìm các giá trịcủa m đểhàm sốy là hàm đồng biếnb) Tìm các giá trịcủa m đểhàm sốý là hàm nghịch biến.
Đọc tiếp
Cho hàm số bậc nhất y = (m-2)x+5 với m khác 2
a) Tìm các giá trịcủa m đểhàm sốy là hàm đồng biến
b) Tìm các giá trịcủa m đểhàm sốý là hàm nghịch biến.
a. \(DB:m-2>0\Leftrightarrow m>2\)
b. \(NB:m-2< 0\Leftrightarrow m< 2\)
Đúng 0
Bình luận (0)
Cho hàm số y = (m - 2)x + 3
a) Với giá trị nào của m thì hàm số đã cho là hàm số bậc nhất?
b) Trong các giá trị tìm được ở câu a, tìm những giá trị của m để hàm số đã cho đồng biến, nghịch biến ?
b: để hàm số đồng biến thì m-2>0
hay m>2
Đúng 0
Bình luận (0)
a, Để hs là hàm bậc nhất thì a\(\ne\)0
<=> m-2\(\ne0< =>m\ne2\)
b, để hs đồng biến thì a>0
<=> m-2>0<=>m>2
để hs nghichj biến thì a<0
<=> m-2<0<=>m<2
Đúng 0
Bình luận (0)
Cho hàm số y = (m2 + 2m + 5)x2. Với giá trị nào của x thì :
a) Hàm số đồng biến.
b) Hàm số nghịch biến.
c) Với x = 1 thì y = 8. Tìm m
câu a và b thay số vào là ra nhé, bài mik hơi khác:
Ta có m^2 + 2m + 3 = m^2 + 2m + 1 + 2 = (m + 1)^2 + 2 > 0 với mọi m.
Suy ra hàm số đã cho đồng biến với mọi m với x > 0 và nghịch biến với x < 0
Đúng 0
Bình luận (0)
a) Vì \(m^2+2m+5>0\forall m\) nên để hàm số \(y=\left(m^2+2m+5\right)x^2\) đồng biến thì x>0
b) Vì \(m^2+2m+5>0\forall m\) nên để hàm số \(y=\left(m^2+2m+5\right)x^2\) nghịch biến thì x<0
c) Thay x=1 và y=8 vào hàm số \(y=\left(m^2+2m+5\right)x^2\), ta được:
\(m^2+2m+5=8\)
\(\Leftrightarrow m^2+2m-3=0\)
\(\Leftrightarrow m^2+3m-m-3=0\)
\(\Leftrightarrow m\left(m+3\right)-\left(m+3\right)=0\)
\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m+3=0\\m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-3\\m=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số y=(m2+2m+3)x2 với giá trị nào của x thì:
a) Hàm số đồng biến
b) Hàm số nghịch biến
Do \(m^2+2m+3=\left(m+1\right)^2+2>0\) ; \(\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
Đúng 1
Bình luận (0)