Giúp tui dzoii=((( cảm ơn mn nhiềuu

MB
Những câu hỏi liên quan
mn giúp e với ạ e cảm ơn rất nhiềuu
Mn ơi giải giúp mình câu 6.4, 6.5 và 7.1 va ạ. Mình cảm ơn nhiềuu
6.4
\(y=\dfrac{3}{2}\left(1+cos2x\right)-\sqrt{3}sin2x+\dfrac{1}{2}-\dfrac{1}{2}cos2x\)
\(=cos2x-\sqrt{3}sin2x+2\)
\(=2\left(\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x\right)+2\)
\(=2cos\left(2x-\dfrac{\pi}{3}\right)+2\)
Do \(-1\le cos\left(2x-\dfrac{\pi}{3}\right)\le1\)
\(\Rightarrow0\le y\le4\)
\(y_{min}=0\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\)
\(y_{max}=4\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\)
Đúng 1
Bình luận (1)
6.5
Ủa nhìn bài 7 thì đây là chương trình lớp 11 (pt lượng giác) chứ đâu phải lớp 10?
Vậy giải theo kiểu lớp 11 nghe:
\(y=\dfrac{2+cosx+3sinx}{2+cosx}\)
\(\Leftrightarrow2y+y.cosx=2+cosx+3sinx\)
\(\Leftrightarrow3sinx+\left(1-y\right).cosx=2y-2\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(9+\left(1-y\right)^2\ge\left(2y-2\right)^2\)
\(\Leftrightarrow\left(y-1\right)^2\le3\)
\(\Rightarrow1-\sqrt{3}\le y\le1+\sqrt{3}\)
Đúng 1
Bình luận (0)
7.
\(\Leftrightarrow\left(m+1\right)\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-3sin^2x.cos^2x\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-\dfrac{3}{4}sin^22x\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(1-\dfrac{3}{8}\left(1-cos4x\right)\right)+cos4x=0\)
\(\Leftrightarrow\left(m+1\right)\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x=0\)
\(\Leftrightarrow5\left(m+1\right)+\left(3m+11\right)cos4x=0\)
\(\Leftrightarrow\left(3m+11\right)cos4x=-5\left(m+1\right)\)
- Với \(m=-\dfrac{11}{3}\) pt vô nghiệm
- Với \(m\ne-\dfrac{11}{3}\)
\(\Rightarrow cos4x=\dfrac{-5\left(5m+1\right)}{3m+11}\)
Do \(-1\le cos4x\le1\) nên pt có nghiệm khi:
\(-1\le\dfrac{-5\left(m+1\right)}{3m+11}\le1\)
Tới đây chắc bạn tự làm tiếp được đúng ko? Tách ra làm 2 BPT rồi sau đó giao nghiệm thôi
Đúng 1
Bình luận (1)
giúp em ạ =(( cảm ơn nhiềuu

Xem thêm câu trả lời
Giúp mình với ạ,cảm ơn nhiềuu 

giúp em với ạ em cảm ơn nhiềuu
\(\dfrac{n}{2n-1}>\dfrac{n}{2n}=\dfrac{1}{2}\)
\(\Rightarrow x_{n+1}>\dfrac{1}{2}.\left(\dfrac{x_n^2+2}{x_n}\right)\ge\dfrac{1}{2}.\dfrac{2\sqrt{2x_n^2}}{x_n}=\sqrt{2}\)
Dãy bị chặn dưới bởi \(\sqrt{2}\)
Ta sẽ chứng minh dãy đã cho là dãy giảm, hay \(x_{n+1}-x_n< 0\) với \(n>1\)
\(\Leftrightarrow\dfrac{n}{2n-1}\left(\dfrac{x_n^2+2}{x_n}\right)-x_n< 0\Leftrightarrow\left(1-n\right)x_n^2+2n< 0\)
\(\Leftrightarrow x_n^2>\dfrac{2n}{n-1}\Leftrightarrow x_n>\sqrt{\dfrac{2n}{n-1}}\)
Do \(x_n=\dfrac{n-1}{2\left(n-1\right)-1}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)=\dfrac{n-1}{2n-3}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)\ge\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}\)
Nên ta chỉ cần chứng minh: \(\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}>\sqrt{\dfrac{2n}{n-1}}\)
\(\Leftrightarrow6n-8>0\) (đúng)
Vậy dãy đã cho là dãy giảm
Dãy giảm và bị chặn dưới nên có giới hạn
Gọi giới hạn của dãy là L, lấy giới hạn 2 vế biểu thức truy hồi:
\(\lim\left(x_{n+1}\right)=\lim\left(\dfrac{n}{2n-1}.\dfrac{x_n^2+2}{x_n}\right)\Rightarrow L=\dfrac{1}{2}\left(\dfrac{L^2+2}{L}\right)\)
\(\Rightarrow L^2=2\Rightarrow L=\sqrt{2}\)
Đúng 1
Bình luận (2)
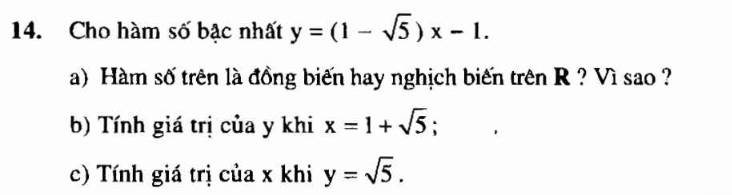 giúp e với aa, e cảm ơn nhiềuu
giúp e với aa, e cảm ơn nhiềuu
a) Hàm số trên nghịch biến trên R vì:
\(1< \sqrt{5}\Rightarrow1-\sqrt{5}< 0\)
\(\Rightarrow\) hệ số \(a< 0\)
b) Khi \(x=1+\sqrt{5}\)
\(y=\left(1-\sqrt{5}\right)\left(1+\sqrt{5}\right)-1\)
\(y=1^2-\left(\sqrt{5}\right)^2-1\)
\(y=1-5-1\)
\(y=-5\)
c) Khi \(y=\sqrt{5}\) khi và chỉ khi:
\(\left(1-\sqrt{5}\right)x-1=\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x=1+\sqrt{5}\)
\(\Leftrightarrow x=\dfrac{1+\sqrt{5}}{1-\sqrt{5}}\)
\(\Leftrightarrow x=\dfrac{\left(1+\sqrt{5}\right)^2}{1-5}\)
\(\Leftrightarrow x=-\dfrac{3+\sqrt{5}}{2}\)
Đúng 3
Bình luận (0)
Giúp em với ạ, em cảm ơn rất nhiềuu
a.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4+x}-2}{4x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{4+x}-2\right)\left(\sqrt{4+x}+2\right)}{4x\left(\sqrt{4+x}+2\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{x}{4x\left(\sqrt{4+x}+2\right)}=\lim\limits_{x\rightarrow0}\dfrac{1}{4\left(\sqrt{4+x}+2\right)}=\dfrac{1}{4\left(\sqrt{4+0}+2\right)}=\dfrac{1}{16}\)
b.
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x+7}-2\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}\)
\(=\dfrac{1}{\sqrt[3]{8^2}+2\sqrt[3]{8}+4}=\dfrac{1}{12}\)
Đúng 1
Bình luận (2)
giúp e với ạ e cảm ơn rất nhiềuu
Lời giải:
Gọi chiều dài và chiều rộng ban đầu là $a$ và $a-25$ (m)
Diện tích ban đầu: $a(a-25)$
Diện tích sau thay đổi: $(a-25)(a-25)$
Theo bài ra: $a(a-25)-(a-25)(a-25)=1000$
$\Leftrightarrow (a-25)[a-(a-25)]=1000$
$\Leftrightarrow 25(a-25)=1000$
$\Leftrightarrow a-25=40$
$\Leftrightarrow a=65$ (m)
Vậy mảnh đất ban đầu có chiều dài 65 m, chiều rộng 40 m
Đúng 0
Bình luận (0)
Mn giúp tui với tui cảm ơn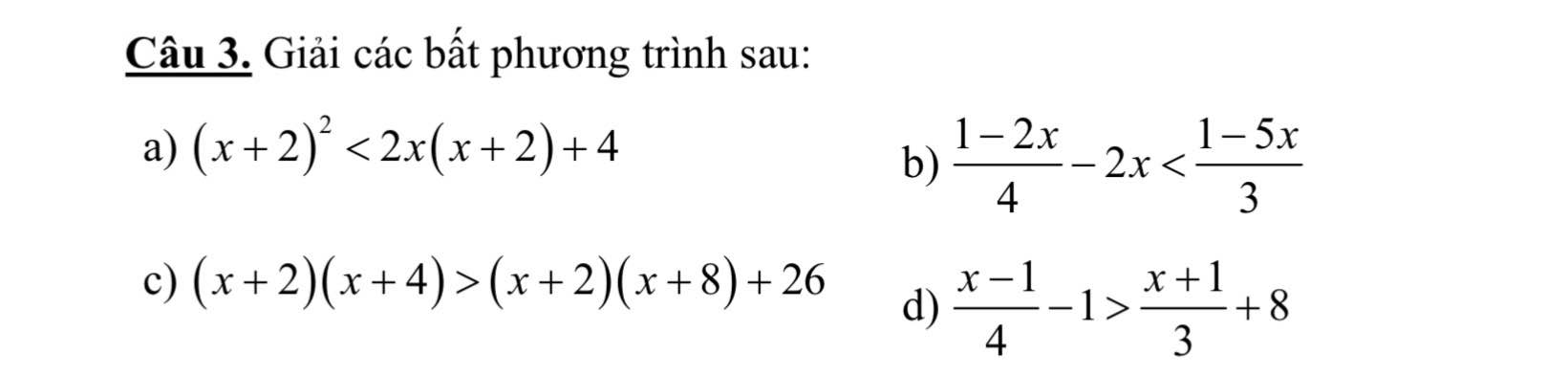
a: \(\Leftrightarrow2x\left(x+2\right)+4>x^2+4x+4\)
\(\Leftrightarrow2x^2+4x-x^2-4x>0\)
=>x<>0
b: \(\Leftrightarrow3\left(1-2x\right)-24x< 4\left(1-5x\right)\)
=>3-6x-24x<4-20x
=>-30x+3<4-20x
=>-10x<1
hay x>-1/10
c: \(\Leftrightarrow x^2+6x+8>x^2+10x+16+26\)
=>6x+8>10x+42
=>-4x>34
hay x<-17/2
Đúng 1
Bình luận (0)





