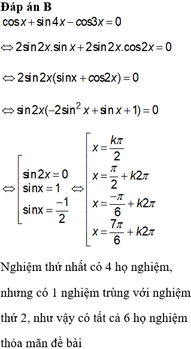2sin2x+sin4x/2(cosx+cos3x)=tan2x.cosx
NN
Những câu hỏi liên quan
Chứng minh đẳng thức:
\(\dfrac{2sin2x+sin4x}{2\left(cosx+cos3x\right)}\)=\(tan2x.cosx\)
\(VT=\dfrac{2\cdot sin2x+2\cdot sin2x\cdot cos2x}{2\cdot\left(cosx+cos3x\right)}\)
\(=\dfrac{2\cdot sin2x\left(1+cos2x\right)}{2\cdot\left(cosx+cos3x\right)}\)
\(=\dfrac{sin2x\cdot\left(1+2cos^2x-1\right)}{cosx+cos3x}\)
\(=\dfrac{sin2x\cdot2\cdot cos^2x}{2\cdot cos\left(\dfrac{3x+x}{2}\right)\cdot cos\left(\dfrac{3x-x}{2}\right)}\)
\(=\dfrac{sin2x\cdot cos^2x}{cosx\cdot cos2x}=\dfrac{sin2x}{cos2x}\cdot cosx=tan2x\cdot cosx\)
Đúng 1
Bình luận (0)
1/ Chứng minh:
a) \(\dfrac{2sin2x+sin4x}{2\left(cos3x+cosx\right)}=tan2x.cosx\)
b) \(cosx-\dfrac{1}{2}cos3x-\dfrac{1}{2}cos5x=8sin^2x.cos^3x\)
2/ Tìm m để BPT thỏa ∀x∈R
a) \(\dfrac{mx^2+2\left(m-1\right)x+4m}{3x^2-5x+8}< 0\)
b) \(\dfrac{\left(1-3m\right)x^2+2mx+1-m}{x^2+x-3}< 0\)
1. sin^8(x) - cos^8(x) - 4sin^6(x) + 6sin^4(x) - 4sin^2(x) = 1
2. sin6x+sin4x+sin2x/1+cos2x+cos4x = 2sin2x
3. 1+sin2x /cosx+sinx - 1-tan^2(x/2)/1+tan^2(x/2) = sinx
4. cos4x + 4cos2x + 3 = 8cos^4(x)
5. 1+cosx+cos2x+cos3x/ 2cos^2(x)+cosx-1 = 2cosx
1. sin^8(x) - cos^8(x) - 4sin^6(x) + 6sin^4(x) - 4sin^2(x) = 1
2. sin6x+sin4x+sin2x/1+cos2x+cos4x = 2sin2x
3. 1+sin2x /cosx+sinx - 1-tan^2(x/2)/1+tan^2(x/2) = sinx
4. cos4x + 4cos2x + 3 = 8cos^4(x)
5. 1+cosx+cos2x+cos3x/ 2cos^2(x)+cosx-1 = 2cosx
\(sin^8x-cos^8x-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-sin^2x\right)^4-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-4sin^2x+6sin^4x-4sin^6x+sin^8x\right)-4sin^6x+6sin^4x-4sin^2x\)\(=-1\) (bạn chép nhầm đề)
b/ \(\frac{sin6x+sin2x+sin4x}{1+cos2x+cos4x}=\frac{2sin4x.cos2x+sin4x}{1+cos2x+2cos^22x-1}=\frac{sin4x\left(2cos2x+1\right)}{cos2x\left(2cos2x+1\right)}=\frac{sin4x}{cos2x}=\frac{2sin2x.cos2x}{cos2x}=2sin2x\)
c/ \(\frac{1+sin2x}{cosx+sinx}-\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}=\frac{sin^2x+cos^2x+2sinx.cosx}{cosx+sinx}-\left(1-tan^2\frac{x}{2}\right)cos^2\frac{x}{2}\)
\(=\frac{\left(sinx+cosx\right)^2}{sinx+cosx}-\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)=sinx+cosx-cosx=sinx\)
d/ \(cos4x+4cos2x+3=2cos^22x-1+4cos2x+3\)
\(=2\left(cos^22x+2cos2x+1\right)=2\left(cos2x+1\right)^2=2\left(2cos^2x-1+1\right)^2=8cos^4x\)
e/
Đúng 0
Bình luận (1)
a) sin3x + cos3x = √2sin2x b) (cosx + √2sinx)(1-cosx)=sin^2x
Cho phương trình: cosx + sin4x - cos3x = 0. Phương trình trên có bao nhiêu họ nghiệm x = a + k 2 π ?
A. 2
B. 6
C. 3
D. 5
Cho phương trình: cosx + sin4x - cos3x =0. Phương trình trên có bao nhiêu họ nghiệm x = a+k2 π
A. 2
B. 6
C. 3
D. 5
Đáp án B

Nghiệm thứ nhất có 4 họ nghiệm , nhưng có 1 nghiệm trùng với nghiệm thứ 2, như vậy
có tất cả 6 họ nghiệm thỏa mãn đề bài
Đúng 0
Bình luận (0)
9. Rút gọn các biểu thức sau
A= cos7x - cos8x - cos9x + cos10x / sin7x - sin8x - sin9x + sin10x
B = sin2x + 2sin3x + sin4x / sin3x +2sin4x + sin5x
C= 1+cosx + cos2x + cos3x / cosx + 2cos^2 . x -1
D = sin4x + sin5x + sin6x / cos4x + cos5x + cos6x
\(D=\frac{sin4x+sin5x+sin6x}{cos4x+cos5x+cos6x}\)
\(=\frac{\left(sin4x+sin6x\right)+sin5x}{\left(cos4x+cos6x\right)+cos5x}\)
\(=\frac{2sin\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+sin5x}{2cos\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+cos5x}\)
\(=\frac{2sin5x.cos\left(-x\right)+sin5x}{2cos5x.cos\left(-x\right)+cos5x}=\frac{sin5x\left(2.cos\left(-x\right)+1\right)}{cos5x\left(2.cos\left(-x\right)+1\right)}=\frac{sin5x}{cos5x}=tan5x\)
Đúng 0
Bình luận (0)
Giải pt sau:
\(sin4x+1=2sinx\left(1+cosx\right)+cos3x\)
\(sin4x+1-2sinx-sin2x-cos3x=0\)
\(\Leftrightarrow2cos3x.sinx-cos3x+1-2sinx=0\)
\(\Leftrightarrow cos3x\left(2sinx-1\right)-\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(cos3x-1\right)\left(2sinx-1\right)=0\Rightarrow\left[{}\begin{matrix}cos3x=1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{k2\pi}{3}\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)