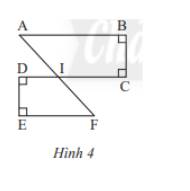
Quan sát Hình 4. Chứng minh rằng:
a) AB // CD và EF // CD
b) AB // EF
Cho hình thang ABCD, AB song song với CD có AB=7,5 cm, CD=12 cm. Gọi M là trung điểm của CD, E là giao điểm AM và BD, F là giao điểm BM và AC. Chứng minh rằng:
a, EF song song với AB
b, Tính EF
a) Ta có: AB//CD(AB và CD là hai đáy của hình thang ABCD)
nên AB//MC
Xét ΔAFB và ΔCFM có
\(\widehat{FAB}=\widehat{FCM}\)(hai góc so le trong, AB//MC)
\(\widehat{AFB}=\widehat{CFM}\)(hai góc đối đỉnh)
Do đó: ΔAFB\(\sim\)ΔCFM(g-g)
nên \(\dfrac{FA}{FC}=\dfrac{FB}{FM}=\dfrac{AB}{CM}\)
mà CM=DM(M là trung điểm của CD)
nên \(\dfrac{BF}{FM}=\dfrac{AB}{DM}\)(1)
Ta có: AB//CD(Hai cạnh đáy của hình thang ABCD)
nên AB//DM
Xét ΔABE và ΔMDE có
\(\widehat{ABE}=\widehat{MDE}\)(hai góc so le trong, AB//DM)
\(\widehat{AEB}=\widehat{MED}\)(hai góc đối đỉnh)
Do đó: ΔABE\(\sim\)ΔMDE(g-g)
nên \(\dfrac{AB}{DM}=\dfrac{AE}{EM}\)(2)
Từ (1) và (2) suy ra \(\dfrac{BF}{FM}=\dfrac{AE}{EM}\)
Xét ΔAMB có
E\(\in\)AM(Gt)
F\(\in\)BM(gt)
\(\dfrac{BF}{FM}=\dfrac{AE}{EM}\)(cmt)
Do đó: EF//AB(Định lí Ta lét đảo)
a/ Có AB // DM
=> t/g ABE đồng dạng t/g MDE (đ/l)
=> AE/ME = AB/MD = AB/MC (1)
Có AB // CM
=> t/g ABF đồng dạng t/g CMF (đ/l)
=> AF/MF = AB/CM (2)(1) ; (2)
=> AE/ME = AF/MF
Xét t/g AMB có AE/ME=AF/MF
=> EF // BC (Thales đảo)
b/ Xét t/g DEM có AB // DM
=> ME/AM = DM/AB (Hệ quả đ.l Thales)
Xét t/g AMB có EF // AB
=> ME/AM = EF/AB (Hệ quả Thales)
Do đó EF = DM = 1/2DC = 6 (cm)P/s: câu b không chắc lắm.
24
THÔNG BÁO
XEM TẤT CẢ
Hãy tham gia nhóm Học sinh Hoc24OLM
Nahida ơi bạn nhập bài muốn hỏi vào đây
Thu Anh
Thu Anh
27 tháng 1 2021 lúc 19:27
Bài 3:Cho hình thang ABCD(AB//CD) có AB = 15 cm, CD = 20 cm . Gọi M là trung điểm của CD , E là giao điểm của AM và BD . a) Chứng minh EM = 2/3 EA . b) Gọi F là giao điểm của AC và BM.Tính EF c) chứng minh AF.AM.MC = AB.AC.ME Mn giúp mk vs ạ :((
Lớp 8
Toán
NHỮNG CÂU HỎI LIÊN QUAN
Ngân Lê Bảo
Ngân Lê Bảo
30 tháng 1 2021 lúc 21:00
Cho hình thang ABCD, AB song song với CD có AB=7,5 cm, CD=12 cm. Gọi M là trung điểm của CD, E là giao điểm AM và BD, F là giao điểm BM và AC. Chứng minh rằng:
a, EF song song với AB
b, Tính EF
Xem chi tiết
Theo dõi
Báo cáo
Lớp 8
Toán
2
0
Viết câu trả lời giúp Ngân Lê Bảo
Nahida
Nguyễn Lê Phước Thịnh
Nguyễn Lê Phước Thịnh CTV
30 tháng 1 2021 lúc 21:14
a) Ta có: AB//CD(AB và CD là hai đáy của hình thang ABCD)
nên AB//MC
Xét ΔAFB và ΔCFM có
ˆ
F
A
B
=
ˆ
F
C
M
(hai góc so le trong, AB//MC)
ˆ
A
F
B
=
ˆ
C
F
M
(hai góc đối đỉnh)
Do đó: ΔAFB
∼
ΔCFM(g-g)
nên
F
A
F
C
=
F
B
F
M
=
A
B
C
M
mà CM=DM(M là trung điểm của CD)
nên
B
F
F
M
=
A
B
D
M
(1)
Ta có: AB//CD(Hai cạnh đáy của hình thang ABCD)
nên AB//DM
Xét ΔABE và ΔMDE có
ˆ
A
B
E
=
ˆ
M
D
E
(hai góc so le trong, AB//DM)
ˆ
A
E
B
=
ˆ
M
E
D
(hai góc đối đỉnh)
Do đó: ΔABE
∼
ΔMDE(g-g)
nên
A
B
D
M
=
A
E
E
M
(2)
Từ (1) và (2) suy ra
B
F
F
M
=
A
E
E
M
Xét ΔAMB có
E
∈
AM(Gt)
F
∈
BM(gt)
B
F
F
M
=
A
E
E
M
(cmt)
Do đó: EF//AB(Định lí Ta lét đ
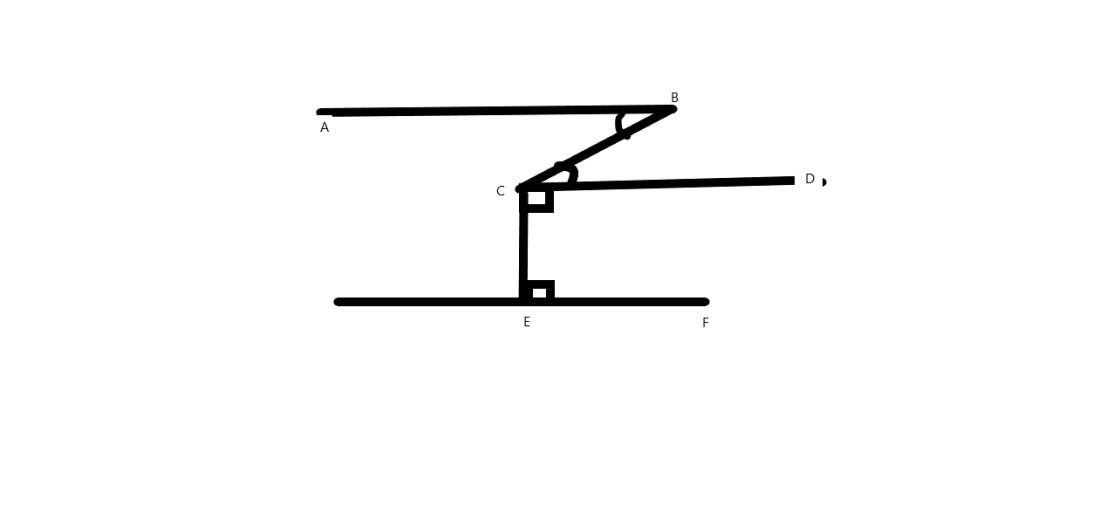
a) chứng minh AB//CD
b) chứng minh AB//EF
a) Ta có:
\(\widehat{ABC}=\widehat{BCD}\) (gt)
Nên hai góc này so le trong
⇒ AB//CD
b) Ta có:
\(\widehat{DCE}=\widehat{CEF}=90^o\) (gt)
⇒ EF//CD
Mà: AB//CD
⇒ AB//EF
có :
`góc ABC = góc BCD`
Mà 2 góc này ở vị trí solo trong
`=>AB` // `CD`
có :
\(DC\perp CE\)
\(EF\perp CE\) `=> DC` // `EF`
lại có :AB//CD
CD//EF = > AB//EF
Cho hình thang ABCD (AB//CD)AB<CD gọi E ,F lần lượt là trung điểm của AC và BD . Chứng minh EF//AB//CD và EF=(CD-AB):2
*Chứng minh EF // AB // CD
Gọi P là trung điểm AD có ngay:PF // AB (2) (PF là đường trung bình tam giác DAB)
Lại có PE // DC(là đường trung bình tam giác ADC) và DC // AB nên PE // AB(2)
Từ (1) và (2) theo tiên đề Ơclit suy ra P, E, F thẳng hàng. Mà PF // AB -> FE // AB(3)
Lại có PE // DC -> FE // DC (4). Từ (3) và (4) suy ra đpcm.
* Chứng minh EF = \(\frac{CD-AB}{2}=\frac{CD}{2}-\frac{AB}{2}\).
Do PE = 1/2 CD; PF = 1/2 AB và P, E, F thẳng hàng nên:
\(PF+FE=PE\Leftrightarrow\frac{1}{2}AB+FE=\frac{1}{2}CD\Leftrightarrow FE=\frac{CD-AB}{2}\)
=> đpcm
P/s: ko chắc.
Giúp mik gấp vs ạ
Đề: Cho hình thang ABCD(AB//CD) có AB< hoặc bằng CD. Gọi E và F lần lượt là trung điểm của DB và AC. Chứng minh EF//AB//CD và EF= (CD-AB):2
cho hình thang ABCD ( AB //CD ) . gọi E , F lần lượt là trung điểm của BD và AC .
a, chứng minh EF// CD
b, chứng minh EF = ( CD - AB ) : 2
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC.
Chứng minh rằng:
a) EI//CD, IF//AB.
b)EF=<AB+CD/2
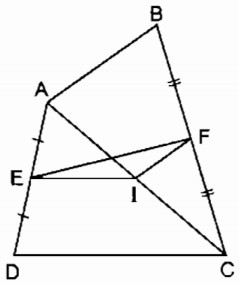
a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Và EI=CD/2
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
Và IF=AB/2
b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)
Mà EI=\(\dfrac{CD}{2}\); IF=\(\dfrac{AB}{2}\) (chứng minh trên) ⇒EF≤\(\dfrac{CD}{2}+\dfrac{AB}{2}\)
Vậy EF≤\(\dfrac{AB+CD}{2}\) (dấu bằng xảy ra khi AB // CD)
Tick nha 😘
a) Xét ΔACD có
I là trung điểm của AC
E là trung điểm của AD
Do đó: EI là đường trung bình của ΔACD
Suy ra: EI//CD
Xét ΔABC có
I là trung điểm của AC
F là trung điểm của BC
Do đó: IF là đường trung bình của ΔABC
Suy ra: IF//AB
Cho hình bình hành ABCD. Trên các cạnh AB, CD lần lượt lấy E,F sao cho AE=CF. Chứng minh rằng:
a) Tứ giác AECF là hình bình hành
b) BF//ED
c) Các đường thẳng AC; EF; BD đồng quy.
Bài 4.Cho hình thang ABCD (AB // CD). Gọi M là trung điểm
của CD, E là giao điểm của MA và BD, F là giao điểm của MB
và AC.
a) Chứng minh EF // AB
b) Tính EF biết AB = 7,5cm, CD = 12cm
Cho tứ giác ABCD. Gọi E, F, I là trung điểm của AD, BC, AC. Chứng minh rằng:
a) EI // CD; IF // AB.
b) EF ≤ (AB+CD)/2
3*đừng để ý
a: Xét ΔACD có
E là trung điểm của AD
I là trung điểm của AC
Do đó: EI là đường trung bình của ΔACD
Suy ra: EI//CD
Xét ΔACB có
F là trung điểm của BC
I là trung điểm của AC
Do đó: FI là đường trung bình của ΔACB
Suy ra: FI//AB
Bài 1: Cho tứ giác ABCD. Gọi E, F, I là trung điểm của AD, BC, AC. Chứng minh rằng:
a) EI // CD; IF // AB.
b) EF ≤ (AB+CD)/2
Bài 4: Cho tam giác ABC có đường truyến BD và CE cắt nhau tại G. Gọi I, K là trung điểm GB, GC. Chứng minh DE// IK và DE = IK.
Bài 5: Cho tam giác ABC có đường trung tuyến BD và CE. Gọi M, N là trung điểm BE, CD. Gọi MN cắt BD tại I và MN cắt CE tại I. Chứng minh MI = IK = KN