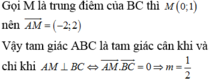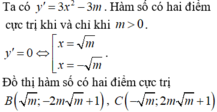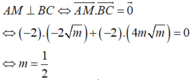Cho A (11,4), B(8,2), C(13,y). Tìm y để tam giác ABC cân tại A
XO
Những câu hỏi liên quan
Cho y = x3-3mx+1 có điểm A (2;3). Tìm m để hàm số có hai cực trị B,C sao cho tam giác ABC cân tại A
ta co y'=3x2-3m. h/s co 2 diem cuc tri<=>y'=0 co 2no pbiet # 2 <=>Δ>0 g(2)#0 <=>-4.3.(-3m)>0 3.(-2)2-3m#0 <=>m>0 m#4 ' ▲y'=0 =>x1=can(m) hoac x2=-can(m) (*) goi B(x1,x13-3mx1+1) va C(x2,x23-3mx2+1) thay (*) vao toa do B,C tinh vecto AB va vecto AC Cho 2 vecto dok =nhau binh phuong 2 ve => giai ra m. ket hop voi dk phia tren roi ket luan
Đúng 0
Bình luận (0)
Cho hàm số y=x3-3mx+1 (1). Cho A(2;3) tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A
A. m=-1/2
B. m=-3/2
C. m=1/2
D. m=3/2
Cho hàm số
y
x
3
-
3
m
x
+
1
(1). Cho A(2;3) , tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A.
Đọc tiếp
Cho hàm số y = x 3 - 3 m x + 1 (1). Cho A(2;3) , tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A.
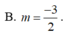
![]()
![]()
cho tam giác abc vuông taị a tổng cạnh ab và aclà17,7cm .nếu tăng cạnh ac lên 11,4 cm và giữ nguyên cạnh ab thì ta tam giác abc vuông cân tại a. tính diện tích abc
Cho A(2;2) d1: x+y-2=0 và d2: x+y-8=0. Gọi B và C là các điểm lần lược thuộc d1, d2 sao cho tam giác ABC vuông cân tại A, tìm B,C
\(d1:x+y-2=0\Leftrightarrow y=-x+2\Rightarrow B\left(a;-b+2\right)\)
\(d2:x+y-8=0\Leftrightarrow y=-x+8\Rightarrow C\left(b;-b+8\right)\)
\(\Rightarrow AB=\sqrt{\left(a-2\right)^2+\left(-a+2-2\right)^2}\)
\(\Rightarrow AC=\sqrt{\left(b-2\right)^2+\left(-b+8-2\right)^2}\)
\(\Delta ABC\) \(vuông\) \(cân\) \(tạiA\Rightarrow\left\{{}\begin{matrix}AB^2=AC^2\\\overrightarrow{AB}.\overrightarrow{AC}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(-a\right)^2=\left(b-2\right)^2+\left(-b+8-2\right)^2\\\left(a-2\right)\left(b-2\right)+\left(-a\right)\left(-b+6\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\\\left\{{}\begin{matrix}a=3\\b=5\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}B\left(-1;3\right)\\C\left(3;5\right)\end{matrix}\right.\\\left\{{}\begin{matrix}B\left(3;-1\right)\\C\left(5;3\right)\end{matrix}\right.\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông taị A tổng cạnh AB và AC là17,7cm .nếu tăng cạnh AC lên 11,4 cm và giữ nguyên cạnh AB thì ta tam giác ABC vuông cân tại A. tính diện tích ABC
Đặt AB=a,AC=b
Ta có a+b=17,7
Và a+11,4 =b
Từ đó => a+a+11,4 =17,7
=> a = 3,15
=> b= 3,15+11,4= 14,55
Cho A(-1;2) B(3;1) và đường thẳng Δ : x-y+1 = 0. Tìm C trên Δ sao cho tam giác ABC thỏa mãn:
a) tg ABC cân tại B
b)tg ABC vuông ở C
Tam giác ABC cân tại A biết A(-1;4) và B,C thuộc \(\Delta=x-y-4=0\). Tìm tọa độ B,C biết \(S_{\Delta ABC}=18\)
Cho hàm số y = ( m -1).x + 2m – 1 ( m khác 1) có đồ thị là đường thẳng (d)
a) Tìm m để (d) đi qua E ( 3, 8)
b) Tìm m để (d) cắt Ox tại A và Oy tại B sao cho diện tích tam giác ABC vuông cân .
c) Tìm m để khoảng cách từ O đến (d) lớn nhất và nhỏ nhất
a: Thay x=3 và y=8 vào (d), ta được:
3(m-1)+2m-1=8
=>5m-4=8
=>5m=12
=>m=12/5
b: Tọa độ A là:
y=0 và x=(-2m+1)/(m-1)
=>OA=|2m-1/m-1|
Tọa độ B là:\
x=0 và y=2m-1
=>OB=|2m-1|
Để ΔOAB vuông cân tại O thì OA=OB
=>|2m-1|(1/|m-1|-1)=0
=>m=1/2 hoặc m=2 hoặc m=0
Đúng 0
Bình luận (0)
cho đường tròn (C) : x^2+y^2-2x=9 và điểm A( 0;1). tìm tọa độ 2 điểm B,C thuộc đường tròn sao cho tam giác ABC vuông cân tại A
Đường tròn (C) tâm \(I\left(1;0\right)\) bán kính \(R=\sqrt{10}\)
Do tam giác ABC vuông cân tại A \(\Rightarrow AB=AC\)
Lại có \(IB=IC=R\)
\(\Rightarrow AI\) là trung trực BC \(\Rightarrow AI\) đồng thời là phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{IAB}=45^0\)
\(\overrightarrow{AI}=\left(1;-1\right)\), do B thuộc đường tròn, gọi tọa độ B có dạng: \(B\left(x;y\right)\) với \(x^2+y^2-2x-9=0\)
\(\Rightarrow\overrightarrow{AB}=\left(x;y-1\right)\)
\(cos\widehat{IAB}=\dfrac{\sqrt{2}}{2}=\dfrac{\left|1.x-1\left(y-1\right)\right|}{\sqrt{2}.\sqrt{x^2+\left(y-1\right)^2}}\)
\(\Rightarrow\sqrt{x^2+y^2-2y+1}=\left|x-y+1\right|\)
\(\Rightarrow x^2+y^2-2y+1=x^2+y^2+1-2xy+2x-2y\)
\(\Rightarrow x-xy=0\Rightarrow x\left(1-y\right)=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y^2=9\Rightarrow y=\pm3\\y=1\Rightarrow x^2-2x-8=0\Rightarrow x=\left\{4;-2\right\}\end{matrix}\right.\)
Vậy tọa đô các điểm B;C tương ứng là: \(\left[{}\begin{matrix}\left(0;3\right);\left(-2;1\right)\\\left(0;-3\right);\left(4;1\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)