Cho ΔABC có diện tích là 25cm2, độ dài cạnh AB=5cm, BC=9cm. Tìm sinB
CA
Những câu hỏi liên quan
Cho ΔABC vuông tại A. Đường cao AH chia cạnh huyền thành hai đoạn có độ dài 9cm và 16cm. Diện tích tam giác vuông đó là: A. 72
c
m
2
B. 144
c
m
2
C. 150
c
m
2
D. 210
c
m
2
Đọc tiếp
Cho ΔABC vuông tại A. Đường cao AH chia cạnh huyền thành hai đoạn có độ dài 9cm và 16cm. Diện tích tam giác vuông đó là:
A. 72 c m 2
B. 144 c m 2
C. 150 c m 2
D. 210 c m 2
ΔABC có độ dài các cạnh là 3cm, 4cm, 5cm. ΔA'B'C' đồng dạng ΔABC và có diện tích là 54cm2. tính các cạnh của ΔA'B'C'.
Lời giải:
Giả sử $AB=3, AC=4, BC=5$ (cm)
Vì $3^2+4^2=5^2$ nên theo định lý Pitago đảo thì $ABC$ là tam giác vuông tại $A$
$A'B'C'$ đồng dạng với $ABC$ nên $A'B'C'$ là tam giác vuông tại $A'$
$\Rightarrow S_{A'B'C'}=\frac{A'B'.A'C'}{2}=54\Rightarrow A'B'.A'C'=108(*)$ (cm)
$ABC\sim A'B'C'\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$
$\Leftrightarrow \frac{A'B'}{3}=\frac{B'C'}{5}=\frac{C'A'}{4}(**)$
Từ $(*); (**)$ suy ra $A'B'=9; B'C'=15; C'A'=12$ (cm)
Đúng 3
Bình luận (0)
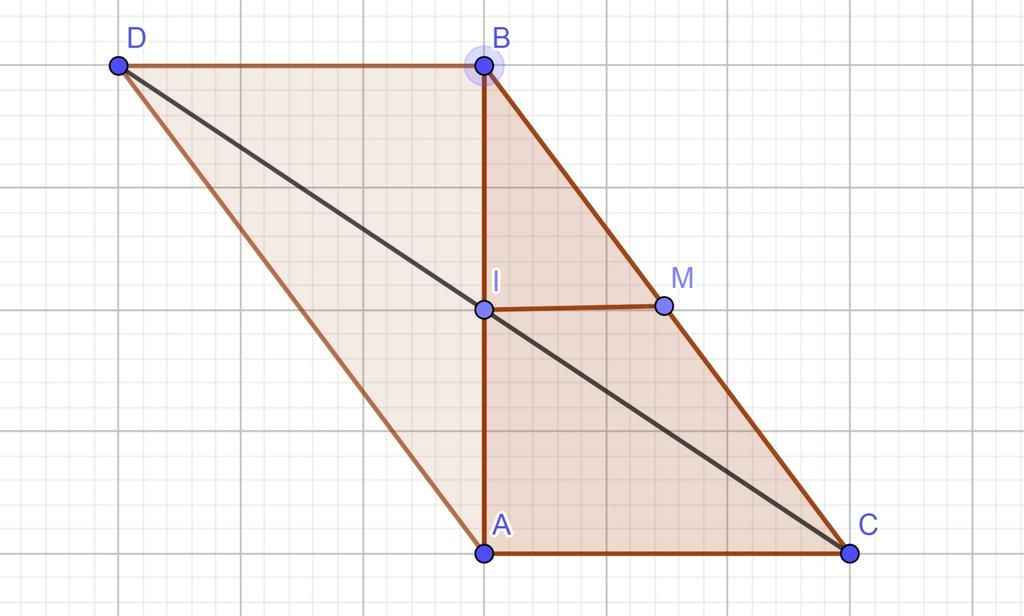
Cho tam giác ABC có A= 90 độ, AC = 5cm, BC = 13cm. Gọi I là trung điểm của cạnh AB, D là điểm đối xứng với C qua I.
a) Tứ giác ADBC là hình gì? Vì sao?
b) Gọi M là trung điểm của cạnh BC. Chứng minh: MI vuông góc với AB. Tính diện tích ΔABC.
a) Xét tứ giác \(ADBC\) ta có :
\(IB=IA\left(g.t\right)\)
\(IC=IC\) ( \(D\) đối xứng qua \(I\))
Vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Vậy tứ giác \(ADBC\) là hình bình hành
b) Xét \(\Delta ABC\) ta có :
\(IA=IB\left(g.t\right)\)
\(MB=MC\left(g.t\right)\)
\(\Rightarrow IM\) là đường trung bình \(\Delta ABC\)
Do đó : \(IM\text{/ / }AC\)
Mà \(AB\text{⊥}AC\left(A=90^o\right)\)
Vậy \(IM\text{⊥}AB\)
Áp dụng định lí pytago \(\Delta ABC\) ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)
\(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.13.5=30\left(cm^2\right)\)
Đúng 1
Bình luận (1)
1.
a) Cho ΔABC có : AC=5cm, BC=3cm. Tìm cạnh AB biết, AB là số nguyên và AB>6cm
b) Cho ΔABC có: AB=8cm, AC=6cm. Tính BC, biết BC là số nguyên BC<4cm
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A , AB =9cm ; AC =12cm.Kẻ đường cao AH
a)Chứng minh :ΔABC~ΔHBA
b)Tính độ dài : BC,AH
c) phân giác của góc ACB cắt AH tại E cắt AB tại D tính tỉ số diện tích của 2 tam giác ACD và HCE
a, Xét tam giác ABC và tam giác HBA ta có
^B _ chung
^BAC = ^BHA = 900
Vậy tam giác ABC ~ tam giác HBA (g.g)
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=15cm\)
\(\dfrac{AC}{AH}=\dfrac{BC}{AB}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{36}{5}cm\)
\(\dfrac{AB}{HB}=\dfrac{BC}{AB}\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{27}{5}cm\)
=> CH = 48/5 cm
c, \(\dfrac{S_{ACD}}{S_{HCE}}=\left(\dfrac{AC}{HC}\right)^2=\dfrac{25}{16}\)
Đúng 1
Bình luận (0)
cho tam giác ABC có AB= 6cm, AC= 5cm, BC=9cm. Điểm D thuộc cạnh BC sao cho BD= 4cm. Tính độ dài AD
Xét ΔBDA và ΔBAC có
\(\dfrac{BD}{BA}=\dfrac{BA}{BC}\)
\(\widehat{B}\) chung
Do đó: ΔBDA~ΔBAC
=>\(\dfrac{AD}{AC}=\dfrac{BD}{BA}\)
=>\(\dfrac{AD}{5}=\dfrac{4}{6}=\dfrac{2}{3}\)
=>\(AD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho hình thang vuông MNPQ vuông góc tại M và Q , kéo dài về phia N thêm 5cm thì được hình chữ nhật và có diện tích tăng thêm là 25cm2. Trung bình độ dài 2 đáy là 60cm. Hãy tìm diện tích hình thang ban đầu ?
Cho AB = 5cm, tổng độ dài hai cạnh AB và BC là 8cm. Tính diện tích hình chữ nhật.
cạnh BC là : 8 - 5 = 3 ( cm )
Diện tích hình chữ nhật là : 8 x 3 = 24 ( cm2 )
Đáp số : 24 cm2
a) Cho tam giác ABC.D là trung điểm của cạnh AB, E là trung điểm của cạnh AC.Tính độ dài cạnh BC, biết DE= 5cm
b) Một hình thang có độ dài hai đáy là 21cm và 9cm. Tính độ dài đường trung bình của hình thang đó.
Cho tam giác ABC có diện tích là 150cm2. Biết nếu kéo dài cạnh đáy BC thêm 5cm thì diện tích tăng thêm 37,5cm2. Tính độ dài cạnh đáy BC.
Chiều cao tam giác ban đầu là: 37,5 x 2 : 5 = 15(cm)
Độ dài cạnh BC là: 150 x 2 : 15 = 20 (cm)
Đáp số: 20 (cm)
Đúng 0
Bình luận (0)
Chiều cao tam giác ABC là:
37,5 x 2 : 5 = 15 (cm)
Độ dài đáy BC là:
150 x 2 : 15 = 20 (cm)
Đáp số: 20cm
Đúng 1
Bình luận (0)




