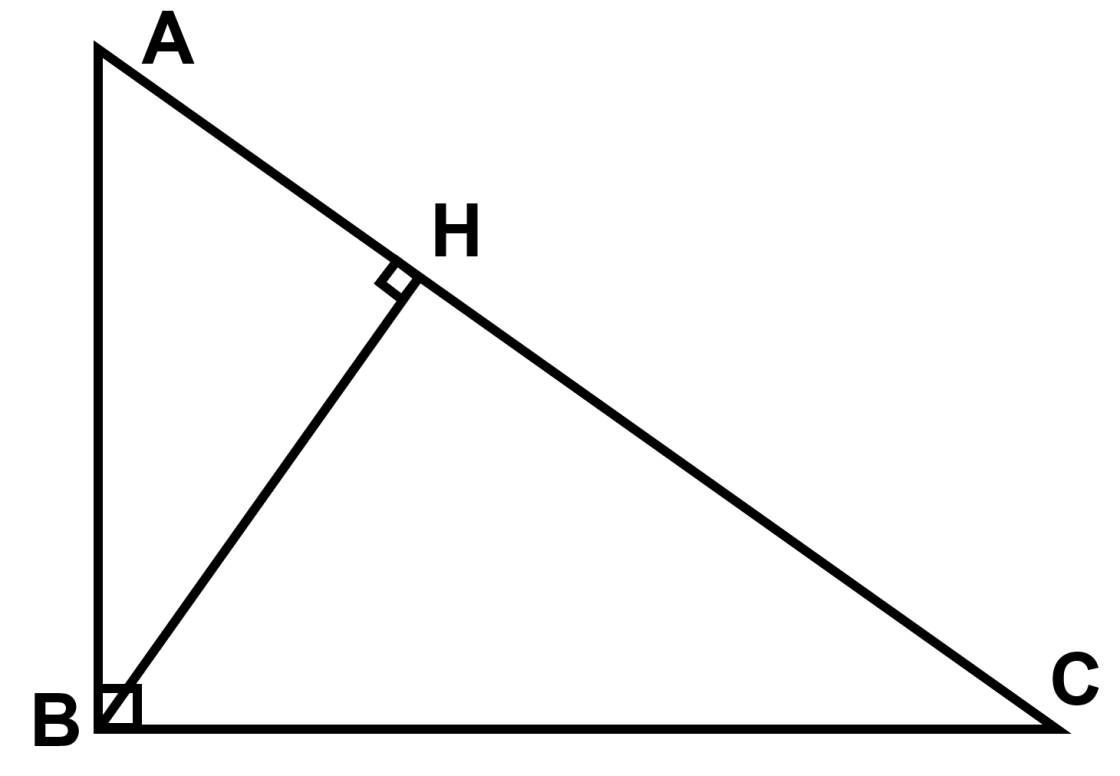
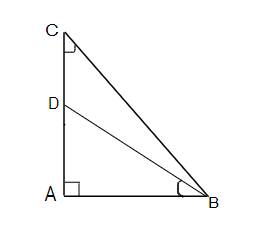
Cho tam giác ABC vuông tại A có AB = 6cm ; AC= 8cm . Đường cao AH và phân giác BD cắt nhau tại I ( H trên BC và D trên AC ) .
a) Tính độ dài AD , DC
b) Cm : tam giác ABC đồng dạng với tam giác HBA và AB^2 = BH.BC
c) Cm : tam giác ABI đồng dạng với tam giác CBD
d) Cm : \(\dfrac{IH}{IA}=\dfrac{AD}{DC}\)
( Giải giúp mình câu c với d ạ cảm ơn ^^ )