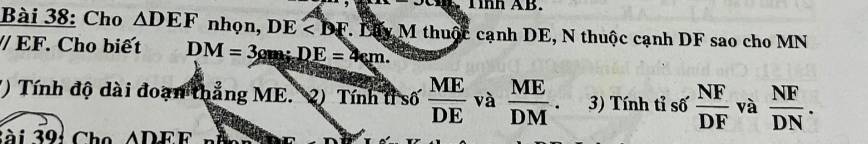Giúp mình bài hình 6
6:
a: Xét ΔAKE và ΔABC có
AK/AB=AE/AC
góc A chung
=>ΔAKE đồng dạng với ΔABC
b: ΔAKE đồng dạng vơi ΔABC
=>KE/BC=AK/AB
=>7/BC=6/9=2/3
=>BC=7:2/3=21/2(cm)
c: ΔAKE đồng dạng với ΔABC
=>góc AKE=góc ABC
=>góc EKC+góc B=180 độ
=>BEKC nội tiếp
=>góc BEC=góc BKC
Câu 18: (2,5đ) Cho hình chữ nhật ABCD ( AB < BC). Kẻ đường cao AH của ∆ABC. Kéo dài AH cắt BC tại E và cắt CD tại F.
a/ Chứng tỏ rằng ∆HBA ∆BAE và AB2 = AH. AE. b/ Chứng minh: ∆HBE ∆HAB từ đó suy ra hệ thức HB2 = HA. HE.
C/ Chứng minh rằng: AH2 = HE. HF.
a: Xét ΔHAB vuông tại H và ΔBAE vuông tại B có
góc HAB chung
=>ΔHAB đồng dạng với ΔBAE
=>AH/AB=AB/AE
=>AB^2=AH*AE
b: Xet ΔHBE vuông tại H và ΔHAB vuông tại H có
góc HBE=góc HAB
Do đo: ΔHBE đồng dạngvới ΔHAB
=>HB/HA=HE/HB
=>HB^2=HE*HA
cho góc xOy( góc xOy≠180 độ).Trên tia Ox lấy hai điểm A và B sao cho OA=4cm,OB=12cm>trên tia Oy lấy hai điểm C và D sao cho OC=6cm,OD=8cm
a,c/m 2 tam giác OCB và OAD đồng dạng
b,Gọi giao điểm của các cạnh AD và BC là I,chứng minh rằng hai tam giác AIB và ICD có các góc bằng nhau từng đôi một
a: Xet ΔOCB và ΔOAD có
OC/OA=OB/OD
góc O chung
=>ΔOCB đồng dạng với ΔOAD
b: ΔOCB đồng dạng với ΔOAD
=>góc OCB=góc OAD
=>góc IAB=góc ICD
=>góc IBA=góc IDC; góc AIB=góc CID
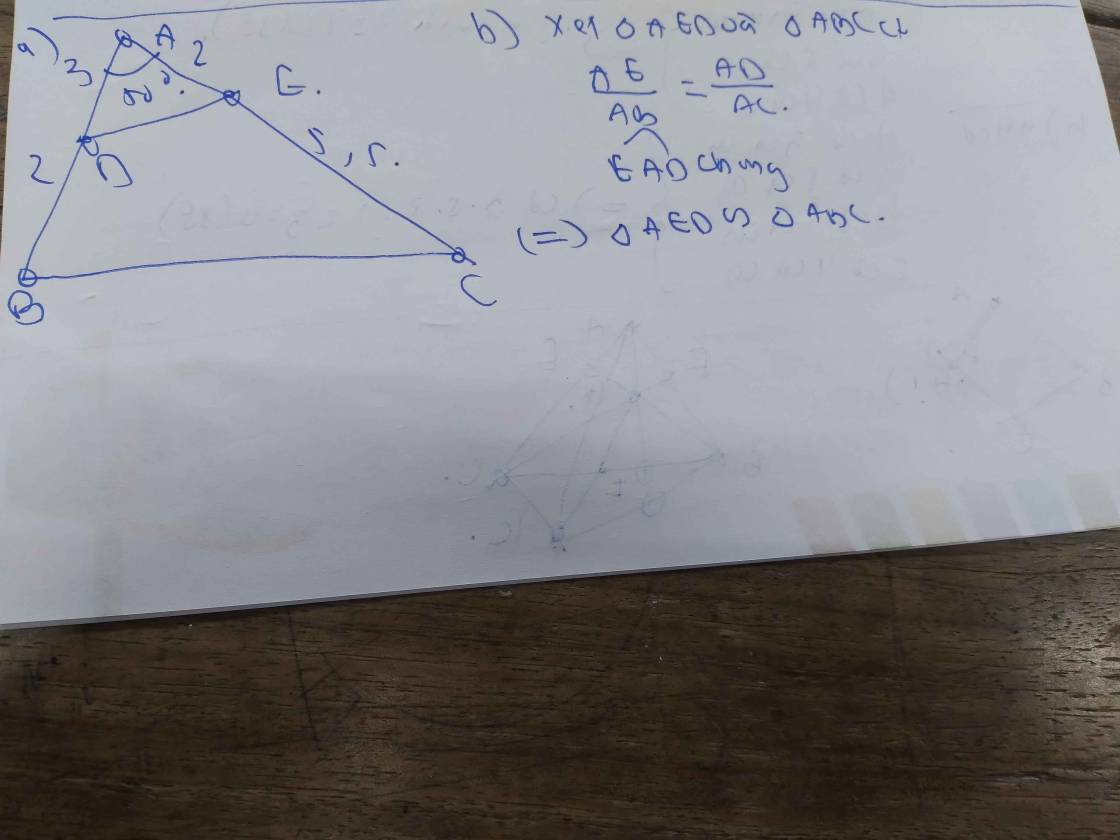
a, vẽ tam giác ABC có góc BAC=50 độ ,AB=5cm;AC=7,5 cm
b,lấy trên các cạnh AB,AC lần lượt hai điểm D,E sao cho AD=3cm;AE=2cm.Hai tam giác AED và ABC có đồng dạng với nhau k?Vì sao?
b: Xet ΔAED và ΔABC có
AE/AB=AD/AC
góc A chung
=>ΔAED đồng dạng với ΔABC
cho góc xOy( góc xOy≠180 độ).Trên tia Ox lấy hai điểm A và B sao cho OA=4cm,OB=12cm>trên tia Oy lấy hai điểm C và D sao cho OC=6cm,OD=8cm
a,c/m 2 tam giác OCB và OAD đồng dạng
b,Gọi giao điểm của các cạnh AD và BC là I,chứng minh rằng hai tam giác AIB và ICD có các góc bằng nhau từng đôi một
a: Xet ΔOCB và ΔOAD có
OC/OA=OB/OD
góc O chung
=>ΔOCB đồng dạng với ΔOAD
b: ΔOCB đồng dạng với ΔOAD
=>góc OCB=góc OAD
=>góc IAB=góc ICD
=>góc IBA=góc IDC; góc AIB=góc CID
1
a, vẽ tam giác ABC có góc BAC=50 độ ,AB=5cm;AC=7,5 cm
b,lấy trên các cạnh AB,AC lần lượt hai điểm D,E sao cho AD=3cm;AE=2cm.Hai tam giác AED và ABC có đồng dạng với nhau k?Vì sao?
Bài 7. Cho tam giác ABC vuông ở A, đường cao AH.
a. Chứng minh AABC ~ HAC
b. Chứng minh AH2 = HB. HC
c. Cho AC = 10cm, CH = 8cm. Tính độ dài AH và diện tích tam giác ABC
d. Gọi P và Q lần lượt là trung điểm của AH và CH. Gọi M là giao điểm của AQ và BP.
Chứng minh AQ L BP và AH2 = 4PM. PB
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng vơi ΔHAC
b: Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
c: \(AH=\sqrt{10^2-8^2}=6\left(cm\right)\)
HB=6^2/8=4,5cm
BC=8+4,5=12,5cm
S=6*12,5/2=37,5cm2
Cho tam giác ABC nhọn có AB= 2 cm; AC= 3,5 cm. Trên tia AB và AC lần lượt lấy M và N sao cho AM= 7 cm, AN = 4 cm
a) C/m tam giác ABC đồng dạng với tam giác ANM
b) Cho BC = 4,5 cm. Tính độ dài đoạn thẳng MN
a: Xét ΔABC và ΔANM có
AB/AN=AC/AM
góc A chung
=>ΔABC đồng dạng với ΔANM
b: ΔABC đồng dạng với ΔANM
=>BC/NM=AB/AN
=>4,5/NM=2/4=1/2
=>NM=9cm
1: ME=4-3=1cm
2: ME/DE=1/4
ME/DM=3
