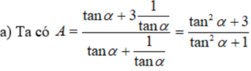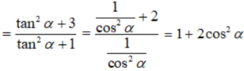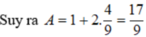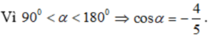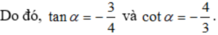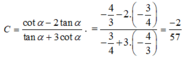Cho sinα+cosα = \(\dfrac{3}{5}\)
Tính giá trị của: C = sin(180-α) . cos (180-α).
Em cảm ơn ạ.
BP
Những câu hỏi liên quan
~Các bạn giúp mk làm bài này nhé! Cảm ơn các bạn nhiều ...~ Bài 1:Tính giá trị biểu thứca) A sin10°+sin20°+sin30°+sin40°-cos50°-cos60°-cos70°-cos80°b) C cos²52° sin45°+sin²52° cos45°c) E sin²5°+sin²15°+sinv25°+sin²35°+sin²45°+sin²55°+sin²65°+sin²75°+sin²85°Bài 2: C/m rằng với góc nhọn α ta luôn cóa) (sinα +cosα)²-(sinα -cosα)² 4sinα cosαb) cosα/1-sinα 1+sinα/cosαc) √̅s̅i̅n̅²̅x̅(̅1̅+̅̅c̅o̅t̅̅x̅)̅̅+̅c̅o̅s̅²̅x̅(̅1̅+̅t̅a̅n̅x̅)̅ sinx+cosxBài 3: Cho α là một góc nhọn a) Biết sinα 3/4. Tính cosα(90°-...
Đọc tiếp
~Các bạn giúp mk làm bài này nhé! Cảm ơn các bạn nhiều ...~
Bài 1:Tính giá trị biểu thức
a) A= sin10°+sin20°+sin30°+sin40°-cos50°-cos60°-cos70°-cos80°
b) C= cos²52° sin45°+sin²52° cos45°
c) E= sin²5°+sin²15°+sinv25°+sin²35°+sin²45°+sin²55°+sin²65°+sin²75°+sin²85°
Bài 2: C/m rằng với góc nhọn α ta luôn có
a) (sinα +cosα)²-(sinα -cosα)² = 4sinα cosα
b) cosα/1-sinα =1+sinα/cosα
c) √̅s̅i̅n̅²̅x̅(̅1̅+̅̅c̅o̅t̅̅x̅)̅̅+̅c̅o̅s̅²̅x̅(̅1̅+̅t̅a̅n̅x̅)̅ =sinx+cosx
Bài 3: Cho α là một góc nhọn
a) Biết sinα =3/4. Tính cosα(90°-α)
b) Biết tanα =2. Tính cotα(90°-α)
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Đúng 0
Bình luận (0)
a) Cho
cos
α
2
3
. Tính giá trị của biểu thức
A
tan
α
+
3
c
o
t
α
tan
α
+
c
o
t
α
b) Cho
sin
α
3
5...
Đọc tiếp
a) Cho cos α = 2 3 . Tính giá trị của biểu thức
A = tan α + 3 c o t α tan α + c o t α
b) Cho sin α = 3 5 v à 90 ° < α < 180 °
Tính giá trị của biểu thức:
C = c o t α - 2 tan α tan α + 3 c o t α
Cho góc α thỏa mãn
90
°
α
180
°
,
sin
α
12
13
. Giá trị của cos α là A.
5
13
B.
−
5
13
C.
5
13
D.
25
169
Đọc tiếp
Cho góc α thỏa mãn 90 ° < α < 180 ° , sin α = 12 13 . Giá trị của cos α là
A. 5 13
B. − 5 13
C. 5 13
D. 25 169
Đáp án B
c o s 2 α = 1 − s i n 2 α = 1 − 12 13 2 = 25 169 .
D o 90 ° < α < 180 ° nên cos α < 0 ⇒ cos α = − 5 13
Đúng 0
Bình luận (0)
Cho góc α thỏa mãn
0
α
π
4
và
sin
α
+
cos
α
5
2
. Tính P sinα - cosα A.
P
3
2
B. P 1 C. P -1/2 D.
P
-...
Đọc tiếp
Cho góc α thỏa mãn 0 < α < π 4 và sin α + cos α = 5 2 . Tính P = sinα - cosα
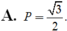 A.
P
=
3
2
A.
P
=
3
2
B. P = 1
C. P = -1/2
D. P = - 3 2
Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do ![]() suy ra sinα < cosα nên sinα - cosα < 0.
suy ra sinα < cosα nên sinα - cosα < 0.
Vậy 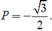
Đúng 0
Bình luận (0)
1. Cho α + β + f π . CM:a1) sinα + sinβ +sinf 4.cosdfrac{alpha}{2} .cosdfrac{beta}{2}. cosdfrac{f}{2}a2) cosα + cosβ +cosf 1+ 4sindfrac{alpha}{2}.sindfrac{beta}{2}.sindfrac{f}{2}Các bạn giúp mình với ạ
Đọc tiếp
1. Cho α + β + f = π . CM:
a1) sinα + sinβ +sinf = 4.cos\(\dfrac{\alpha}{2}\) .cos\(\dfrac{\beta}{2}\). cos\(\dfrac{f}{2}\)
a2) cosα + cosβ +cosf = 1+ 4sin\(\dfrac{\alpha}{2}\).sin\(\dfrac{\beta}{2}\).sin\(\dfrac{f}{2}\)
Các bạn giúp mình với ạ
1.a) \(4cos\dfrac{\alpha}{2}.cos\dfrac{\beta}{2}.cos\dfrac{f}{2}\)
\(=\dfrac{1}{2}.4\left[cos\left(\dfrac{\alpha-\beta}{2}\right)+cos\left(\dfrac{\alpha+\beta}{2}\right)\right].cos\dfrac{f}{2}\)
\(=2.cos\left(\dfrac{\alpha-\beta}{2}\right)cos\dfrac{f}{2}+2.cos\left(\dfrac{\alpha+\beta}{2}\right).cos\dfrac{f}{2}\)
\(=cos\left(\dfrac{\alpha-\left(\beta+f\right)}{2}\right)+cos\left(\dfrac{\alpha-\beta+f}{2}\right)+cos\left(\dfrac{\alpha+\beta-f}{2}\right)+cos\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=cos\left(\dfrac{2\alpha-\pi}{2}\right)+cos\left(\dfrac{\pi-2\beta}{2}\right)+cos\left(\dfrac{\pi-2f}{2}\right)+cos\left(\dfrac{\pi}{2}\right)\)
\(=cos\left(-\dfrac{\pi}{2}+\alpha\right)+cos\left(\dfrac{\pi}{2}-\beta\right)+cos\left(\dfrac{\pi}{2}-f\right)\)
\(=sin\alpha+sin\beta+sinf\) (đpcm)
Đúng 2
Bình luận (1)
a2) \(1+4sin\dfrac{\alpha}{2}.sin\dfrac{\beta}{2}.sin\dfrac{f}{2}\)
\(=1+2\left[cos\left(\dfrac{\alpha-\beta}{2}\right)-cos\left(\dfrac{\alpha+\beta}{2}\right)\right].sin\dfrac{f}{2}\)
\(=1+2.cos\left(\dfrac{\alpha-\beta}{2}\right).sin\dfrac{f}{2}-2.cos\left(\dfrac{\alpha+\beta}{2}\right).sin\dfrac{f}{2}\)
\(=1+sin\left(\dfrac{f-\alpha+\beta}{2}\right)+sin\left(\dfrac{a-\beta+f}{2}\right)-sin\left(\dfrac{f-\left(\alpha+\beta\right)}{2}\right)-sin\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=1+sin\left(\dfrac{\pi-2\alpha}{2}\right)+sin\left(\dfrac{\pi-2\beta}{2}\right)-sin\left(\dfrac{2f-\pi}{2}\right)-sin\left(\dfrac{\pi}{2}\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+sin\left(\dfrac{\pi}{2}-\beta\right)+sin\left(\dfrac{\pi}{2}-f\right)\)
\(=cos\alpha+cos\beta+cosf\) (đpcm)
Đúng 2
Bình luận (0)
Hãy nêu định nghĩa của sinα , cosα và giải thích vì sao ta có:
sin(α +k2 π)=sinα;k ∈Z
cos(α +k2 π)=cosα;k ∈Z
+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
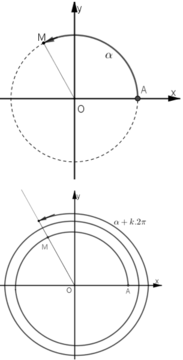
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα
Đúng 0
Bình luận (0)
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Đúng 2
Bình luận (0)
Chứng minh các biểu thức sau không phụ thuộc vào α
A=(sinα+cosα)2+(sinα−cosα)2
B=sin4α(1+2cos2α)+cos4α(1+2sin2α)
C=sin4α(3−2sin2α)+cos4α(3−2cos2α)
Giúp tớ điii
\(A=\left(\sin\alpha+\cos\alpha+\sin\alpha-\cos\alpha\right)^2-2\left(\sin\alpha+\cos\alpha\right)\left(\sin\alpha-\cos\alpha\right)\)
\(=4\sin^2\alpha-2\sin^2\alpha+2\cos^2\alpha=2\left(\sin^2\alpha+\cos^2\alpha\right)=2\)
\(B=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2-1=0\)
\(C=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\)
\(=3\left(\sin^2\alpha+\cos^2\alpha-\frac{1}{9}\right)^2-\frac{1}{9}=\frac{61}{27}\)
Đúng 0
Bình luận (0)
A = \(\dfrac{\text{sinα + cosα}}{\text{sinα - cosα}}\) Tính α biết tan α = \(\sqrt{3}\)
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}{\dfrac{sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{tana+1}{tana-1}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}\)
Đúng 1
Bình luận (0)