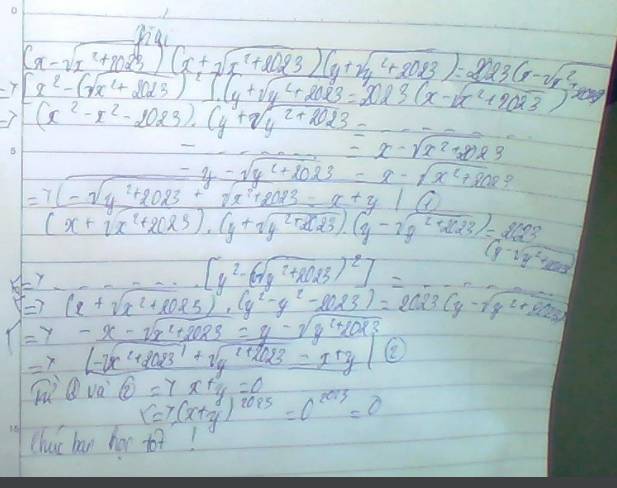gpt: \(2\sqrt[2023]{\left(1+x\right)^2}+3\sqrt[2023]{1-x^2}+\sqrt[2023]{\left(1-x\right)^2}=0\)
NM
Những câu hỏi liên quan
Cho \(\left(x+\sqrt{x^2+2023}\right)\left(y+\sqrt{y^2+2023}\right)=2023
\)
Tính (x+y)2023
Helpppppppppp
Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức. Trước tiên, ta mở đuôi công thức:(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)Từ phép nhân đầu tiên, ta có:(x+y)(x+y) = x^2 + 2xy + y^2Tiếp tục nhân với (x+y), ta có:(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3Lặp lại quá trình này 2020 lần nữa, ta có:(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4Tiếp tục nhân với (x+y), ta có:(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3
Đúng 0
Bình luận (2)
Để tính (x+y)2023, ta sẽ sử dụng công thức nhân đa thức.
Trước tiên, ta mở đuôi công thức:
(x+y)2023 = (x+y)(x+y)(x+y)...(x+y)
Từ phép nhân đầu tiên, ta có:
(x+y)(x+y) = x^2 + 2xy + y^2
Tiếp tục nhân với (x+y), ta có:
(x^2 + 2xy + y^2)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3
Lặp lại quá trình này 2020 lần nữa, ta có:
(x^3 + 3x^2y + 3xy^2 + y^3)(x+y) = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4
Tiếp tục nhân với (x+y), ta có:
(x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4)(x+y) = x^5 + 5x^4y + 10x^3
Đúng 0
Bình luận (0)
Cho \(\left(x+\sqrt{x^2+2023}\right)\left(y+\sqrt{y^2+2023}\right)=2023\)
Tính (x+y)2023
Help me plsss
Tính giá trị của biểu thức \(B=\dfrac{4x^{2024}\left(x+1\right)-2x^{2023}+2x+1}{2x^2+3x}\) tại \(x=\sqrt{\dfrac{1}{2\sqrt{3}}-\dfrac{3}{2\sqrt{3}+2}}\)
\(x=\sqrt{\dfrac{2\sqrt{3}+2-6\sqrt{3}}{2\sqrt{3}\left(2\sqrt{3}+2\right)}}=\sqrt{\dfrac{2-4\sqrt{3}}{2\sqrt{3}\left(2\sqrt{3}+2\right)}}\) ko tồn tại vì 2-4căn 3<0
Đúng 0
Bình luận (0)
cho các số thực x,y,z thỏa mãn \(\left(x-y +z\right)^2\)+\(\sqrt{y^4}\)+\(\left|1-z^3\right|\) \(\le\) 0
Chứng minh rằng \(x^{2023}\)+\(y^{2024}\)+\(z^{2025}\)=0
Lời giải:
Ta thấy, với mọi $x,y,z$ là số thực thì:
$(x-y+z)^2\geq 0$
$\sqrt{y^4}\geq 0$
$|1-z^3|\geq 0$
$\Rightarrow (x-y+z)^2+\sqrt{y^4}+|1-z^3|\geq 0$ với mọi $x,y,z$
Kết hợp $(x-y+z)^2+\sqrt{y^4}+|1-z^3|\leq 0$
$\Rightarrow (x-y+z)^2+\sqrt{y^4}+|1-z^3|=0$
Điều này xảy ra khi: $x-y+z=y^4=1-z^3=0$
$\Leftrightarrow y=0; z=1; x=-1$
Đúng 3
Bình luận (0)
a) cho C = 3 - \(3^2+3^3-3^4+3^5-3^6+...+3^{23}-3^{24}\), chứng minh rằng C \(⋮\) 420
b) tìm x và y biết \(\left(x+1\right)^{2022}+\left(\sqrt{y-1}\right)^{2023}=0\)
Tìm giá trị nhỏ nhất cảu biểu thức : \(x^2+2xy+2y^2+2\sqrt{2}x+2\left(\sqrt{2}+1\right)y+2023\)
a, cho a, b là 2 số thoả mãn |a-2b+3|^{2023} + (b-1)^{2024} 0. Tính giá trị biểu thứcP a^{2023} x b^{2024} + 2024b, 3 số hữu tỉ x,y,z thoả mãn xy+yz+zx 2023. Chứng tỏ rằng:A dfrac{left(x^2+2023right)xleft(y^2+2023right)xleft(z^2+2023right)}{16} viết được dưới dạng bình phương của 1 số hữu tỉ
Đọc tiếp
a, cho a, b là 2 số thoả mãn |a-2b+3|\(^{2023}\) + (b-1)\(^{2024}\) = 0. Tính giá trị biểu thức
P = a\(^{2023}\) x b\(^{2024}\) + 2024
b, 3 số hữu tỉ x,y,z thoả mãn xy+yz+zx = 2023. Chứng tỏ rằng:
A = \(\dfrac{\left(x^2+2023\right)x\left(y^2+2023\right)x\left(z^2+2023\right)}{16}\) viết được dưới dạng bình phương của 1 số hữu tỉ
a: \(\left|a-2b+3\right|^{2023}>=0\forall a,b\)
\(\left(b-1\right)^{2024}>=0\forall b\)
Do đó: \(\left|a-2b+3\right|^{2023}+\left(b-1\right)^{2024}>=0\forall a,b\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a-2b+3=0\\b-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=1\\a=2b-3=2\cdot1-3=-1\end{matrix}\right.\)
Thay a=-1 và b=1 vào P, ta được:
\(P=\left(-1\right)^{2023}\cdot1^{2024}+2024=2024-1=2023\)
Đúng 0
Bình luận (0)
|1-\(\sqrt{23}\)|+23-\(\sqrt{23}\)-\(\left|-2023\right|^0\)
Lời giải:
$|1-\sqrt{23}|+23-\sqrt{23}-|-2023|^0=\sqrt{23}-1+23-\sqrt{23}-1$
$=23-2=21$
Đúng 0
Bình luận (0)
Cho a,b,c là các số hữu tỉ t/m ab+bc+ca = 2023
CMR: A=\(\sqrt{a^2+2023\left(b^2+2023\right)\left(c^2+2023\right)}\) cùng là số hữu tỉ
Ta có: `a^2+2023=a^2+ab+bc+ca=a(a+b)+c(a+b)=(a+b)(c+a)`
Do vai trò ba biến `a,b,c` như nhau nên ta có: `b^2+2023=(b+c)(a+b);c^2+2023=(c+a)(b+c)`
`=>A=\sqrt(((a+b)(b+c)(c+a))^2)=|(a+b)(b+c)(c+a)|\inQQ`
Đúng 1
Bình luận (1)
Ta có: a2+2023 = a2+ab+bc+ca
= a(a+b) + c(b+a)
= (a+b)(a+c)
CM tương tự ta đc: b2+2023= (b+c)(b+a)
c2+2023 = (c+a)(c+b)
Ta được: A= \(\sqrt{\left(a+b\right)\left(a+c\right)\left(b+c\right)\left(b+a\right)\left(c+a\right)\left(c+b\right)}\) A= \(\sqrt{\left(a+b\right)^2\left(a+c\right)^2\left(b+c\right)^2}\)
A= \(\left|\left(a+b\right)\left(a+c\right)\left(b+c\right)\right|\)
Vì a,b,c là các số hữu tỉ (đb) nên (a+b)(a+c)(b+c) là các số hữu tỉ (đpcm)
Đúng 1
Bình luận (1)
Cho a-b=\(\sqrt{29+12\sqrt{5}}\) -\(2\sqrt{5}\)
Giá trị biểu thức \(a^2\left(a+1\right)-b^2\left(b-1\right)-11ab+2024\) bằng
A.2023 B.2035 C.2060 D.2027
Ta có: \(a^2\left(a+1\right)-b^2\left(b-1\right)-11ab+2024\) (1)
Lại có: \(a-b=\sqrt{29+12\sqrt{5}}-2\sqrt{5}\)
\(=\sqrt{\left(2\sqrt{5}\right)^2+2\cdot2\sqrt{5}\cdot3+3^2}-2\sqrt{5}\)
\(=\sqrt{\left(2\sqrt{5}+3\right)^2}-2\sqrt{5}\)
\(=2\sqrt{5}+3-2\sqrt{5}\)
\(=3\)
\(\Rightarrow a=b+3\)
Thay \(a=b+3\) vào (1), ta được:
\(\left(b+3\right)^2\left(b+3+1\right)-b^2\left(b-1\right)-11\left(b+3\right)b+2024\)
\(=\left(b^2+6b+9\right)\left(b+4\right)-b^3+b^2-11b^2-33b+2024\)
\(=b\left(b^2+6b+9\right)+4\left(b^2+6b+9\right)-b^3-10b^2-33b+2024\)
\(=b^3+6b^2+9b+4b^2+24b+36-b^3-10b^2-33b+2024\)
\(=\left(b^3-b^3\right)+\left(6b^2+4b^2-10b^2\right)+\left(9b+24b-33b\right)+\left(2024+36\right)\)
\(=2060\)
$\Rightarrow$ Chọn đáp án $C$.
Đúng 2
Bình luận (0)
Ta có : \(a-b=\sqrt{29+12\sqrt{5}}-2\sqrt{5}\)
\(\Rightarrow a-b=\sqrt{20+12\sqrt{5}+9}-2\sqrt{5}\)
\(\Rightarrow a-b=\sqrt{\left(2\sqrt{5}+3\right)^2}-2\sqrt{5}\)
\(\Rightarrow a-b=2\sqrt{5}+3-2\sqrt{5}\)
\(\Rightarrow a-b=3\)
Xét biểu thức : \(a^2\left(a+1\right)-b^2\left(b-1\right)-11ab+2024\)
\(=a^3+a^2-b^3+b^2-11ab+2024\)
\(=a^3-b^3+a^2+b^2-2ab-9ab+2024\)
\(=a^3-b^3-9ab+a^2-2ab+b^2+2024\)
\(=a^3-3ab\left(a-b\right)-b^3+\left(a-b\right)^2+2024\) vì \(a-b=3\)
\(=\left(a-b\right)^3+\left(a-b\right)^2+2024\)
\(=3^3+3^2+2024\)
\(=2060\)
\(\Rightarrow C\)
Đúng 0
Bình luận (0)