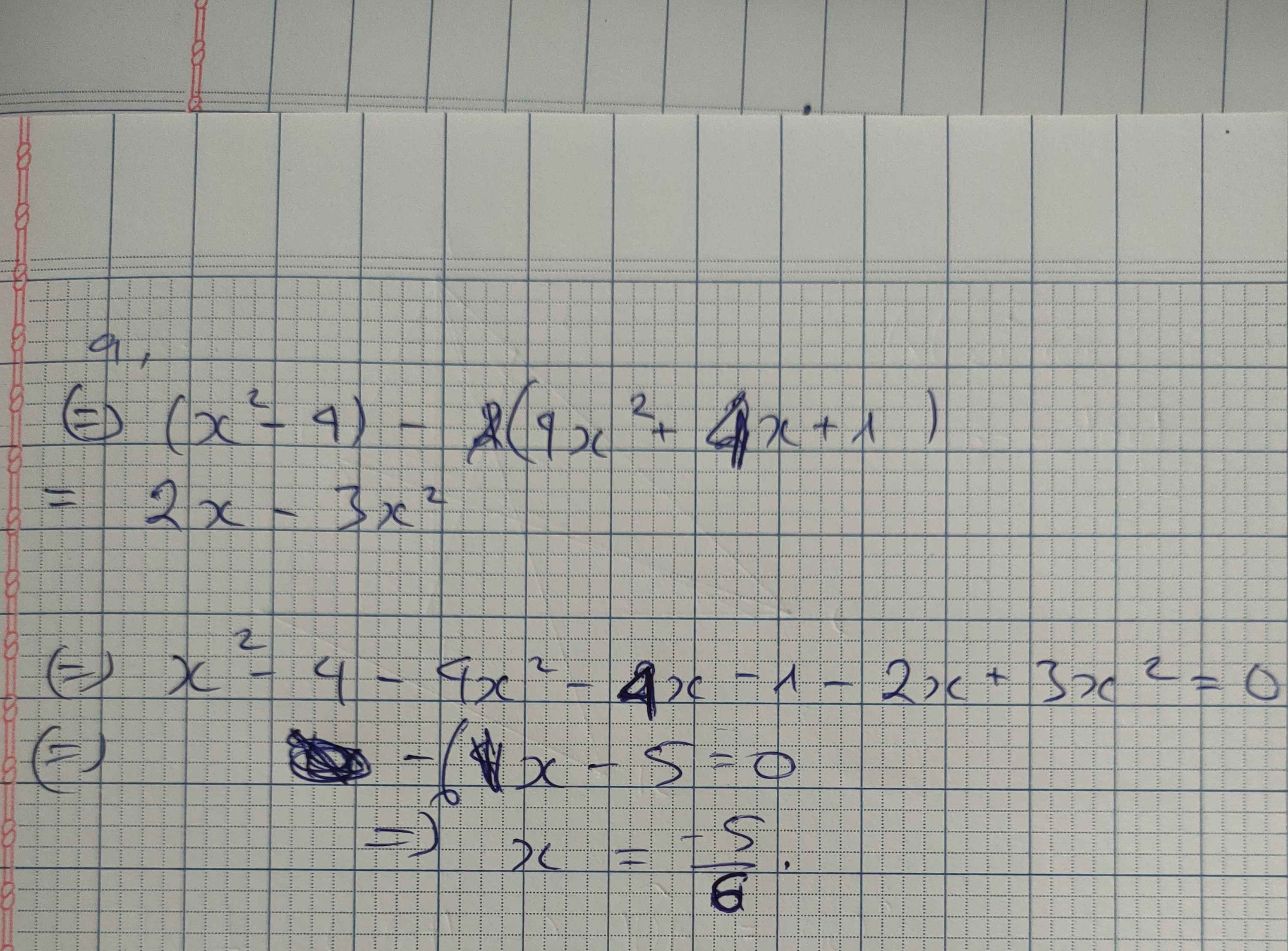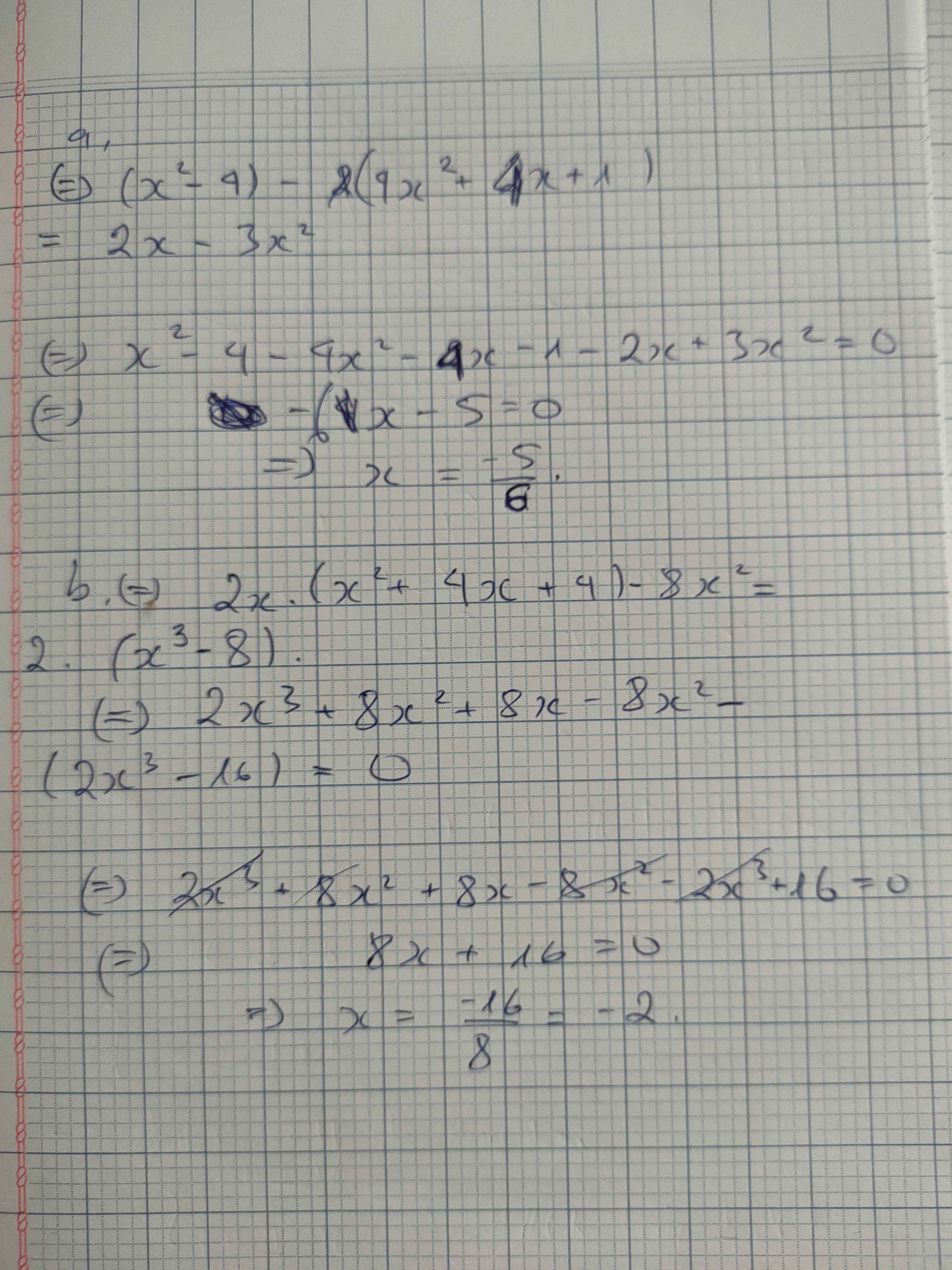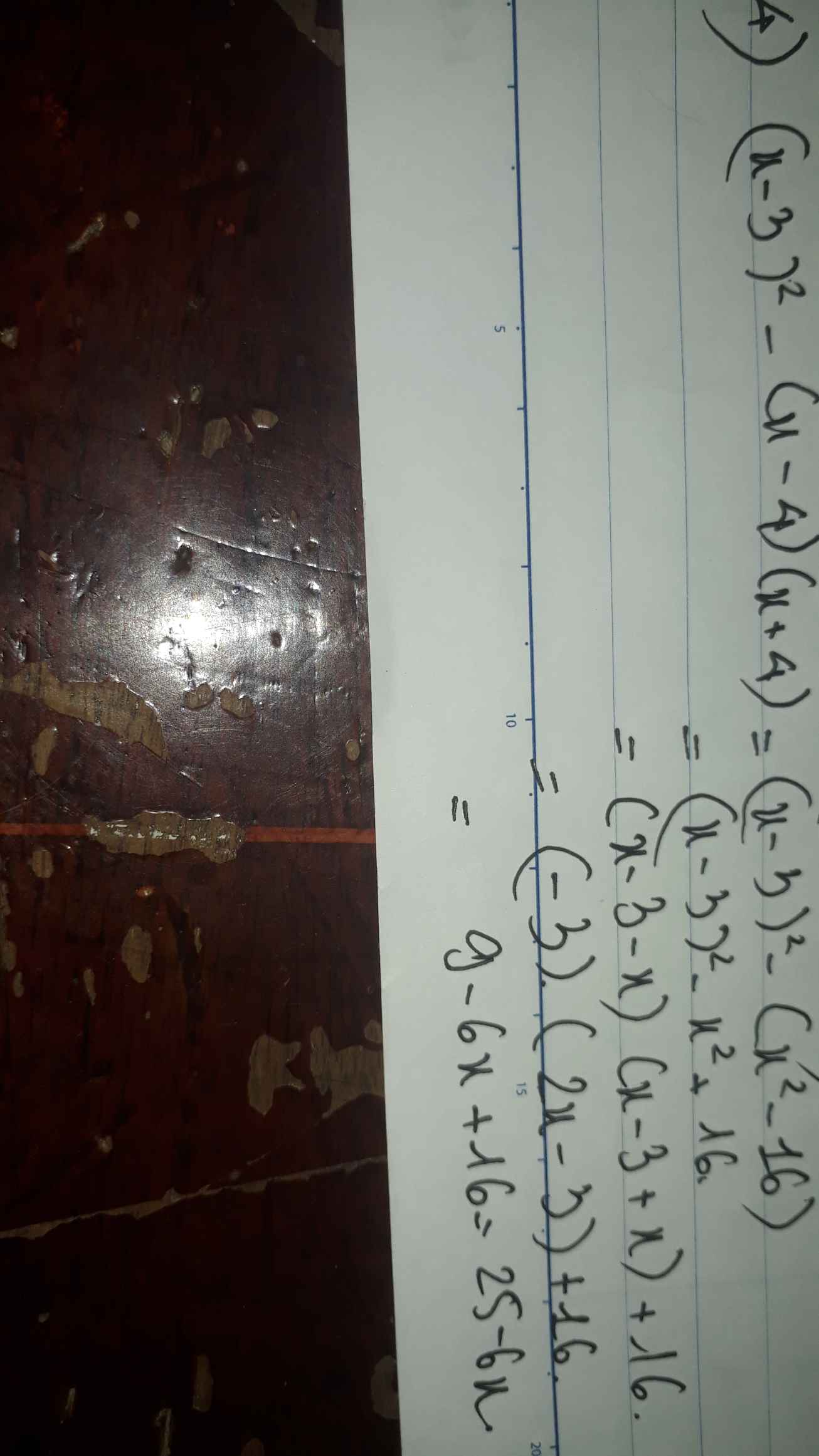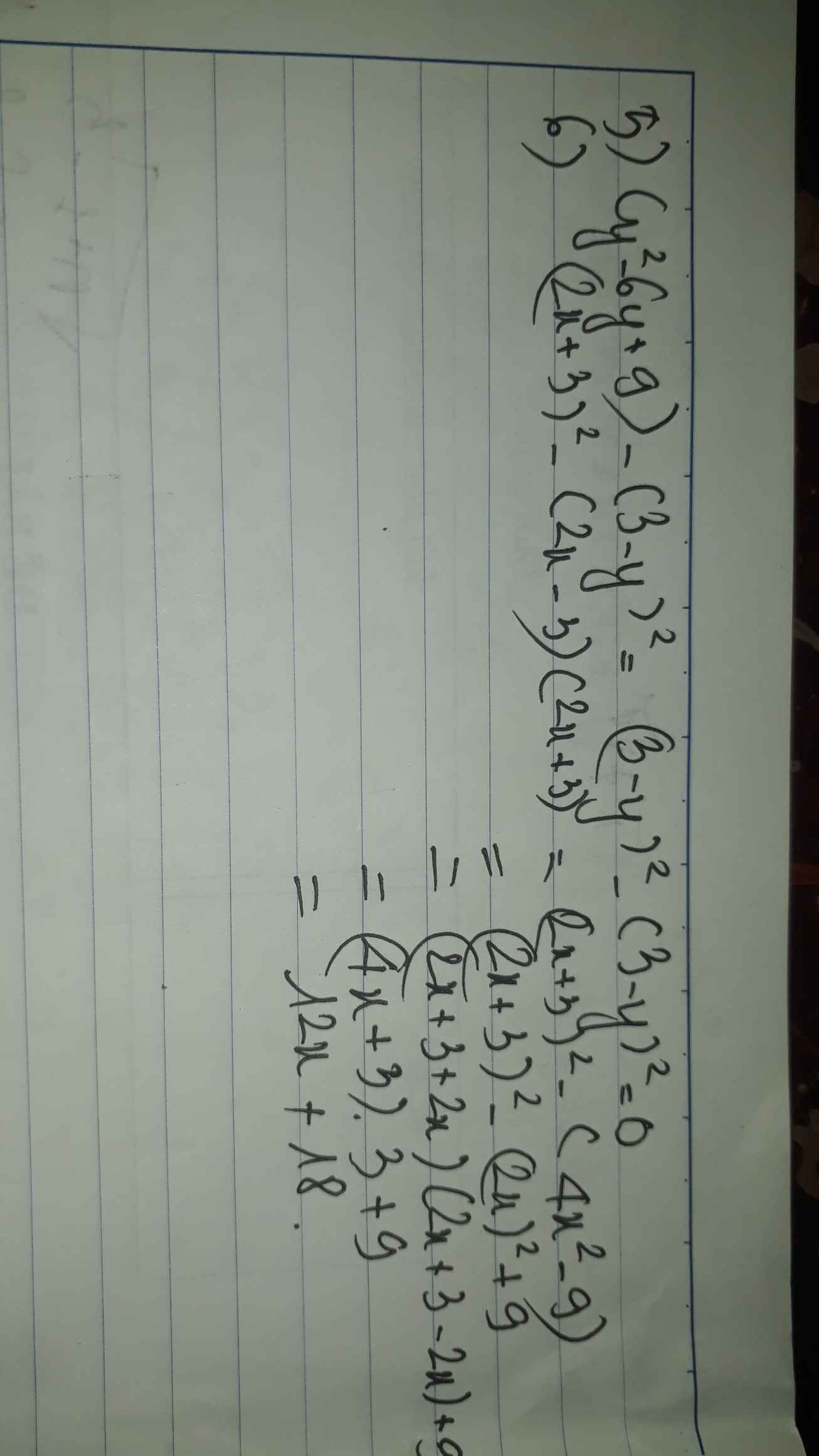1)

x^3 -16x=0`

`<=>x(x^2 -16)=0`

\(< =>\left[{}\begin{matrix}x=0\\x^2-16=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x^2=16\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)

b)

`x^4 -2x^3=0`

`<=>x^3 (x-2)=0`

\(< =>\left[{}\begin{matrix}x^3=0\\x-2=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

3)

`(2x-11)(x^2 -1)=0`

\(< =>\left[{}\begin{matrix}2x-11=0\\x^2-1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}2x=11\\x^2=1\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{11}{2}\\x=1\\x=-1\end{matrix}\right.\)

4)

`x^3 -36x=0`

`<=>x(x^2 -36)=0`

\(< =>\left[{}\begin{matrix}x=0\\x^2-36=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x^2=36\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=6\\x=-6\end{matrix}\right.\)

5)

`2x+19=0`

`<=>2x=-19`

`<=>x=-19/2`

bài về nghiệm của đa thức

1) Ta có: \(\left(x+2\right)^2+\left(x-3\right)^2\)

\(=x^2+4x+4+x^2-6x+9\)

\(=2x^2-2x+13\)

2) Ta có: \(\left(4-x\right)^2-\left(x-3\right)^2\)

\(=\left(4-x-x+3\right)\left(4-x+x-3\right)\)

\(=-2x+7\)

3) Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x+5\right)^2\)

\(=x^2-25-x^2-10x-25\)

=-10x-50

4) Ta có: \(\left(x-3\right)^2-\left(x-4\right)\left(x+4\right)\)

\(=x^2-6x+9-x^2+16\)

=-6x+25

5) Ta có: \(\left(y^2-6y+9\right)-\left(y-3\right)^2\)

\(=y^2-6y+9-y^2+6y-9\)

=0

6) Ta có: \(\left(2x+3\right)^2-\left(2x-3\right)\left(2x+3\right)\)

\(=4x^2+12x+9-4x^2+9\)

=12x+18

1) 2x – (3 – 5x) = 4( x +3)

<=>2x-3+5x=4x+12

<=>2x-3+5x-4x-12=0

<=>3x-15=0

<=>x=5

2) 5(2x-3) - 4(5x-7) =19 - 2(x+11)

<=>10x-15-20x+28=19-2x-22

<=>10x-15-20x+28-19+2x+22=0

<=>-8x+16=0

<=>x=2

tham khảo

1) 2x – (3 – 5x) = 4( x +3)

<=>2x-3+5x=4x+12

<=>2x-3+5x-4x-12=0

<=>3x-15=0

<=>x=5

2) 5(2x-3) - 4(5x-7) =19 - 2(x+11)

<=>10x-15-20x+28=19-2x-22

<=>10x-15-20x+28-19+2x+22=0

<=>-8x+16=0

<=>x=2

A,

a: \(\Leftrightarrow x^2-4-4x^2-4x-1-2x+3x^2=0\)

=>-6x-5=0

=>-6x=5

hay x=-5/6

b: \(\Leftrightarrow2x^3+8x^2+8x-8x^2-2x^3+16=0\)

=>8x+16=0

hay x=-2

c: \(\Leftrightarrow x^3-6x^2+12x-8+9x^2-1-x^3-3x^2-3x-1=0\)

=>9x-10=0

hay x=10/9

d: \(\Leftrightarrow10x-15-20x+28=19-2x^2-4x-2\)

\(\Leftrightarrow-10x+13+2x^2+4x-17=0\)

\(\Leftrightarrow2x^2-6x-4=0\)

\(\Leftrightarrow x^2-3x-2=0\)

\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-2\right)=9+8=17>0\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{17}}{2}\\x_2=\dfrac{3+\sqrt{17}}{2}\end{matrix}\right.\)

1) Ta có: \(\left(x+2\right)^2+\left(x-3\right)^2\)

\(=x^2+4x+4+x^2-6x+9\)

\(=2x^2-2x+13\)

2) Ta có: \(\left(4-x\right)^2-\left(x-3\right)^2\)

\(=\left(4-x-x+3\right)\left(4-x+x-3\right)\)

\(=\left(-2x+7\right)\cdot1\)

\(=-2x+7\)

3) Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x+5\right)^2\)

\(=x^2-25-x^2-10x-25\)

\(=-10x-50\)

`Answer:`

a. \(x^3+6x^2+12=19\)

\(\Leftrightarrow x^3+6x^2+12x-19=0\)

\(\Leftrightarrow x^3-x^2+7x^2-7x+19x-19=0\)

\(\Leftrightarrow x^2.\left(x-1\right)+7x\left(x-1\right)+19\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2+7x+19\right)=0\)

Ta có \(x^2+7x+19=x^2+2x.3,5+12,25+6,75=\left(x+3,5\right)^2+6,75>0\)

\(\Rightarrow x-1=0\Leftrightarrow x=1\)

b. \(5\left(x+9\right)^2.\left(x-4\right)^3-10\left(x+9\right)^3.\left(x-4\right)^2=0\)

\(\Leftrightarrow5\left(x+9\right)^2.\left(x-4\right)^2.[x-4-2\left(x+9\right)]=0\)

\(\Leftrightarrow\left(x+9\right)^2.\left(x-4\right)^2.\left(x-4-2x-18\right)=0\)

\(\Leftrightarrow\left(x+9\right)^2.\left(x-4\right)^2.\left(-x-22\right)=0\)

\(\Leftrightarrow\left(x+9\right)^2=0\) hoặc \(\left(x-4\right)^2=0\) hoặc \(-x-22=0\)

\(\Leftrightarrow x+9=0\) hoặc \(x-4=0\) hoặc \(-x=22\)

\(\Leftrightarrow x=-9\) hoặc \(x=4\) hoặc \(x=-22\)

c. \(\left(2x+3\right)^2+\left(x-2\right)^2-2\left(2x+3\right)\left(x-2\right)\)

\(=\left(2x+3\right)^2-2\left(2x+3\right)\left(x-2\right)+\left(x-2\right)^2\)

\(=\left(2x+3-x+2\right)^2\)

\(=\left(x+5\right)^2\)

a)x=4-12=-8

b)x=19-0=19

c)x=-12+4:2=-4

d)x=6+(-2):2=2

`#3107.101107`

\(x(x+5)(x-5) - (x+2)(x^2-2x+4)=5\)

`<=> x(x^2 - 25) - (x^3 + 2^3) = 5`

`<=> x^3 - 25x - x^3 - 8 = 5`

`<=> -25x - 8 = 5`

`<=> -25x = 13`

`<=> x = -13/25`

Vậy, `x = -13/25`

_____

\((x+1)^3 - (x-1)^3 -6(x-1)^2 = -19\)

`<=> x^3 + 3x^2 + 3x + 1 - (x^3 - 3x^2 + 3x - 1) - 6(x^2 - 2x + 1) = -19`

`<=> x^3 + 3x^2 + 3x + 1 - x^3 + 3x^2 - 3x + 1 - 6x^2 + 12x - 6 = -19`

`<=> (x^3 - x^3) + (3x^2 + 3x^2 - 6x^2) + (3x - 3x + 12x) + (1 + 1 - 6) = -19`

`<=> 12x - 4 = -19`

`<=> 12x = -15`

`<=> x = -15/12 = -5/4`

Vậy, `x = -5/4.`

________

`@` Sử dụng các hđt:

`1)` `A^2 + B^2 = (A - B)(A + B)`

`2)` `A^3 + B^3 = (A + B)(A^2 - AB + B^2)`

`3)` `(A - B)^3 = A^3 - 3A^2B + 3AB^2 - B^3`

`4)` `(A + B)^3 = A^3 + 3A^2B + 3AB^2 + B^3`

`5)` `(A - B)^2 = A^2 - 2AB + B^2.`

a: \(x\left(x+5\right)\left(x-5\right)-\left(x+2\right)\left(x^2-2x+4\right)=5\)

=>\(x\left(x^2-25\right)-x^3-8=5\)

=>\(x^3-25x-x^3-8=5\)

=>-25x=13

=>\(x=-\dfrac{13}{25}\)

b: \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-19\)

=>\(x^3+3x^2+3x+1-x^3+3x^2-3x+1-6\left(x^2-2x+1\right)=-19\)

=>\(6x^2+2-6x^2+12x-6=-19\)

=>12x-4=-19

=>12x=-15

=>x=-5/4