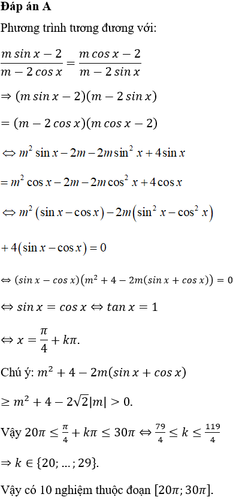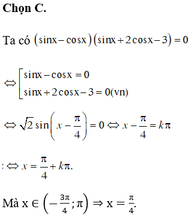Phương trình \(sin3x=-sinx\) có bao nhiêu nghiệm thuộc đoạn \(\left[0;100\pi\right]\) ?
H24
Những câu hỏi liên quan
Số điểm biểu diễn các nghiệm của phương trình sin3x - cos3x + căn3 0 trên đường tròn lượng giác? Nghiệm của phương trình sinx căn2 Phương trình sin2x (căn3)/2 có bao nhiêu nghiệm trên đoạn [-pi; 2pi] Trong mặt phẳng tọa độ Oxy Tìm ảnh đường tròn C: x² + y² - 4y + 6y - 12. Qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 độ và phép vị tự tâm O tỉ số k 2
Đọc tiếp
Số điểm biểu diễn các nghiệm của phương trình sin3x - cos3x + căn3 = 0 trên đường tròn lượng giác?
Nghiệm của phương trình sinx = căn2 Phương trình sin2x = (căn3)/2 có bao nhiêu nghiệm trên đoạn [-pi; 2pi]
Trong mặt phẳng tọa độ Oxy Tìm ảnh đường tròn C: x² + y² - 4y + 6y - 12. Qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O góc quay 90 độ và phép vị tự tâm O tỉ số k = 2
Cho phương trình:
(
sin
x
+
sin
3
x
+
cos
3
x
1
+
2
sin
2
x
)
3
+
cos
2
x
5...
Đọc tiếp
Cho phương trình: ( sin x + sin 3 x + cos 3 x 1 + 2 sin 2 x ) = 3 + cos 2 x 5 . Các nghiệm của phương trình thuộc khoảng ( 0 ; 2 π ) là:
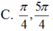
Vì các nghiệm của phương trình thuộc khoảng
(
0
;
2
π
)
nên nghiệm của phương trình là 
Đúng 0
Bình luận (0)
BT
6 tháng 12 2016 lúc 23:05
số nghiệm của phương trình \(\frac{\sin3x}{\cos x+1}=0\) thuộc đoạn \(\left[2\pi;4\pi\right]\)là bao nhiêu ?
Phương trình sin 3 x + cos 2 x – sin x = 0 có tập nghiệm (0; π) là:
A. {π/4;3π/4}
B. {π/4}
C. {3π/4}
D. {π/6;π/4;3π/4}
Chọn A
Ta có sin3x+ cos2x- sinx= 0 ⇔ cos2x(2sinx+1)=0. Lưu ý trong khoảng (0;π), sinx > 0
Đúng 0
Bình luận (0)
Khi
m
≠
0
,
m
≠
±
2
phương trình
m
sin
x
-
2
m
-
2
cos
x
m
cos
x
-
2
m...
Đọc tiếp
Khi m ≠ 0 , m ≠ ± 2 phương trình m sin x - 2 m - 2 cos x = m cos x - 2 m - 2 sin x có bao nhiêu nghiệm thuộc đoạn [ 20 π ; 30 π ] ?
A. 10.
B. 9.
C. 20.
D. 18.
Có bao nhiêu giá trị thực của m để phương trình
sin
x
-
1
2
cos
2
x
-
2
m
+
1
cos
x
+
m...
Đọc tiếp
Có bao nhiêu giá trị thực của m để phương trình sin x - 1 2 cos 2 x - 2 m + 1 cos x + m =0 có đúng bốn nghiệm thực phân biệt thuộc đoạn 0 ; 2 π ?
A. 3
B. 1
C. 2
D. 4
H24
7 tháng 10 2021 lúc 9:11
Phương trình sin3x = −sin x có bao nhiêu nghiệm thuộc đoạn [0;100π] ?
A. 300 B. 101 C. 299 D. 301
Lời giải:
\(\sin 3x=-\sin x=\sin (-x)\)
\(\Leftrightarrow \left[\begin{matrix} 3x=-x+2k\pi\\ 3x=\pi +x+2t\pi\end{matrix}\right.\) với $t,k$ nguyên bất kỳ
\(\Leftrightarrow \left[\begin{matrix} x=\frac{k\pi}{2}\\ x=\frac{(2t+1)\pi}{2}\end{matrix}\right.\) với $k,t$ nguyên bất kỳ
Để $x\in [0; 100\pi]$ thì \(\left\{\begin{matrix} 0\leq \frac{k}{2}\leq 100\\ 0\leq \frac{2t+1}{2}\leq 100\end{matrix}\right.\)
Vì $t,k$ nguyên nên:
$k\in \left\{0;1;2;...;200\right\}$ $\rightarrow 201$ giá trị
$t\in \left\{0;1;2;,,,;99\right\}$ $\rightarrow 100$ giá trị
Vậy có: $201+100=301$ nghiệm.
Đúng 1
Bình luận (1)
Phương trình (sinx - cosx)(sinx + 2cosx - 3) 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng
-
3
π
4
;
π
? A. 3 B. 0. C. 1. D. 2.
Đọc tiếp
Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng - 3 π 4 ; π ?
A. 3
B. 0.
C. 1.
D. 2.
JP
7 tháng 9 2023 lúc 21:25
Phương trình \(\left(2cos2x-\pi\right)\left(sinx-cosx\right)=0\) có số nghiệm thuộc đoạn \(\left[-\pi;\pi\right]\) là
A. 4
B. 5
C. 3
D. 2
=>2cos2x=pi(loại) hoặc sin x-cosx=0
=>sin x-cosx=0
=>sin(x-pi/4)=0
=>x-pi/4=kpi
=>x=kpi+pi/4
mà x\(\in\left[-pi;pi\right]\)
nên \(x\in\left\{\dfrac{pi}{4};-\dfrac{3}{4}pi\right\}\)
=> D
Đúng 0
Bình luận (1)
cho phương trình \(2cos2x+sin^2xcosx+sinxcos^2x=m\left(sinx+cosx\right)\)tìm m để phương trình có ít nhất 1 nghiệm thuộc đoạn\(\left[0;\dfrac{\Pi}{2}\right]\)
\(\Leftrightarrow2\left(cos^2x-sin^2x\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left(2cosx-2sinx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(\text{vô nghiệm trên đoạn xét}\right)\\2cosx-2sinx+sinx.cosx=m\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(t=cosx-sinx=\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}t\in\left[-1;1\right]\\sinx.cosx=\dfrac{1-t^2}{2}\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2t+\dfrac{1-t^2}{2}=m\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+2t+\dfrac{1}{2}\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=2\notin\left[-1;1\right]\) ; \(f\left(-1\right)=-2\) ; \(f\left(1\right)=2\)
\(\Rightarrow-2\le f\left(t\right)\le2\Rightarrow-2\le m\le2\)
Đúng 0
Bình luận (0)