Làm giúp mình câu a,b với ạ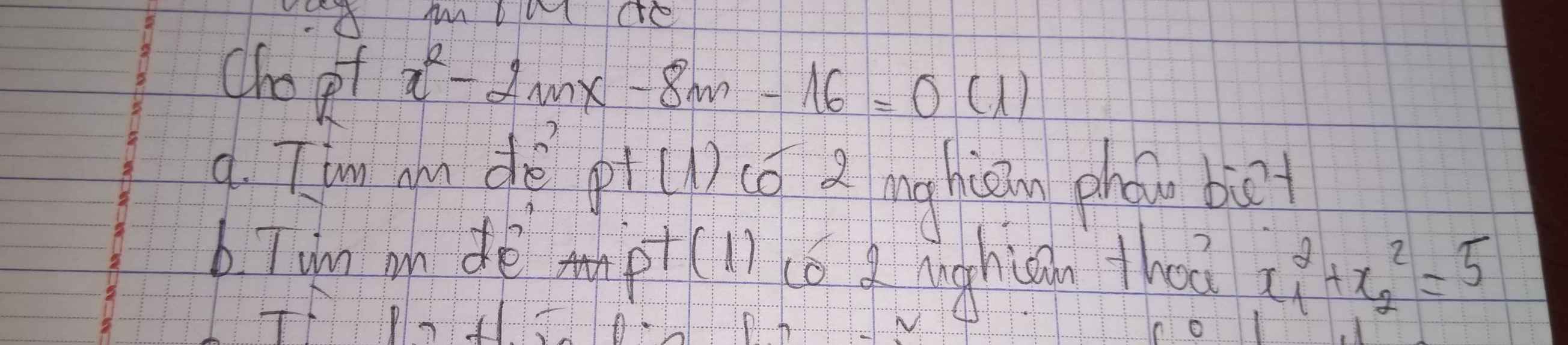
SM
Những câu hỏi liên quan
Mong các bạn giải giúp mình câu b với ạ! ( câu b mình làm không đúng đâu )
Còn câu a là thầy giáo mình đã chữa.
Cảm ơn các bạn nhiều ạ !!!


Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
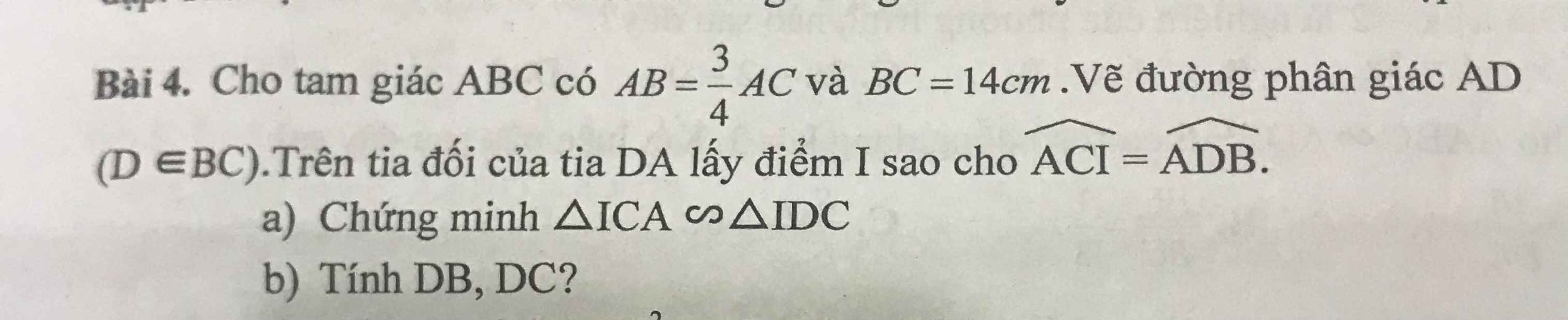
Làm giúp mình câu b với ạ. Mình xin cảm ơn
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm
Đúng 0
Bình luận (0)
giúp mình làm chi tiết câu b với ạ
b: ΔOAH cân tại O(Do A,H cùng nằm trên (O))
mà OD là đường cao
nên OD là phân giác của góc AOH
Xét ΔOAD và ΔOHD có
OA=OH
góc AOD=góc HOD
OD chung
Do đó: ΔOAD=ΔOHD
=>góc OHD=góc OAD=90 độ
=>DH vuông góc OH
Đúng 1
Bình luận (1)

mọi người giúp mình câu b, c,d với ạ đừng làm thiếu nha mình đnag cần gấp mình cám ơn rất nhiều ạ
Ai biết làm câu 7 với câu 9 kh ạ ? Giúp mình với ạ
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
Các bạn giúp mình câu b;c;d;e ạ. Các bạn làm được câu nào thì làm ạ, còn bạn nào giỏi giúp mình nhiều hơn thì tốt ạ! 

làm giúp mình câu 5 :câu 3 với!giải dõ hộ mình với ạ!
Câu 1: D
Câu 2: C
Câu 3: C
Câu 4: D
Câu 5: A
Đúng 0
Bình luận (1)





