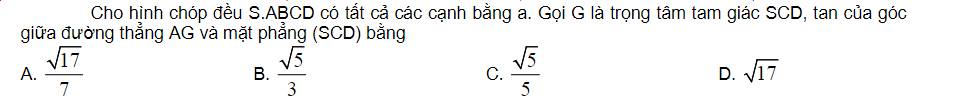
dựa vào dạng toán: Góc giữa đường thẳng và mặt phẳng trong chương trình toán 11.
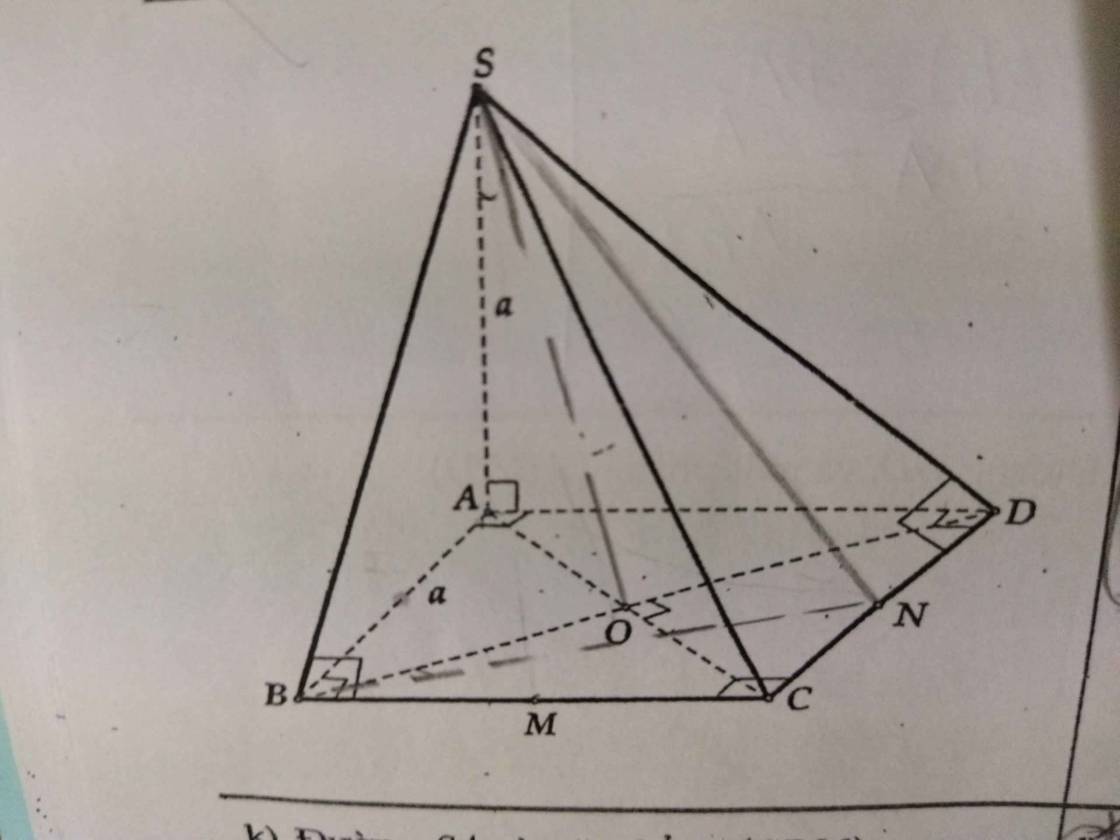
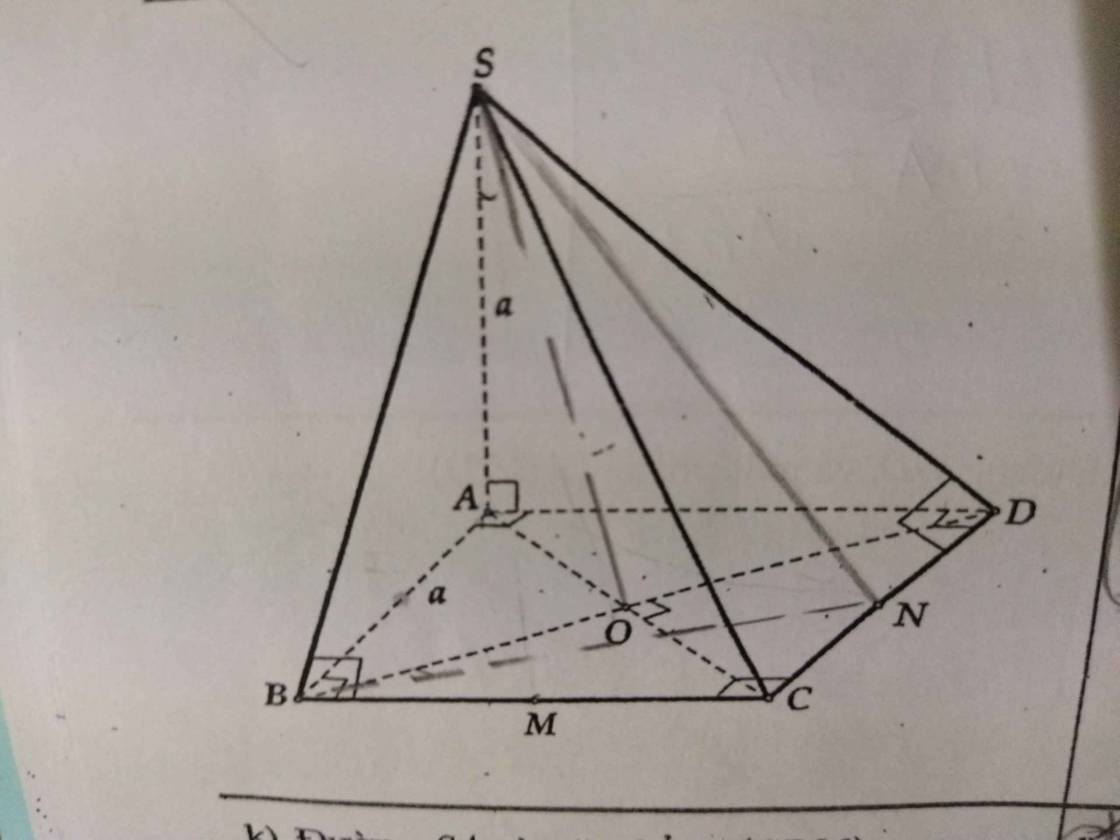
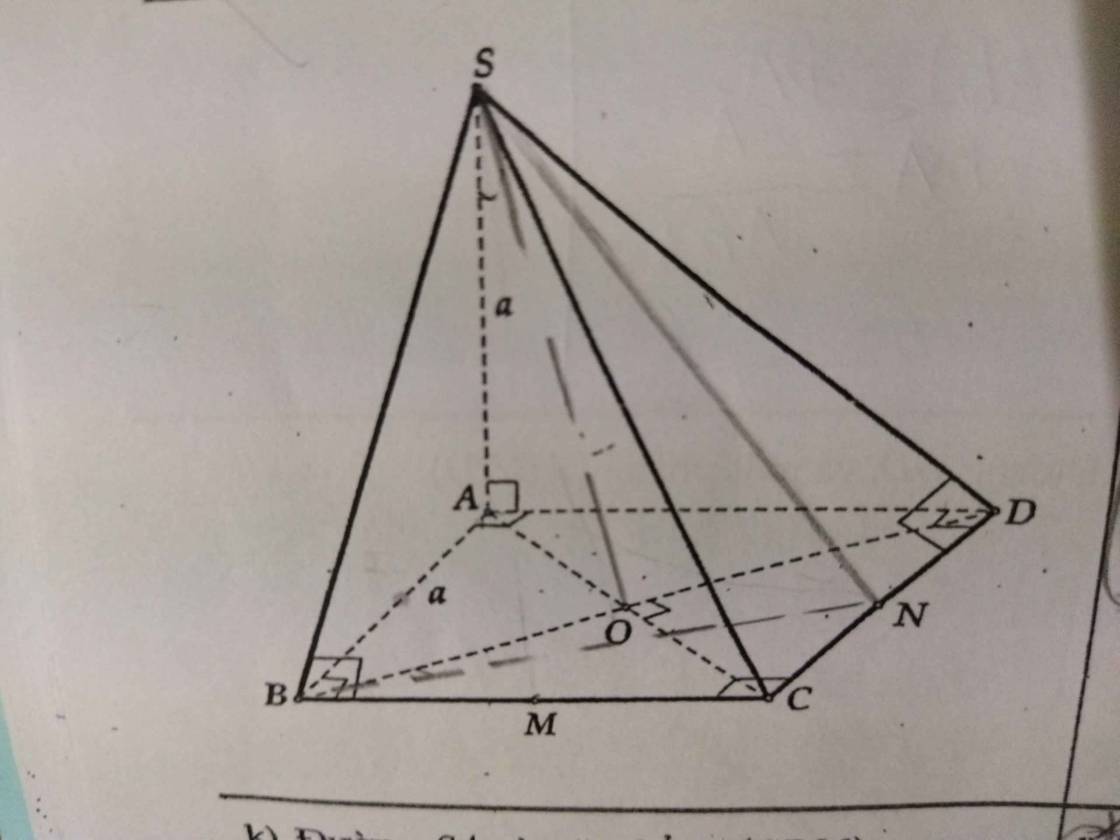
Cho hình chóp S.ABCD tâm O, cạnh ạ, SA vuông (ABCD) và SA= a. Gọi M, N lần lượt là trung điểm của các cạnh BC và DC. Xác định và tính góc giữa: Đường SA và mặt phẳng (SBN). Gợi ý: dựng đường vuông góc bên ngoài vào để chứng minh