Cho tam giác DEF vuông tại D biết DE=3cm,DF=4cm.Kẻ đường trung tuyến DM (M€EF).Tính độ dài EF,DM
H24
Những câu hỏi liên quan
cho tam giác DEF cân tại D,đường trung tuyến DM CMtam giác DEM=tam giác DFM b)CM DM vuông góc EF c)biết DE=DF=13 È=10 tính DM d)gọi g trọng tâm của tam giác DEF tính GD
có ΔEDF cân ở D =>DE=DF; góc E =góc F
xét ΔDEM và ΔDFM có
DM là trung tuyến => EM=FM
góc E =góc F (cmt)
DE=DF (cmt)
=>ΔDEM = ΔDFM (cgc)
b)Có Δ DEF cân mà DM là trung tuyến
=> DM là đường cao (tc Δ cân )
=> DM⊥EF
c) EM=FM=EF/2=5
xét ΔDEM có DM ⊥ EF => góc EMD =90o
=>EM2+DM2=ED2 (đl pitago)
=>52+DM2=132 => DM=12
d) Ta có G là trọng tâm của ΔDEF
=>DG=2/3DM=> DG=2/3*12=8
Đúng 3
Bình luận (2)
a) Xét ΔDEM và ΔDFM có
DE=DF(ΔDEF cân tại D)
DM chung
EM=FM(M là trung điểm của EF)
Do đó: ΔDEM=ΔDFM(c-c-c)
Đúng 1
Bình luận (0)
b) Ta có: DE=DF(ΔDEF cân tại D)
nên D nằm trên đường trung trực của EF(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ME=MF(M là trung điểm của EF)
nên M nằm trên đường trung trực của EF(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra DM là đường trung trực của EF
hay DM\(\perp\)EF(Đpcm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tam giác DEF vuông tại có DE<DF.Gọi M là trung điểm EF. Biết DE=3cm, DF=4cm, FE=5cm. Tính DM.
Vì DM là trung tuyến ứng với cạnh huyền EF nên \(DM=\dfrac{1}{2}EF=\dfrac{5}{2}=2,5\left(cm\right)\)
Đúng 3
Bình luận (1)
Câu 1: Cho tam giác DEF vuông tại D có DE = 12cm, DF = 9cm, DM là đường trung tuyến (M thuộc EF). a) Tính EF, DM. b) Gọi N và K lần lượt là chân các đường vuông góc hạ từ M xuống DE và DF. Tứ giác DNMK là hình gì? Vì sao? c) Gọi H là điểm đối xứng với M qua N, O là trung điểm của MD. Chứng minh rằng ba điểm H, O, F thẳng hàng rồi.
a: ΔDEF vuông tại D
=>\(DE^2+DF^2+EF^2\)
=>\(EF^2=9^2+12^2=225\)
=>\(EF=\sqrt{225}=15\left(cm\right)\)
Ta có; ΔDEF vuông tại D
mà DM là đường trung tuyến
nên \(DM=\dfrac{EF}{2}=7,5\left(cm\right)\)
b: Xét tứ giác DNMK có
\(\widehat{DNM}=\widehat{DKM}=\widehat{KDN}=90^0\)
=>DNMK là hình chữ nhật
c: Xét ΔDEF có MN//DF
nên \(\dfrac{MN}{DF}=\dfrac{EM}{EF}\)
=>\(\dfrac{MN}{DF}=\dfrac{1}{2}\)
mà \(MN=\dfrac{1}{2}MH\)
nên MH=DF
Ta có: MN//DF
N\(\in\)MH
Do đó: MH//DF
Xét tứ giác DHMF có
MH//DF
MH=DF
Do đó: DHMF là hình bình hành
=>DM cắt HF tại trung điểm của mỗi đường
mà O là trung điểm của DM
nên O là trung điểm của HF
=>H,O,F thẳng hàng
Đúng 1
Bình luận (0)
cho tam giác DEF có DE =9cm , DF = 15 cm , EF = 21 cm . lấy M,N, thuộc DE , DF sao cho DM = 3cm , DN = 5cm
a, chứng minh MN //EF
b, Tính MN
c, kẻ trung tuyến DI của tam giác DEF . DI cắt MN tại K . Chứng minh K là trung điểm MN
Cho tam giác DEF vuông tại D, gọi M là trung điểm của EF. Qua M kẻ MP vuông góc với DF tại Q 1) Chứng minh tứ giác DPMQ là hình chữ nhật 2) Biết EF= 5cm. Tính độ dài DM 3) Gọi H là điểm đối xứng với M qua DE, Glaf điểm đối xứng với M qua DF. Chứng minh H đối xứng với G qua D
a/ Xét tứ giác DPMQ có
∠EDF=∠MQD=ˆMPD=90oEDF^=MQD^=MPD^=90o
=> Tứ giác DPMQ là hcn
b/ Để hcn DPMQ là hình vuông thì DM là tia pg ^EDF
c/ Có I đx M qua DE
=> DE là đường t/trực của IM
=> DI = DM (1)
=> t/g DIM cân tại D có DE là đường trung trực
=> DE đồng thời là đường pg
=> ˆIDE=ˆEDMIDE^=EDM^ (2)
CMTT : DM = DK (3) ; ˆKDF=ˆFDMKDF^=FDM^ (4)
Từ (2) ; (4)
=> ∠IDE+∠EDF+∠KDF=∠IDK=180oIDE^+EDF^+KDF^=IDK^=180o
=> I,D,K thẳng hàng
Từ (1) ; (3)=> ID = DK
Do đó D là trđ IK
=> I đx K qua D
Đúng 1
Bình luận (0)
Cho tam giác DEF cân tại D với đường trung tuyến DI.
Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.
I là trung điểm của EF nên IE = IF = EF/2 = 5cm.
Ta có : 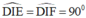 ⇒ ΔDIE vuông tại I
⇒ ΔDIE vuông tại I
Theo định lý Pitago trong tam giác vuông DIE ta có :
DE2 = DI2 + EI2 ⇒ DI2 = DE2 – EI2 = 132 – 52 = 144 ⇒ DI = 12 (cm).
Đúng 1
Bình luận (0)
Cho tam giác DEF có DE = 3cm , DF = 4cm, EF = 5CM. DI là đường trung tuyến ứng với xạnh EF
a) Chứng minh tam giăc DEF vuông.
b) Tính độ dài đoạn thẳng DI
c) Qua I kẻ IK vuông góc DF. Tính độ dài đoạn thẳng IK

a) Ta có: \(DE^2+DF^2=3^2+4^2=25\left(cm\right)\)
và \(EF^2=5^2=25\left(cm\right)\)
\(\Rightarrow DE^2+DF^2=EF^2\)
\(\Delta DEF\)có ba cạnh thỏa mãn định lý Py - ta - go nên \(\Delta DEF\) vuông
b) Vì DI là trung tuyến ứng với cạnh huyền của tam giác vuông \(DEF\)nên \(DI=\frac{1}{2}EF\)
\(\Rightarrow DI=\frac{1}{2}.5=2,5\left(cm\right)\)
c) Vì DI là trung tuyến ứng với cạnh huyền của tam giác vuông \(DEF\)nên \(DI=FI=EI\)
Lại có IK vuông góc DF
\(\Rightarrow\)IK là đường trung trực của đoạn thẳng DF
\(\Rightarrow IK=\frac{1}{2}DF=\frac{1}{2}.4=2\left(cm\right)\)
đề chẵn 2. cho tam giác DEF vuông tại D, có DE= 9 cm, DF =12 cm, DM là đường trung tuyến ứng với cạnh EF. vẽ MN song song DE, MP song song DF
a/ tính DM
b/ tứ giác DNMMP là hình gì, vì sao
c/ tìm điều kiện của tam giác DEF để tứ giác DNMP là hình vuông
bài này tương tự bài 1
a) EF = 15
=> DM = EM = FM = 7,5
b) MND + D = 180
MND + 90 = 180
=> MND = 90
D + MED = 180
90 + MED = 180
=> MED = 90
=> DNME là hình chữ nhật
c) y hệt như bài trước mik giải
Đúng 0
Bình luận (0)
Cho tam giác DEF vuông tại D, đường cao DH. Hãy tính lần lượt độ dài các đoạn EF,DH nếu biết:
a)DE=3cm; DF=4cm
b)DE=12cm;DF=9cm
c)DE=12cm;DF=5cm
a) \(EF=\sqrt{3^2+4^2}=5\)(cm)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{3\cdot4}{5}=\dfrac{12}{5}=2,4\left(cm\right)\)
b) \(EF=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cm\right)\)
c) \(EF=\sqrt{12^2+5^2}=13\left(cm\right)\)
\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\)
Đúng 1
Bình luận (0)




