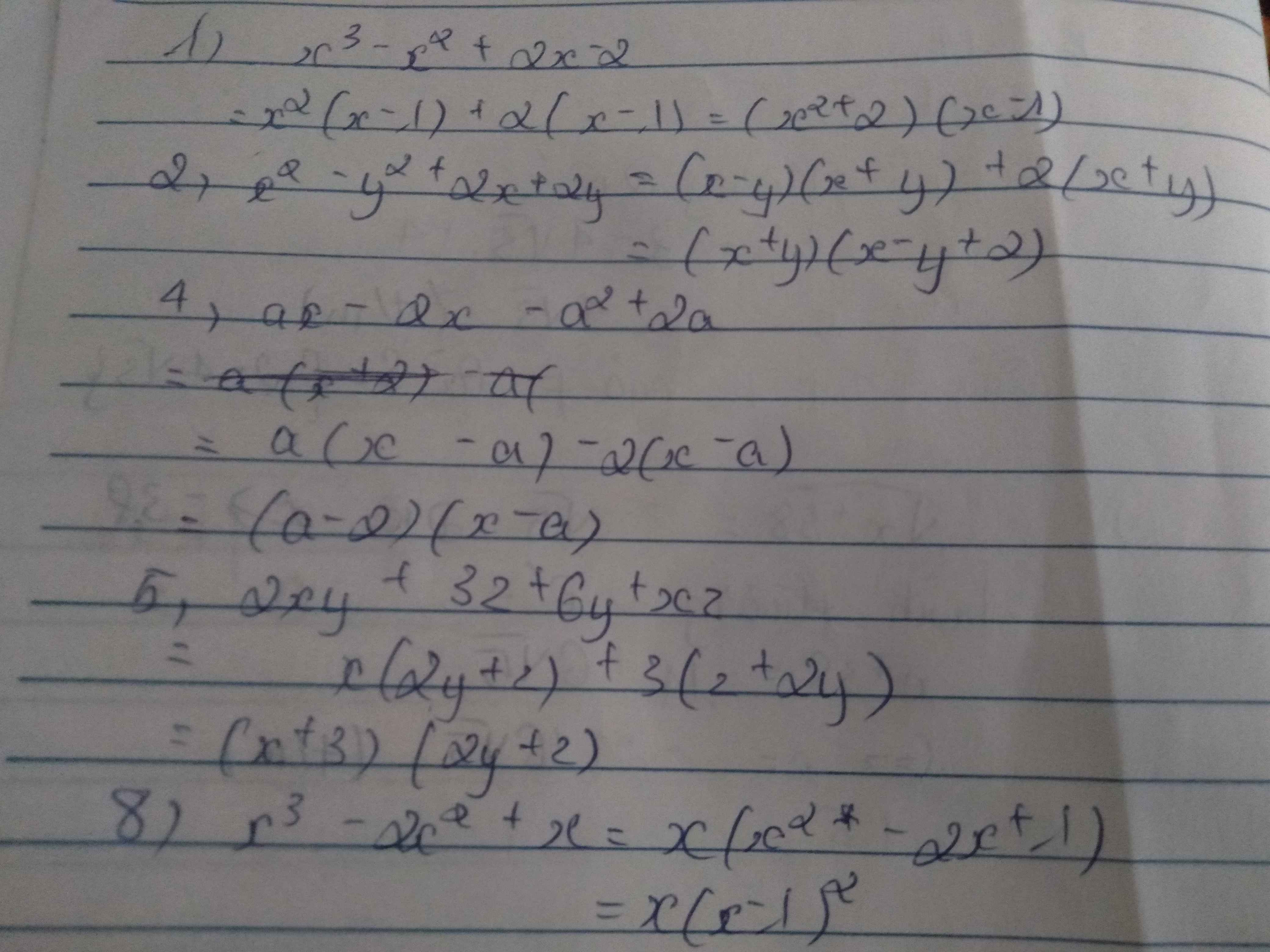2X\(\dfrac{4}{6}X3=\)
KS
Những câu hỏi liên quan
Bài 1: Thực hiện phép tính:
a) (2x4-x3 5x-6x2-1):(1-2x)
b)(x3-3x2 3x-2):(x2-x 1)
c) (2x3 5x2-2x 3):(2x2-x 1)
d)\(\dfrac{5x y^2}{x^2y}\) \(\dfrac{5y-x^2}{xy^2}\)
e)\(\dfrac{27-x^3}{5x 5}\):\(\dfrac{2x-6}{3x 3}\)
f)\(\dfrac{x 2}{4x 24}\).\(\dfrac...
Xem chi tiết
\(\dfrac{3}{4}+\dfrac{1}{6}x3+\dfrac{2}{5}:\dfrac{4}{15}\)
\(\dfrac{3}{4}+\dfrac{1}{6}\times3+\dfrac{2}{5}:\dfrac{4}{15}\)
\(=\dfrac{3}{4}+\dfrac{1}{2}+\dfrac{2}{5}\times\dfrac{15}{4}\)
\(=\dfrac{3}{4}+\dfrac{1}{2}+\dfrac{3}{2}\) \(=\dfrac{3+2+3}{4}=\dfrac{8}{4}=2\)
Đúng 1
Bình luận (1)
Gọi số đó là \(\overline{abcd}\) \(\left(a\ne0\right)\)
Ta có: \(\overline{abcd}+a+b+c+d=2020\)
\(\Leftrightarrow1000a+100b+10c+d+a+b+c+d=2020\)
\(\Leftrightarrow1001a+101b+11c+2d=2020\)
Đúng 0
Bình luận (1)
a) \(\dfrac{11}{13}-\left(\dfrac{5}{42}-x\right)=\left(\dfrac{15}{28}-\dfrac{11}{13}\right)\)
b) \(\left(\dfrac{7}{2}-2x\right)x3\dfrac{2}{5}+1\dfrac{4}{5}=7\dfrac{6}{5}\)
c) \(\left|2x-\dfrac{1}{3}\right|=\dfrac{5}{3}-2\)
d) (2x-1)3= -27
e) \(\dfrac{16}{2x}=1\)
a: =>5/42-x=11/13-15/28+11/13=421/364
=>x=-1193/1092
b: =>\(\dfrac{7}{2}-2x=7+\dfrac{6}{5}-3-\dfrac{2}{5}-1-\dfrac{4}{5}=3\)
=>2x=1/2
=>x=1/4
c: =>|2x-1/3|=-1/3(vô lý)
d: =>2x-1=-3
=>2x=-2
hay x=-1
e: =>2x=16
hay x=8
Đúng 0
Bình luận (0)
1. Tìm \(m\in\left[-10;10\right]\) để pt \(\left(x^2-2x+m\right)^2-2x^2+3x-m=0\) có 4 ng pb
2. Cho biết x1,x2 là nghiệm của pt \(x^2-x+a=0\) và x3,x4 là nghiệm của pt \(x^2-4x+b=0\) . Biết rằng \(\dfrac{x2}{x1}=\dfrac{x3}{x2}=\dfrac{x4}{x3}\), b >0 . Tìm a
1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
Đúng 3
Bình luận (1)
Bài 5: Giải các phương trình sau:a. (3x - 1)2 - (x + 3)2 0b. x3 dfrac{x}{49}c. x2 - 7x + 12 0d. 4x2 - 3x -1 0e. x3 - 2x - 4 0f. x3 + 8x2 + 17x +10 0g. x3 + 3x2 + 6x + 4 0h. x3 - 11x2 + 30x 0
Đọc tiếp
Bài 5: Giải các phương trình sau:
a. (3x - 1)2 - (x + 3)2 = 0
b. x3 = \(\dfrac{x}{49}\)
c. x2 - 7x + 12 = 0
d. 4x2 - 3x -1 = 0
e. x3 - 2x - 4 = 0
f. x3 + 8x2 + 17x +10 = 0
g. x3 + 3x2 + 6x + 4 = 0
h. x3 - 11x2 + 30x = 0
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
Đúng 3
Bình luận (0)
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
Đúng 2
Bình luận (0)
*Cách khác:
a) Ta có: \(\left(3x-1\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(3x-1\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=-x-3\\3x-1=x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-2\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{1}{2};2\right\}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
1) (\(\dfrac{1}{2}\)x + 3)*(x2- 4x- 6)
2) (6x2 -9x +15)*(\(\dfrac{2}{3}\)x+1)
3) (3x2 -x+5)*(x3+5x-1)
4) (x-1)*(x+1)*(x-2)
5) D=(x-7)*(x+5)-(x-4)*(x+3)
6) E= 4x*(x2-x-1)-(x+3)*(x2-2)
7) F= 5x*(x-3)*(x-1)-4x*(x2-2x)
1) \(\left(\dfrac{1}{2}x+3\right)\left(x^2-4x-6\right)\)
\(=\dfrac{1}{2}x^3-2x^2-3x+3x^2-12x-18\)
\(=\dfrac{1}{2}x^3+x^2-15x-18\)
2) \(\left(6x^2-9x+15\right)\left(\dfrac{2}{3}x+1\right)\)
\(=4x^3+6x^2-6x^2-9x+10x+15\)
\(=4x^3+x+15\)
3) Ta có: \(\left(3x^2-x+5\right)\left(x^3+5x-1\right)\)
\(=3x^5+15x^2-3x^2-x^4-5x^2+x+5x^3+25x-5\)
\(=3x^5-x^4+5x^3+10x^2+26x-5\)
4) Ta có: \(\left(x-1\right)\left(x+1\right)\left(x-2\right)\)
\(=\left(x^2-1\right)\left(x-2\right)\)
\(=x^3-2x^2-x+2\)
Đúng 2
Bình luận (0)
1) x3-x2+2x-2 4) ax-2x-a2+2a 7) x2-6xy-25z2+9y2
2) x2-y2+2x+2y 5) 2xy +3z+6y+xz 8) x3-2x2+x
3) x2/4+2xy+4y2-25 6) x2y2+yz+y3+zx2 9) x4+4
Bài 1: Giải phương trình:
a) 2x2-6=0
b)x3-5x2+6x=0
c) \(\dfrac{3}{x-1}+\dfrac{2}{x^{2^{ }}+x+1}=\dfrac{3x^2}{x^3-1}\)
Bài 2: Tìm MIN của
A=\(\dfrac{2}{-x^2-2x-2}\)
Bài 2:
\(A=\dfrac{2}{-x^2-2x-2}=\dfrac{-2\left(-x^2-2x-2\right)-2x^2-4x-2}{-x^2-2x-2}\) \(=-2+\dfrac{2\left(x+1\right)^2}{-x^2-2x-2}\ge-2\)
Dấu bằng xảy ra \(\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
Vậy \(A_{Min}=-2\) khi \(x=-1\)
Đúng 2
Bình luận (0)
Bài 1:
a) Ta có: \(2x^2-6=0\)
\(\Leftrightarrow2x^2=6\)
\(\Leftrightarrow x^2=3\)
hay \(x\in\left\{\sqrt{3};-\sqrt{3}\right\}\)
Vậy: \(S=\left\{\sqrt{3};-\sqrt{3}\right\}\)
Đúng 0
Bình luận (0)
Bài 1. Làm tính nhân:a) 3x2 (2 - 5xy) b) -dfrac{2}{3} xy (xy2 - x3 + 4) c) ( x - 7 y )( xy + 1)Bài 2. Rút gọn các biểu thức sau:a) 5x(4x2 - 2x +1) - 2x(10x2 - 5x - 2)b) 3x( x - 2) - 5x(1- x) - 8(x2 - 3)d) (x3 - 2x)(x2 +1)
Đọc tiếp
Bài 1. Làm tính nhân:
a) 3x2 (2 - 5xy)
b) -\(\dfrac{2}{3}\) xy (xy2 - x3 + 4)
c) ( x - 7 y )( xy + 1)
Bài 2. Rút gọn các biểu thức sau:
a) 5x(4x2 - 2x +1) - 2x(10x2 - 5x - 2)
b) 3x( x - 2) - 5x(1- x) - 8(x2 - 3)
d) (x3 - 2x)(x2 +1)
Bài 1:
\(a,6x^2-15x^3y\\ b,=-\dfrac{2}{3}x^2y^3+\dfrac{2}{3}x^4y-\dfrac{8}{3}xy\)
Bài 2:
\(a,=20x^3-10x^2+5x-20x^3+10x^2+4x=9x\\ b,=3x^2-6x-5x+5x^2-8x^2+24=24-11x\\ c,=x^5+x^3-2x^3-2x=x^5-x^3-2x\)
Đúng 1
Bình luận (0)
câu d của bài 2 là của bài 1 nha mình để nhầm chỗ huhu
Đúng 0
Bình luận (0)