\(\Leftrightarrow\sqrt{-x^2-2x+15}-x^2-2x+15\le a+15\)

Đặt \(\sqrt{-x^2-2x+15}=t\ge0\)

Đồng thời ta có: \(\sqrt{-x^2-2x+15}=\sqrt{\left(x+5\right)\left(3-x\right)}\le\dfrac{1}{2}\left(x+5+3-x\right)=4\)

\(\Rightarrow0\le t\le4\)

BPT trở thành: \(t^2+t\le a+15\Leftrightarrow t^2+t-15\le a\) ; \(\forall t\in\left[0;4\right]\)

\(\Leftrightarrow a\ge\max\limits_{t\in\left[0;4\right]}\left(t^2+t-15\right)\)

Xét hàm \(f\left(t\right)=t^2+t-15\) trên \(\left[0;4\right]\)

\(-\dfrac{b}{2a}=-\dfrac{1}{2}\notin\left[0;4\right]\) ; \(f\left(0\right)=-15\) ; \(f\left(4\right)=5\)

\(\Rightarrow f\left(t\right)_{max}=4\Rightarrow a\ge4\)

Bước 1: Mở trang Geoebra

Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô

Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).

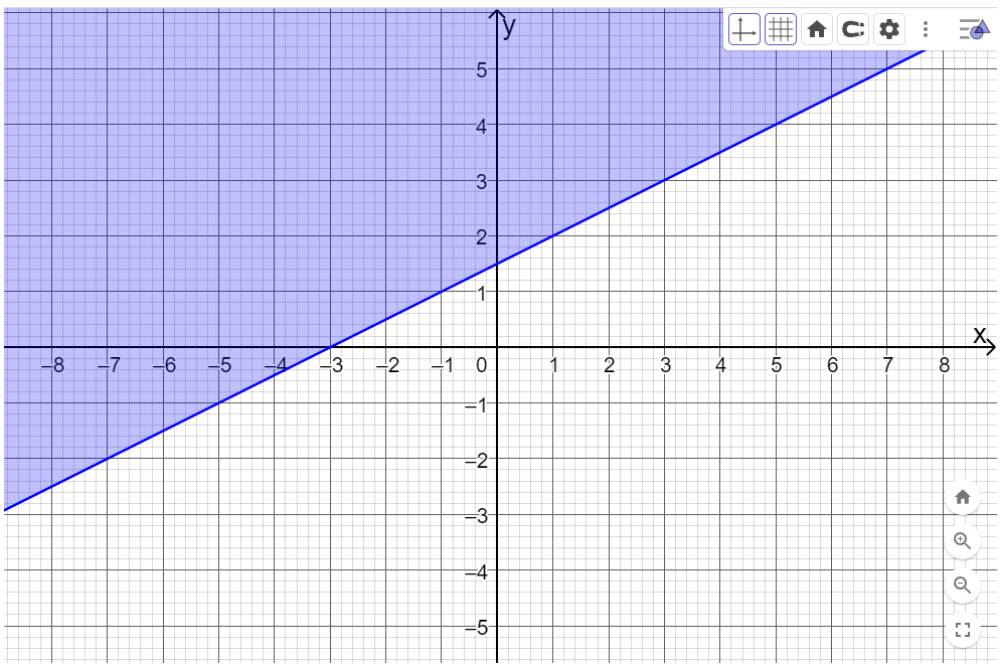
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:

x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.

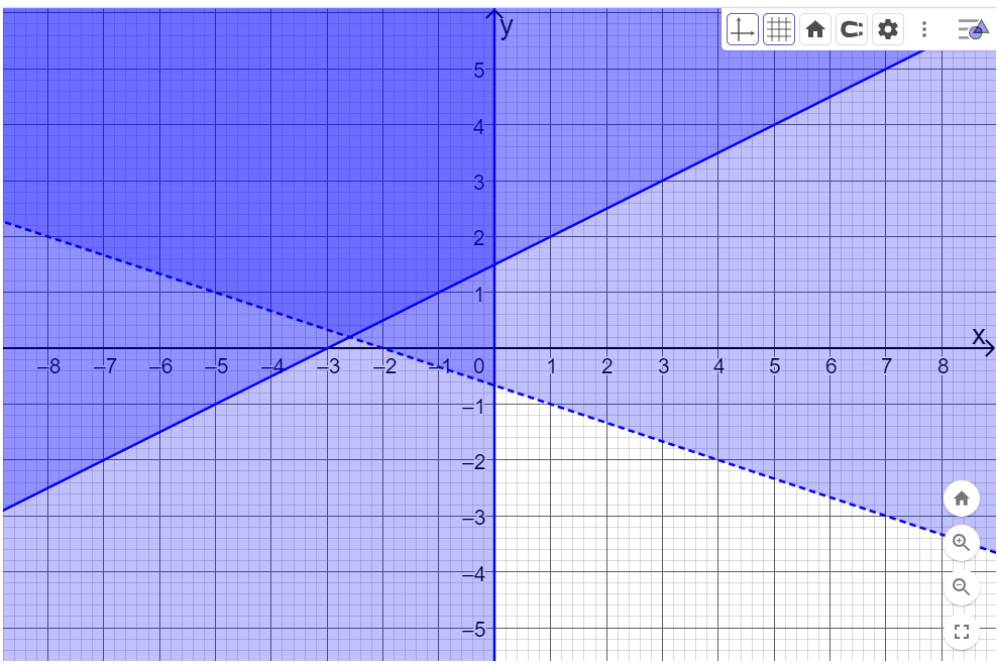
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y =  - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.

ĐKXĐ: \(x>4\)

\(\dfrac{x-2}{\sqrt{x-4}}\le\dfrac{4}{\sqrt{x-4}}\Rightarrow x-2\le4\)

\(\Rightarrow x\le6\Rightarrow4< x\le6\)

\(\Rightarrow x=\left\{5;6\right\}\Rightarrow5+6=11\)

x=\(\left\{{}\begin{matrix}x=3\\x=-3\\x=-2\end{matrix}\right.\)

\(\Rightarrow\) (-\(\infty\); -3] \(\cup\) { 3 }

\(\left(16-x^2\right)\sqrt{x-3}\le0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-3\ge0\\16-x^2\le0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge3\\x\in(-\infty;-4]\cup[4;+\infty)\end{matrix}\right.\)

\(\Leftrightarrow\left\{3\right\}\cup[4;+\infty)\)

TXĐ: \(x>-4\)

Khi đó BPT tương đương:

\(x^2+2x>3\Leftrightarrow x^2+2x-3>0\)

\(\Rightarrow\left[{}\begin{matrix}x>1\\x< -3\end{matrix}\right.\)

Vậy tập nghiệm của BPT là: \(\left[{}\begin{matrix}x>1\\-3< x< -3\end{matrix}\right.\)