Tam giác ABC vuông tại A áp dụng đính lý cạnh góc vuông và hình chiếu ta có::

\(AB^2=BC\cdot HB=BC\cdot\left(BC-HC\right)\)

\(\Rightarrow20^2=BC^2-BC\cdot9\)

\(\Rightarrow BC^2-9BC-400=0\)

\(\Rightarrow BC^2+16BC-25BC-400=0\)

\(\Rightarrow BC\left(BC+16\right)-25\left(BC+16\right)=0\)

\(\Rightarrow\left(BC+16\right)\left(BC-25\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}BC+16=0\\BC-25=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}BC=-16\left(ktm\right)\\BC=25\left(tm\right)\end{matrix}\right.\)

Áp dụng hệ thức đường cao và hình chiếu ta có:

\(AH^2=HC\cdot HB\Rightarrow AH=\sqrt{HC\cdot\left(BC-HC\right)}\)

\(\Rightarrow AH=\sqrt{9\cdot\left(25-9\right)}=12\left(cm\right)\)

Diện tích của tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot AH=\dfrac{1}{2}\cdot25\cdot12=150\left(cm^2\right)\)

a: BC=15cm

AM=7,5cm

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A

Ta có: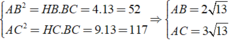

Vậy S A B C   =   1 2 A B . A C   =   1 2 . 2 13   . 3 13 =   39 c m 2

Chọn đáp án A.

Đáp án A.

Giả sử cạnh góc vuông có độ dài bằng X x 0 < x < a .

Suy ra độ dài cạnh huyền là a - x .

Độ dài cạnh góc vuông còn lại là a - x 2 - x 2 = a 2 - 2 a x .

Diện tích tam giác vuông đó được tính bằng công thức S = 1 2 x . a 2 - 2 a x .

S = 1 2 a . a x . a x . a 2 - 2 a x ≤ 1 2 a . a x + a x + a 2 - 2 a x 3 3 = 1 2 a . a 6 27 = a 2 3 18 .

Dấu bằng xảy ra khi a x = a 2 - 2 a x ⇔ x = a 3 .