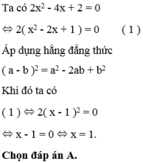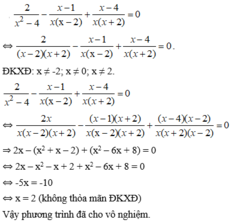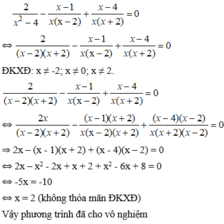2x2-4x+2=0
HT
Những câu hỏi liên quan
Giải các pt sau
a) 3x2 + 4x = 0
b) -2x2 - 8 = 0
c) 2x2 -7x2 + 5 = 0
d) x^2 - 8x - 48 = 0
cho mik hỏi rằng là 3x2 + 4x = 0 hay 3x2 + 4x = 0
Đúng 0
Bình luận (1)
ông ơi mấy bài này bấm máy tính là ra mà ông
Đúng 0
Bình luận (0)
a) \(3x^2+4x=0\Leftrightarrow\left(3x+4\right)x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\3x+4=0\Leftrightarrow x=-\dfrac{4}{3}\end{matrix}\right.\)
➤\(x\in\left\{0;-\dfrac{4}{3}\right\}\)
b) \(-2x^2-8=0\Leftrightarrow-2x^2+\left(-2\right)\cdot4=0\)
\(\Leftrightarrow\left(x^2+4\right)\cdot\left(-2\right)=0\\ \Leftrightarrow x^2+4=0\\\Rightarrow x^2=\varnothing\Leftrightarrow x=\varnothing \)
vì với mọi x, ta luôn đúng với: \(x^2\ge0\Leftrightarrow x^2+4\ge4>0\)
➤\(x=\varnothing\)
c)\(2x^2-7x^2+5=0\)
+) \(a+b+c=2+\left(-7\right)+5=7-7=0\)
Do đó, phương trình có 2 nghiệm sau:
\(x=1\) và \(x=\dfrac{5}{2}=2,5\)
➤\(x\in\left\{1;2,5\right\}\)
d) \(x^2-8x-48=0\)
+)\(\Delta=\left(-8\right)^2-4\cdot1\cdot\left(-48\right)=64+192=266>0\)
\(\Leftrightarrow\sqrt{\Delta}=\sqrt{266}\)
➢Do đó, ta có: \(\left[{}\begin{matrix}x=\dfrac{\sqrt{266}-\left(-8\right)}{2\cdot2}=\dfrac{\sqrt{266}+8}{4}\\x=\dfrac{-\sqrt{266}-\left(-8\right)}{2\cdot2}=\dfrac{8-\sqrt{266}}{4}\end{matrix}\right.\)
➤ \(x\in\left\{\dfrac{8+\sqrt{266}}{4};\dfrac{8-\sqrt{266}}{4}\right\}\)
Đúng 1
Bình luận (0)
2x2-4x+2=0
\(2x^2-4x+2=0\\ \Leftrightarrow2\left(x^2-2x+1\right)=0\\ \Leftrightarrow2\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)^2=0\\ \Leftrightarrow x-1=0\\ \Leftrightarrow x=1\)
Đúng 1
Bình luận (0)
\(2x^2-4x+2=0\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left\{{}x=1}\)
Đúng 1
Bình luận (0)
a. (x – 1)(5x + 3) = (3x – 8)(x – 1)
b. 3x(25x + 15) – 35(5x + 3) = 0
c. (2 – 3x)(x + 11) = (3x – 2)(2 – 5x)
d. (2x2 + 1)(4x – 3) = (2x2 + 1)(x – 12)
e. (2x – 1)2 + (2 – x)(2x – 1) = 0
f. (x + 2)(3 – 4x) = x2 + 4x + 4
\(a,\left(x-1\right)\left(5x+3\right)=\left(3x-8\right)\left(x-1\right)\)
\(\left(x-1\right)\left(5x+3-3x+8\right)=0\)
\(\left(x-1\right)\left(2x+11\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\2x+11=0\end{cases}\Rightarrow\orbr{\begin{cases}x=1\\2x=-11\end{cases}\Rightarrow}\orbr{\begin{cases}x=1\\x=-\frac{11}{2}\end{cases}}}\)
\(b,3x\left(25x+15\right)-35\left(5x+3\right)=0\)
\(15x\left(5x+3\right)-35\left(5x+3\right)=0\)
\(\left(5x+3\right).5\left(3x-7\right)=0\)
\(\Rightarrow\orbr{\begin{cases}5x+3=0\\5\left(3x-7\right)=0\end{cases}\Rightarrow\orbr{\begin{cases}5x=-3\\3x-7=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=-\frac{3}{5}\\3x=7\end{cases}\Rightarrow}\orbr{\begin{cases}x=-\frac{3}{5}\\x=\frac{7}{3}\end{cases}}}\)
\(c,\left(2-3x\right)\left(x+11\right)=\left(3x-2\right)\left(2-5x\right)\)
\(\left(3x-2\right)\left(2-5x\right)+\left(3x-2\right)\left(x+11\right)=0\)
\(\left(3x-2\right)\left(2-5x+x+11\right)=0\)
\(\left(3x-2\right)\left(13-4x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x-2=0\\13-4x=0\end{cases}\Rightarrow\orbr{\begin{cases}3x=2\\4x=13\end{cases}\Rightarrow}\orbr{\begin{cases}x=\frac{2}{3}\\x=\frac{13}{4}\end{cases}}}\)
còn đâu tự lm lười :_#
Xem thêm câu trả lời
Giá trị của x thỏa mãn 2 x 2 - 4 x + 2 = 0 là ?
A. x = 1.
B. x = - 1.
C. x = 2.
D. x = - 2.
Giải các phương trình sau:
2
x
2
-
4
-
x
-
1
x
(
x
-
2
)
+
x
-
4
x
(
x
+
2
)...
Đọc tiếp
Giải các phương trình sau: 2 x 2 - 4 - x - 1 x ( x - 2 ) + x - 4 x ( x + 2 ) = 0
Giải các phương trình sau:
2
x
2
-
4
-
x
-
1
x
(
x
-
2
)
+
x
-
4
x
(
x
+
2
)...
Đọc tiếp
Giải các phương trình sau: 2 x 2 - 4 - x - 1 x ( x - 2 ) + x - 4 x ( x + 2 ) = 0
1) Phân tích đa thức thành nhân tử
a) 2x4-4x3+2x2
b) 2x2-2xy+5x-5y
2) Tìm x, biết:
a) 4x(x-3)-x+3=0
b)(2x-3)2-(x+1)2=0
1.
a) \(2x^4-4x^3+2x^2\)
\(=2x^2\left(x^2-2x+1\right)\)
\(=2x^2\left(x-1\right)^2\)
b) \(2x^2-2xy+5x-5y\)
\(=\left(2x^2-2xy\right)+\left(5x-5y\right)\)
\(=2x\left(x-y\right)+5\left(x-y\right)\)
\(=\left(x-y\right)\cdot\left(2x+5\right)\)
Đúng 1
Bình luận (0)
2 .
a,
\(4x\left(x-3\right)-x+3=0\)
⇒\(4x\left(x-3\right)-\left(x-3\right)=0\)
⇒\(\left(x-3\right)\left(4x-1\right)=0\)
⇒\(\left[{}\begin{matrix}x-3=0\\4x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=3\\4x=1\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=3\\x=\dfrac{1}{4}\end{matrix}\right.\)
vậy \(x\in\left\{3;\dfrac{1}{4}\right\}\)
b,
\(\)\(\left(2x-3\right)^2-\left(x+1\right)^2=0\)
⇒\(\left(2x-3-x-1\right)\left(2x-3+x+1\right)\) = 0
⇒\(\left(x-4\right)\left(3x-2\right)=0\)
⇔\(\left[{}\begin{matrix}x-4=0\\3x-2=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=4\\3x=2\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=4\\x=\dfrac{2}{3}\end{matrix}\right.\)
vậy \(x\in\left\{4;\dfrac{2}{3}\right\}\)
Đúng 1
Bình luận (0)
Bài 1: Tìm x
a) (x-4)2-(x-3)(x+3)=5
b) 2x2+4x+2-2y2=0
a: \(\left(x-4\right)^2-\left(x-3\right)\left(x+3\right)=5\)
\(\Leftrightarrow x^2-8x+16-x^2+9=5\)
\(\Leftrightarrow-8x=-20\)
hay \(x=\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
Cho biểu thức :
P
x
2
-
2
x
2
x
2
+
8
-
2
x
2
8...
Đọc tiếp
Cho biểu thức : P = x 2 - 2 x 2 x 2 + 8 - 2 x 2 8 - 4 x + 2 x 2 - x 3 1 - 1 x - 2 x 2 x ≠ 0 , x ≠ 2
a) Rút gọn biểu thức P
b) Tính giá trị biểu thức P với x = 1/2
a) Ta có: 2x2 + 8 = 2(x2 + 4).
8 – 4x + 2x2 – x3
= (8 – x3) - ( 4x - 2x2)
= (2 – x).(4 + 2x + x2) - 2x.(2 - x)
= (2 – x).(4 + 2x + x2 – 2x)
= (2 - x). (4 + x2 )
* Do đó:
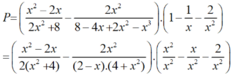
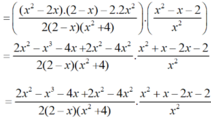
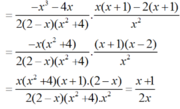
b) Tại x = 1 2 hàm số đã cho xác định nên thay x = 1 2 vào biểu thức rút gọn của P ta được:
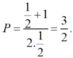
Đúng 0
Bình luận (0)