Cho 3 so duong a,b,c thoa man ab+bc+ac=3abc.Chung minh(a/a2+bc)+(b/b2+ac)+(c/c2+ba)<=3/2
H24
Những câu hỏi liên quan
cho ba so a,b,c khac 0 thoa man ab+bc +ac = 0 .tinh B=bc/a2 + ca/b2 + ab/c2
\(ab+bc+ca=0\)
=> \(\frac{ab+bc+ca}{abc}=0\)
=> \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
Đặt: \(\frac{1}{a}=x;\)\(\frac{1}{b}=y;\)\(\frac{1}{c}=z\)
Ta có: \(x+y+z=0\)
=> \(x^3+y^3+z^3=3xyz\) (tự c/m, ko c/m đc ib)
hay \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)
\(B=\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}=\frac{abc}{a^3}+\frac{abc}{b^3}+\frac{abc}{c^3}=abc.\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)\)
\(=abc.\frac{3}{abc}=3\)
Đúng 1
Bình luận (0)
Phân tích thành nhân tử :
a). a(b2 + c2 + bc) + b(c2 + a2 + ac) + c(a2 + b2 + ab);
b). (a + b + c) (ab + bc + ca) - abc
c*). a(a + 2b)3 - b(2a + b)3.
c: Ta có: \(a\left(a+2b\right)^3-b\left(2a+b\right)^3\)
\(=a^4+6a^3b+12a^2b^2+8ab^3-8a^3b-12a^2b^2-6ab^3-b^4\)
\(=a^4-2a^3b+2ab^3-b^4\)
\(=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)-2ab\left(a^2-b^2\right)\)
\(=\left(a-b\right)^3\cdot\left(a+b\right)\)
Đúng 1
Bình luận (0)
Cho a2+b2 +c2 -ab-ac-bc=0
Chứng minh a=b=c
\(a^2+b^2+c^2-ab-ac-bc=0\\\Leftrightarrow 2a^2+2b^2+2c^2-2ab-2ac-2bc=0\\\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(a^2-2ac+c^2)=0\\\Leftrightarrow (a-b)^2+(b-c)^2+(a-c)^2=0\)
Ta thấy: \(\left(a-b\right)^2\ge0\forall a;b\)
\(\left(b-c\right)^2\ge0\forall b;c\)
\(\left(a-c\right)^2\ge0\forall a;c\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\ge0\forall a;b;c\)
Mặt khác: \(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
nên: \(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=b\\b=c\\a=c\end{matrix}\right.\)
\(\Leftrightarrow a=b=c\left(dpcm\right)\)
#\(Toru\)
Đúng 0
Bình luận (0)
Cho biết [a+b+c]2 \(=\) a2 + b2 + c2.CMR :
bc/a2 + ac/a2 +ab/c2 \(=\) 3
\(\left(a+b+c\right)^2=a^2+b^2+c^2\Leftrightarrow ab+bc+ca=0\)
\(\Rightarrow a^3b^3+b^3c^3+c^3a^3=3a^2b^2c^2\)
Ta có:
\(\dfrac{bc}{a^2}+\dfrac{ac}{b^2}+\dfrac{ab}{c^2}=\dfrac{a^3b^3+b^3c^3+c^3a^3}{a^2b^2c^2}=\dfrac{3a^2b^2c^2}{a^2b^2c^2}=3\)
Đúng 1
Bình luận (0)
1.Cho 3 số dương a,b,c. Chứng minh rằng:
\(\dfrac{19b^3-a^3}{ab+5b^2}+\dfrac{19c^3-b^3}{bc+5c^2}+\dfrac{19a^3-c^3}{ac+5a^2}\)≤ 3(a+b+c)
2.cho a,b,c dương thỏa man: a2+b2+c2=1
Tìm giá trị nhỏ nhất của biểu thức: P=\(\dfrac{bc}{a}+\dfrac{ac}{b}+\dfrac{ab}{c}\)
Cho a,b,c không âm. Chứng minh rằng :
a) a2 + b2 + c2 + 2abc + 2 > hoặc=ab +bc +ca +a+b+c
b)a2 + b2 +c2 +abc +4 > hoặc = 2(ab+bc+ca)
c) 3(a2 + b2 + c2) + abc +4 > hoặc =4 (ab+bc+ca)
d) 3(a2 + b2 + c2) + abc +80 > 4(ab+bc+ca) + 8(a+b+c)
Ngu kkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
Cho a, b,c là độ dài ba cạnh tam giác. Chứng minh rằng: a/(a2 + bc) + 1/(b2+ ac) + s/(c2+ab) <= (a+b+c)/2abc
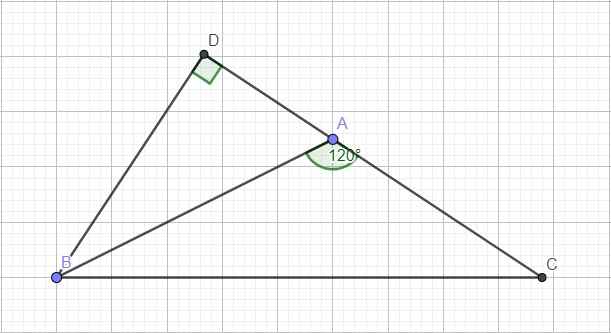
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)
cho a,b,c la ba so duong thoa man a+b+c=1 CMR:c+ab/a+b + a+bc/b+c + b+ac/a+c \(\ge\) 2
Áp dụng BĐT AM-GM ta có:
\(VT=\dfrac{c+ab}{a+b}+\dfrac{a+bc}{b+c}+\dfrac{b+ac}{a+c}\)
\(=\dfrac{c\left(a+b+c\right)+ab}{a+b}+\dfrac{a\left(a+b+c\right)+bc}{b+c}+\dfrac{b\left(a+b+c\right)+ac}{a+c}\)
\(=\dfrac{ac+bc+c^2+ab}{a+b}+\dfrac{a^2+ab+ac+bc}{b+c}+\dfrac{ab+b^2+bc+ac}{a+c}\)
\(=\dfrac{\left(b+c\right)\left(c+a\right)}{a+b}+\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}\)
\(\ge2\left(a+b+c\right)=2\left(a+b+c=1\right)\)
Khi \(a=b=c=\dfrac{1}{3}\)
Đúng 0
Bình luận (1)