a: Xét (O) có 

ΔABC nội tiếp đường tròn

AB là đường kính

Do đó: ΔABC vuông tại C

made

felt

began

falled

told

ate

drove

forgot

had

mờ quá mình ko đọc đc

Lời giải:

Các tập con của $A$ là:

$\varnothing$

\(\left\{1\right\}; \left\{23\right\}; \left\{456\right\}\)

\(\left\{1;23\right\}; \left\{1; 456\right\}; \left\{23; 456\right\}\)

\(\left\{1;23;456\right\}\)

a: Ta có: \(\widehat{DAH}+\widehat{DAB}=180^0\)

\(\widehat{CBK}+\widehat{CBA}=180^0\)

mà \(\widehat{DAB}=\widehat{CBA}\)

nên \(\widehat{DAH}=\widehat{CBK}\)

Xét ΔDAH vuông tại H và ΔCBK vuông tại K có 

DA=CB

\(\widehat{DAH}=\widehat{CBK}\)

Do đó: ΔDAH=ΔCBK

Suy ra: AH=BK

b: Xét tứ giác HKCD có 

HK//CD

HD//KC

Do đó: HKCD là hình bình hành

Suy ra: HK=CD

mà CD=10cm

nên HK=10cm

\(\Leftrightarrow AH=BK=\dfrac{HK-AB}{2}=\dfrac{10-6}{2}=2cm\)

a: Ta có: M và E đối xứng nhau qua AB

nên AB là đường trung trực của ME

Suy ra: AM=AE(1)

Ta có: M và F đối xứng nhau qua AC

nên AC là đường trung trực của MF

Suy ra: AM=AF(2)

Từ (1) và (2) suy ra AE=AF

b: Xét ΔAME có AM=AE

nên ΔAME cân tại A

mà AB là đường trung trực ứng với cạnh đáy ME

nên AB là tia phân giác của \(\widehat{MAE}\)

Xét ΔAMF có AM=AF

nên ΔAMF cân tại A

mà AC là đường trung trực ứng với cạnh đáy MF

nên AC là tia phân giác của \(\widehat{MAF}\)

Ta có: \(\widehat{EAF}=\widehat{FAM}+\widehat{EAM}\)

\(=2\cdot\left(\widehat{BAM}+\widehat{CAM}\right)\)

\(=2\cdot90^0=180^0\)

Do đó: E,A,F thẳng hàng

mà AE=AF

nên A là trung điểm của EF

Ta có: ΔABC cân tại A

mà AH là đường phân giác ứng với cạnh BC

nên AH là đường trung trực ứng với cạnh BC

Ta có: AE+EB=AB

AF+FC=AC

mà AE=AF

và AB=AC

nên EB=FC

Xét ΔEBH và ΔFCH có

EB=FC

\(\widehat{B}=\widehat{C}\)

HB=HC

Do đó: ΔEBH=ΔFCH

Suy ra: HE=HF

Ta có: AE=AF

nên A nằm trên đường trung trực của EF(1)

ta có: HE=HF

nên H nằm trên đường trung trực của EF(2)

Từ (1) và (2) suy ra AH là đường trung trực của FE

hay E và F đối xứng nhau qua AH

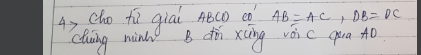
Ta có: DB=DC
nên D nằm trên đường trung trực của BC(1)

Ta có: AB=AC

nên A nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra AD là đường trung trực của BC

hay B và C đối xứng nhau qua AD