Cho tam giác ABC có 90𝑜 < 𝐵̂ < 135𝑜 , 𝐶̂ < 45𝑜 . Kẻ AD vuông góc với BC. Chứng minh 𝐵𝐷 < 𝐴𝐷 < 𝐶𝐷.
NT
Những câu hỏi liên quan
Cho hình thang 𝐴𝐵𝐶𝐷 (𝐴𝐷//𝐵𝐶) có đáy lớn 𝐵𝐶 𝐴𝐵 + 𝐶𝐷. Đường phân giác trong 𝐴̂, 𝐵̂ cắt nhau tại 𝐸; đường phân giác trong 𝐶̂, 𝐷̂ cắt nhau ở 𝐹. Đường phân giác ngoài 𝐴̂, 𝐵̂ cắt nhau ở 𝐼; đường phân giác ngoài của 𝐶̂, 𝐷̂ cắt nhau ở 𝐽. Đường thẳng 𝐴𝐸, 𝐴𝐼, 𝐶𝐽 cắt đường thẳng 𝐵𝐶 ở 𝐾, 𝑀, 𝑁. Gọi 𝐻, 𝐺 là trung điểm của 𝐴𝐵, 𝐶𝐷.a) Chứng minh rằng ∆𝐴𝐵𝐾 cân và 𝐸 là trung điểm 𝐴𝐾.b) Chứng minh rằng 𝐷𝐹 ⊥ 𝐶𝐹 và 𝐷, 𝐹, 𝐾 thẳng hàng.c) Chứng minh rằng 𝐼 là trung điểm 𝐴𝑀, 𝐽 là trung điểm...
Đọc tiếp
Cho hình thang 𝐴𝐵𝐶𝐷 (𝐴𝐷//𝐵𝐶) có đáy lớn 𝐵𝐶 = 𝐴𝐵 + 𝐶𝐷.
Đường phân giác trong 𝐴̂, 𝐵̂ cắt nhau tại 𝐸; đường phân giác trong 𝐶̂, 𝐷̂ cắt nhau ở 𝐹. Đường phân giác ngoài 𝐴̂, 𝐵̂ cắt nhau ở 𝐼; đường phân giác ngoài của 𝐶̂, 𝐷̂ cắt nhau ở 𝐽. Đường thẳng 𝐴𝐸, 𝐴𝐼, 𝐶𝐽 cắt đường thẳng 𝐵𝐶 ở 𝐾, 𝑀, 𝑁. Gọi 𝐻, 𝐺 là trung điểm của 𝐴𝐵, 𝐶𝐷.
a) Chứng minh rằng ∆𝐴𝐵𝐾 cân và 𝐸 là trung điểm 𝐴𝐾.
b) Chứng minh rằng 𝐷𝐹 ⊥ 𝐶𝐹 và 𝐷, 𝐹, 𝐾 thẳng hàng.
c) Chứng minh rằng 𝐼 là trung điểm 𝐴𝑀, 𝐽 là trung điểm 𝐷𝑁.
d) Chứng minh rằng 𝐼, 𝐺, 𝐸, 𝐹, 𝐻, 𝐽 thẳng hàng.
Cho tam giác ABC có 𝐴𝐶 ̂𝐷là góc ngoài tại đỉnh C và: 𝐴̂ = 𝐶̂ - 100; 𝐵̂ = 𝐶̂ + 100. Tính các góc của tam giác ABC và 𝐴𝐶𝐷 ̂.
Cho tam giác ABC vuông tại A, có 𝐵̂ = 60° và AB = 5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E. a) Tính số đo góc C b) Chứng minh: ABD = EBD.
Câu 6. Cho ∆ABC và ∆MNP có AB MN, BC NP, hai tam giác bằng nhau theo trường hợpcạnh – góc – cạnh nếu:A. 𝐵̂ 𝐶̂ B. 𝐵̂ 𝑀̂ C. 𝐵̂ 𝑃̂ D. 𝐵̂ 𝑁̂Câu 7. Cho ∆ABC ∆MNP biết góc A 50°, góc B 70°. Khi đó độ lớn góc P là:A. 60° B. 70° C. 50° D. Một kết quả khácCâu 8. Cho ∆ABC cân tại A có góc A 40°, khi đó số đo góc B là:A. 140° B. 40° C. 70° D. 180°Câu 9. Cho tam giác ABC đều cạnh 6cm, vẽ AH vuông góc BC tại H. Khi đó độ dài AH là:A. 6cm B. 3cm C. 27cm D. 3√3 cmCâu 10. Cho tam giác MNP có MK vuông...
Đọc tiếp
Câu 6. Cho ∆ABC và ∆MNP có AB = MN, BC = NP, hai tam giác bằng nhau theo trường hợp
cạnh – góc – cạnh nếu:
A. 𝐵̂ = 𝐶̂ B. 𝐵̂ = 𝑀̂ C. 𝐵̂ = 𝑃̂ D. 𝐵̂ = 𝑁̂
Câu 7. Cho ∆ABC = ∆MNP biết góc A = 50°, góc B = 70°. Khi đó độ lớn góc P là:
A. 60° B. 70° C. 50° D. Một kết quả khác
Câu 8. Cho ∆ABC cân tại A có góc A = 40°, khi đó số đo góc B là:
A. 140° B. 40° C. 70° D. 180°
Câu 9. Cho tam giác ABC đều cạnh 6cm, vẽ AH vuông góc BC tại H. Khi đó độ dài AH là:
A. 6cm B. 3cm C. 27cm D. 3√3 cm
Câu 10. Cho tam giác MNP có MK vuông góc với NP tại K. Biết MN = 15cm, MP = 20cm, KP
= 16cm. Khi đó chu vi tam giác MNP là:
A. 58cm B. 59cm C. 60cm D. 61cm
Câu 6: B
Câu 7: A
Câu 8: C
Câu 9: D
Câu 10: C
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, có góc C = 30 độ, kẻ AH vuông góc BC (H thuộc BC). Trên đoạn HC lấy điểm D sao cho HD = HB.
a) Chứng minh tam giác AHB = tam giác AHD.
b) Chứng minh tam giác ABD là tam giác đều.
c) Từ C kẻ CE vuông góc với AD (E thuộc AD). Chứng minh DE = HB.
d) Từ D kẻ DF vuông góc với AC ( F thuộc AC), I là giao điểm của CE và AH. Chứng minh I, D, F thẳng hàng.
a: Xét ΔAHB vuông tại H và ΔAHD vuông tại H có
AH chung
HB=HD
=>ΔAHB=ΔAHD
=>AB=AD
b: Xét ΔABD có
AB=AD
góc B=60 độ
=>ΔABD đều
c: Xét ΔDAC có góc DAC=góc DCA=30 độ
nên ΔDAC cân tại D
Xét ΔDHA vuông tại H và ΔDEC vuông tại E có
DA=DC
góc ADH=góc CDE
=>ΔDHA=ΔDEC
=>AH=EC
d: Xét ΔCIA có
CH,AE là đường cao
CH cắt AE tại D
=>D là trực tâm
=>ID vuông góc AC
mà DF vuông góc AC
nên I,D,F thẳng hàng
Đúng 0
Bình luận (0)
Cho hình chữ nhật 𝐴𝐵𝐶𝐷 có 𝐴𝐵 8 𝑐𝑚, 𝐴𝐷 6 𝑐𝑚, đường chéo 𝐵𝐷. Kẻ 𝐴𝐻 ⊥ 𝐵𝐷 (𝐻 ∈ 𝐵𝐷). a Chứng minh ∆𝐴𝐻𝐷 ∽ ∆𝐵𝐴𝐷. b Tính độ dài 𝐵𝐷 và 𝐴𝐻. c Chứng minh 𝐵𝐶2DH.BD
Đọc tiếp
Cho hình chữ nhật 𝐴𝐵𝐶𝐷 có 𝐴𝐵 = 8 𝑐𝑚, 𝐴𝐷 = 6 𝑐𝑚, đường chéo 𝐵𝐷. Kẻ 𝐴𝐻 ⊥ 𝐵𝐷 (𝐻 ∈ 𝐵𝐷). a Chứng minh ∆𝐴𝐻𝐷 ∽ ∆𝐵𝐴𝐷. b Tính độ dài 𝐵𝐷 và 𝐴𝐻. c Chứng minh 𝐵𝐶2=DH.BD
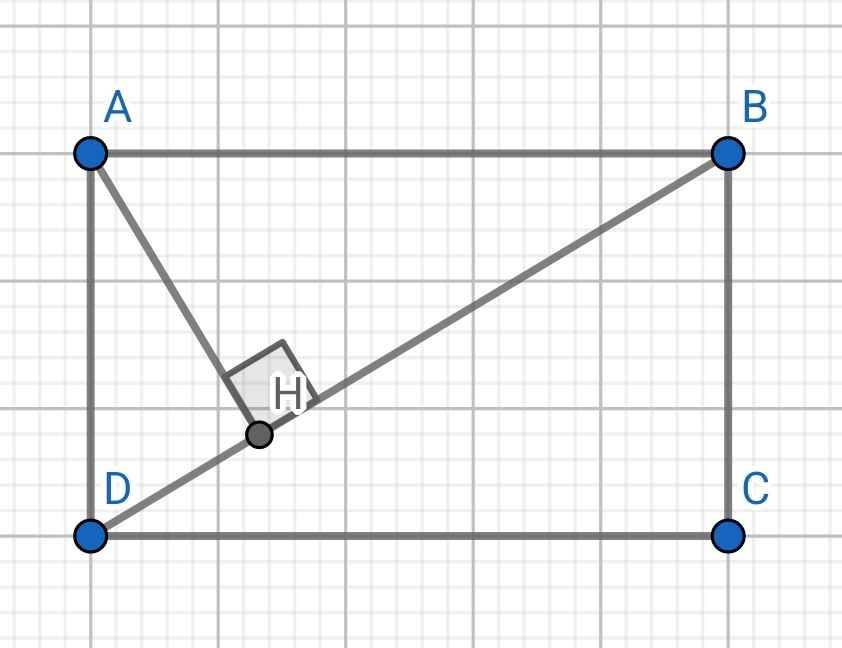
a) Xét hai tam giác vuông: ∆AHD và ∆BAD có:
∠D chung
⇒ ∆AHD ∽ ∆BAD (g-g)
b) *) Tính BD:
∆ABD vuông tại A (do ABCD là hình chữ nhật)
⇒ BD² = AB² + AD² (Pytago)
= 8² + 6²
= 100
⇒ BD = 10 (cm)
*) Tính AH:
Ta có: 1/2 . AH . BD = 1/2 . AB . AD (cùng bằng diện tích ∆ABD)
⇒ AH . BD = AB . AD
⇒ AH = (AB . AD) / BD
= 8.6/10
= 4,8 (cm)
c) Do ∆AHD ∽ ∆BAD (cmt)
⇒ AD/BD = HD/AD
⇒ AD.AD = BD.HD
⇒ AD² = BD.HD
Mà BC = AD (hai cạnh đối của hình chữ nhật)
⇒ BC² = BD.HD
Đúng 1
Bình luận (0)
a: Xet ΔAHD vuông tại H và ΔBAD vuông tại A có
góc ADH chung
=>ΔAHD đồng dạng với ΔBAD
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
AH=8*6/10=4,8cm
c: ΔABD vuông tại A có AH vuông góc BD
nên AD^2=DH*DB=BC^2
Đúng 0
Bình luận (0)
Bài 5. Cho tam giác ABC nhọn, 𝐵̂>𝐶̂, đường cao BD và CE. Trên AC lấy điểm M sao cho AM = AB. Vẽ MN vuông góc AB, MF vuông góc CE
a) Chứng minh rằng: MN = EF
b) Chứng mịnh rằng: CM = AC - AB
c) Chứng minh rằng: AC – AB > CE – BD.
Bài 5. Cho tam giác ABC nhọn, 𝐵̂>𝐶̂, đường cao BD và CE. Trên AC lấy điểm M sao cho AM = AB. Vẽ MN vuông góc AB, MF vuông góc CE
a) Chứng minh rằng: MN = EF
b) Chứng mịnh rằng: CM = AC - AB
c) Chứng minh rằng: AC – AB > CE – BD.
cho tam giác abc vuông tại a,có góc c=30 độ,kẻ ah vuông góc bc(h thuộc bc).trên đoạn hc lấy điểm d,sao cho hd=hb
a)chứng minh tam giác ahb=tam giác ahd
b)chứng minh tam giác abd là tam giác đều
c)từ c kẻ ce vuông góc với đường thẳng ad (e thuộc ad).chứng minh de=hb
a:
a: Xet ΔAHB vuông tại H và ΔAHD vuông tại H có
AH chung
HB=HD
=>ΔAHB=ΔAHD
b: Xét ΔABD có
AB=AD
góc B=60 độ
=>ΔABD đều
c: Xét ΔDAC có góc DAC=góc DCA
nên ΔDAC cân tại D
=>DA=DC
Xét ΔDHA vuông tại H và ΔDEC vuông tại E có
DA=DC
góc HDA=góc EDC
=>ΔDHA=ΔDEC
=>DH=DE
Đúng 1
Bình luận (0)


