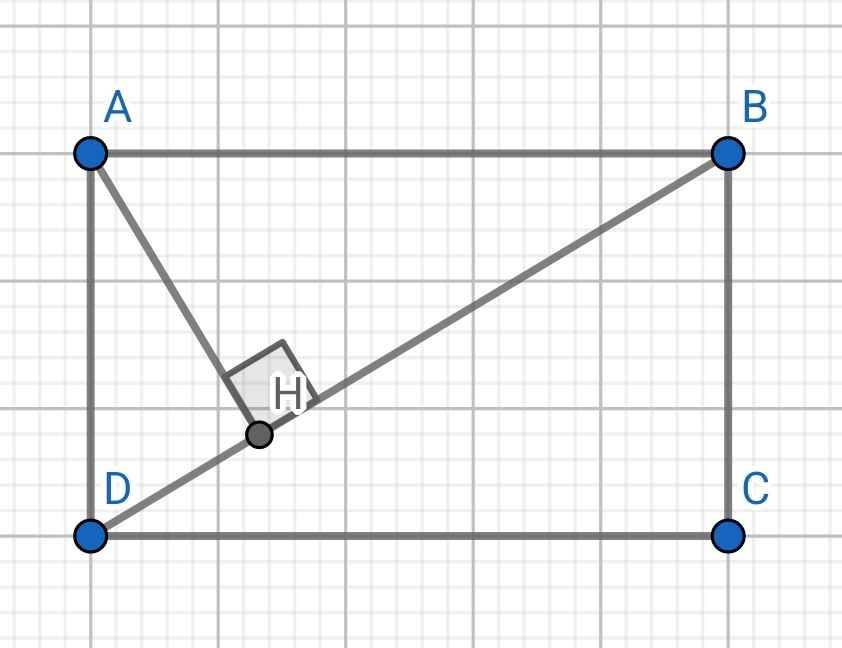
a) Xét hai tam giác vuông: ∆AHD và ∆BAD có:
∠D chung
⇒ ∆AHD ∽ ∆BAD (g-g)
b) *) Tính BD:
∆ABD vuông tại A (do ABCD là hình chữ nhật)
⇒ BD² = AB² + AD² (Pytago)
= 8² + 6²
= 100
⇒ BD = 10 (cm)
*) Tính AH:
Ta có: 1/2 . AH . BD = 1/2 . AB . AD (cùng bằng diện tích ∆ABD)
⇒ AH . BD = AB . AD
⇒ AH = (AB . AD) / BD
= 8.6/10
= 4,8 (cm)
c) Do ∆AHD ∽ ∆BAD (cmt)
⇒ AD/BD = HD/AD
⇒ AD.AD = BD.HD
⇒ AD² = BD.HD
Mà BC = AD (hai cạnh đối của hình chữ nhật)
⇒ BC² = BD.HD
a: Xet ΔAHD vuông tại H và ΔBAD vuông tại A có
góc ADH chung
=>ΔAHD đồng dạng với ΔBAD
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
AH=8*6/10=4,8cm
c: ΔABD vuông tại A có AH vuông góc BD
nên AD^2=DH*DB=BC^2


