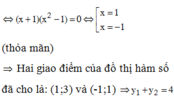tìm 2 số biết tổng của số là 2x tích của hai số là x2-y2.
NC
Những câu hỏi liên quan
bài 1: cho các hàm số y1=1/2x; y2=4; y3=-3; tìm tọa độ giao điểm của y1 với y2; y1 với y3 bằng 2 cách
bài 2 : cho hàm số y=2x biết y1;y2 là các giá trị của hàm số tương ứng với các giá trị nào của x1;x2 biết: x1*x2=5, y1.y2=7. Tính y2?
ai giúp mình với mình cần gấp bạn nào làm đúng đầu tiên mình k cho
Đúng 0
Bình luận (0)
1) Cho hệ phương trình left{{}begin{matrix}x+y3m+22x-3ym-11end{matrix}right.(m là tham số) Tìm giá trị m không âm để hệ phương trình có nghiệm (x;y) thỏa mãn (x2+1)+(y2+1)122) Tìm một số tự nhiên có hai chữ số biết rằng tổng của 5 lần chữ số hàng chục và 2 lần chuex số hàng đơn vị là 29.Nếu viết hai chữ số của nó theo thứ tự ngược lại thì số mới có hai chữ số lớn hơn số ban đầu 36 đơn vị.
Đọc tiếp
1) Cho hệ phương trình \(\left\{{}\begin{matrix}x+y=3m+2\\2x-3y=m-11\end{matrix}\right.\)
(m là tham số)
Tìm giá trị m không âm để hệ phương trình có nghiệm (x;y) thỏa mãn (x2+1)+(y2+1)=12
2) Tìm một số tự nhiên có hai chữ số biết rằng tổng của 5 lần chữ số hàng chục và 2 lần chuex số hàng đơn vị là 29.Nếu viết hai chữ số của nó theo thứ tự ngược lại thì số mới có hai chữ số lớn hơn số ban đầu 36 đơn vị.
Bài 2:
Gọi số ban đầu là \(\overline{ab}\)
Theo đề, ta có: 5a+2b=29 và 10b+a-10a-b=36
=>5a+2b=29 và -9a+9b=36
=>a=3 và b=7
Đúng 1
Bình luận (0)
Cho hàm số y= x+1/ 2x-1 , có đồ thị (H). Gọi A (x1,y1), B(x2,y2) là hai điểm phân biệt thuộc (H) sao cho tiếp tuyến của ( H) tại A,B có cùng hệ số góc k. Tìm k biết diện tích tam giác OAB bằng 1/2
\(y'=\dfrac{-3}{\left(2x-1\right)^2}\)
Tiếp tuyến tại A và B cùng hệ số góc
\(\Leftrightarrow\dfrac{-3}{\left(2x_A-1\right)^2}=\dfrac{-3}{\left(2x_B-1\right)^2}\Leftrightarrow\left(2x_A-1\right)^2-\left(2x_B-1\right)^2=0\)
\(\Leftrightarrow\left(x_A-x_B\right)\left(x_A+x_B-1\right)=0\)
\(\Leftrightarrow x_A+x_B=1\) (do A ; B phân biệt nên \(x_A-x_B\ne0\))
\(\Rightarrow x_B=1-x_A\)
Ta có: \(A\left(x_A;\dfrac{x_A+1}{2x_A-1}\right)\) ; \(B\left(1-x_A;\dfrac{x_A-2}{2x_A-1}\right)\)
\(S_{OAB}=\dfrac{1}{2}\left|\left(x_A-x_O\right)\left(y_B-y_O\right)-\left(x_B-x_O\right)\left(y_A-y_O\right)\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left|x_A\left(\dfrac{x_A-2}{2x_A-1}\right)-\left(1-x_A\right)\left(\dfrac{x_A+1}{2x_A-1}\right)\right|=1\)
\(\Leftrightarrow\left|\dfrac{2x_A^2-2x_A-1}{2x_A-1}\right|=1\) \(\Leftrightarrow\left[{}\begin{matrix}2x_A^2-2x_A-1=2x_A-1\\2x_A^2-2x_A-1=1-2x_A\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x_A^2-4x_A=0\\2x_A^2=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x_A=0\\x_A=2\\x_A=1\\x_A=-1\end{matrix}\right.\) \(\Rightarrow k=...\)
Đúng 1
Bình luận (1)
Biết rằng đồ thị hàm số
y
2
x
+
1
x
và đồ thị hàm số
y
x
2
+
x
+
1
có hai điểm chung, kí hiệu
x...
Đọc tiếp
Biết rằng đồ thị hàm số y = 2 x + 1 x và đồ thị hàm số y = x 2 + x + 1 có hai điểm chung, kí hiệu x 1 , y 1 , x 2 , y 2 là tọa độ hai điểm đó. Tìm y 1 + y 2 .
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()
Biết rằng đồ thị hàm số
y
2
x
+
1
x
và đồ thị hàm số
y
x
2
+
x
+
1
cắt nhau tại hai điểm, ký hiệu
x
1
;
y
1
,...
Đọc tiếp
Biết rằng đồ thị hàm số y = 2 x + 1 x và đồ thị hàm số y = x 2 + x + 1 cắt nhau tại hai điểm, ký hiệu x 1 ; y 1 , x 2 , y 2 là tọa độ hai điểm đó. Tìm y 1 + y 2
A. y 1 + y 2 = 0
B. y 1 + y 2 = 2
C. y 1 + y 2 = 6
D. y 1 + y 2 = 4
Cho parabol
(
P
)
:
y
2
2
x
và đường tròn
(
C
)
:
x
2
+
y
2
8
.
(P) chia (C) thành hai phần. Tìm tỉ số diện tích của hai phần đó. A.
9
π
+
2
3...
Đọc tiếp
Cho parabol ( P ) : y 2 = 2 x và đường tròn ( C ) : x 2 + y 2 = 8 . (P) chia (C) thành hai phần. Tìm tỉ số diện tích của hai phần đó.
A. 9 π + 2 3 π - 2
B. 9 π - 2 3 π - 2
C. 9 π + 2 3 π + 2
D. 9 π - 2 3 π + 2
Biết rằng đường Parabol
P
:
y
2
2
x
chia đường tròn
C
:
x
2
+
y
2
8
thành hai phần lần lượt có diện tích là
S
1
,
S
2
(hình bên). Khi đó
S...
Đọc tiếp
Biết rằng đường Parabol P : y 2 = 2 x chia đường tròn C : x 2 + y 2 = 8 thành hai phần lần lượt có diện tích là S 1 , S 2 (hình bên). Khi đó S 2 - S 1 = a π - b c với a, b, c nguyên dương và là phân số tối giản. Tổng a + b + c bằng
A. 13
B. 14
C. 15
D. 16
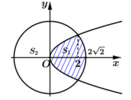
Diện tích hình tròn S = 8 π
Phương trình hoành độ giao điểm của (P) và (C) là
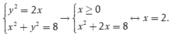
Suy ra 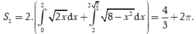
Suy ra
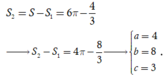
Chọn C.
Đúng 0
Bình luận (0)
Biết rằng đồ thị hàm số
y
2
x
+
1
x
và đồ thị hàm số
y
x
3
+
x
+
1
có hai điểm chung, kí hiệu
x
1
,
y
1
,...
Đọc tiếp
Biết rằng đồ thị hàm số y = 2 x + 1 x và đồ thị hàm số y = x 3 + x + 1 có hai điểm chung, kí hiệu x 1 , y 1 , x 2 , y 2 là tọa độ hai điểm đó. Tìm y 1 + y 2
A. y 1 + y 2 = 0
B. y 1 + y 2 = 4
C. y 1 + y 2 = 6
D. y 1 + y 2 = 2
cho x và y là hai đại lượng tỉ lệ nghịch . gọi x1,x2 là hai giá trị của x và y1,y2 là hai giá trị tương ứng của y, biết x1=3,4;x2=5,6 và 5y1-3y2=35,6.hãy tìm y1,y2 và hệ số tỉ lệ
x và y tỉ lệ nghịch
=>x1y1=x2y2
=>y1/x2=y2/x1
=>y1/5,6=y2/3,4=(5y1-3y2)/(5*5,6-3*3,4)=35,6/17,8=2
=>y1=11,2; y2=6,8
Đúng 0
Bình luận (0)