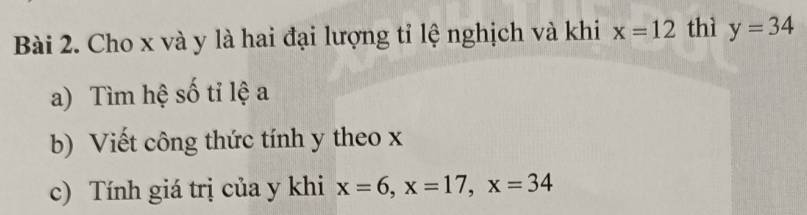tìm GTNN của A=\(\left|2\cdot x+3\right|+\left|2\cdot x-7\right|+2\cdot\left|x-1\right|+2025\)
Bài 3: Đại lượng tỉ lệ nghịch
Ba đội máy san đất làm ba khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 6 ngày và đội thứ ba trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy (có cùng năng suất) biết rằng ba đội có tất cả 13 máy.
Gọi số máy của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là a(máy),b(máy),c(máy)
(Điều kiện: \(a,b,c\in Z^+\))
Vì đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai hoàn thành công việc trong 6 ngày và đội thứ ba hoàn thành công việc trong 8 ngày nên ta có:
4a=6b=8c
=>\(\dfrac{4a}{24}=\dfrac{6b}{24}=\dfrac{8c}{24}\)
=>\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}\)
Ba đội có 13 máy nên a+b+c=13
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a+b+c}{6+4+3}=\dfrac{13}{13}=1\)
=>\(a=6\cdot1=6;b=4\cdot1=4;c=3\cdot1=3\)
Vậy: Đội thứ nhất có 6 máy
Đội thứ hai có 4 máy
Đội thứ ba có 3 máy
Đúng 1
Bình luận (0)
cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x 8 thì y 12 b) Biểu diễn y , theo x c) tính giá tị của y , khi x -4 , x 10d ) Tính giá trị của x khi y 2 , -5
Đọc tiếp
cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x = 8 thì y = 12
b) Biểu diễn y , theo x
c) tính giá tị của y , khi x = -4 , x = 10
d ) Tính giá trị của x khi y = 2 , = -5
Hệ số tỉ lệ của y đối với x:
a = x.y = 8.12 = 96
b) Biểu diễn y theo x:
y = 96/x
c) x = -4 ⇒ y = 96/(-4) = -24
x = 10 ⇒ y = 96/10 = 48/5
d) y = 2 ⇒ 96/x = 2 ⇒ x = 96/2 = 48
y = -5 ⇒ 96/x = -5 ⇒ x = 96/(-5) = -96/5
Đúng 1
Bình luận (0)
a/Hệ số tỉ lệ k của x đối với y là: \(k=xy=8.12=96\)
b/Do x và y là hai đại lượng tỉ lệ nghịch nên: \(y=\dfrac{k}{x}\)
c/- Với x = -4, ta có:
\(y=\dfrac{96}{-4}=-24\)
- Với x = 10, ta có:
\(y=\dfrac{96}{10}=9,6\)
d/\(y=\dfrac{k}{x}\)
\(\Rightarrow x=\dfrac{k}{y}\)
- Với y = 2, ta có:
\(x=\dfrac{96}{2}=48\)
- Với y = -5, ta có:
\(x=\dfrac{96}{-5}=-19,2\)
#YM
Đúng 0
Bình luận (0)
cho biết hai đại lượng y và x tỉ lệ nghịch với nhau khi x = 5 thì y = 8 khi đó y được biểu diễn theo x bởi công thức nào
Hệ số tỉ lệ của x và y là:
\(k=x\cdot y=40\)
=>\(y=\dfrac{k}{x}=\dfrac{40}{x}\)
Đúng 0
Bình luận (1)
cho biết 50 người hoàn thành một công việc trong 18 ngày . Hỏi 30 công nhân để hoàn thành công việc đó trong mấy ngày?(Năng suất các công nhân như nhau)
Để giải bài toán này, chúng ta có thể sử dụng công thức năng suất làm việc.
Năng suất làm việc của một công nhân được tính bằng công việc hoàn thành trong một đơn vị thời gian. Trong trường hợp này, năng suất của 50 công nhân là 1 công việc trong 18 ngày.
Vậy năng suất của một công nhân là 1/50 công việc trong 18 ngày.
Để tính thời gian cần thiết để 30 công nhân hoàn thành công việc, chúng ta có thể sử dụng công thức năng suất làm việc:
Năng suất của 30 công nhân = (năng suất của một công nhân) x (số công nhân)
Thời gian cần thiết = (số công việc) / (năng suất của 30 công nhân)
Vì công việc không thay đổi, số công việc là 1.
Thay vào đó, chúng ta có:
Thời gian cần thiết = 1 / [(1/50 công việc) x 30 công nhân]
Thời gian cần thiết = 1 / (1/600 công việc/ngày)
Thời gian cần thiết = 600 ngày
Vậy, 30 công nhân sẽ hoàn thành công việc trong 600 ngày.
Đúng 0
Bình luận (0)
30 công nhân sẽ hoàn thành công việc đó trong:
\(50\cdot\dfrac{18}{30}=50\cdot\dfrac{3}{5}=30\left(ngày\right)\)
Đúng 0
Bình luận (0)
x:y:z=3:5:7 và x-z =-24
Ta có: \(x:y:z=3:5:7\)
\(\Rightarrow\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau và \(x-z=-24\), ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x-z}{3-7}=\dfrac{-24}{-4}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=6\cdot3=18\\y=6\cdot5=30\\z=6\cdot7=42\end{matrix}\right.\)
Vậy: ...
Đúng 1
Bình luận (0)
a: x và y tỉ lệ nghịch theo hệ số tỉ lệ a
nên \(a=x\cdot y=12\cdot34=408\)
b: xy=408
=>\(y=\dfrac{408}{x}\)
c: Khi x=6 thì \(y=\dfrac{408}{6}=68\)
Khi x=17 thì \(y=\dfrac{408}{17}=24\)
Khi x=34 thì \(y=\dfrac{408}{34}=12\)
Đúng 1
Bình luận (0)
a: Xét ΔMAE và ΔMBC có
MA=MB
\(\widehat{AME}=\widehat{BMC}\)
ME=MC
Do đó; ΔMAE=ΔMBC
=>AE=BC
b: Xét ΔNAF và ΔNCB có
NA=NC
\(\widehat{ANF}=\widehat{CNB}\)
NF=NB
Do đó: ΔNAF=ΔNCB
=>\(\widehat{NAF}=\widehat{NCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
c: ΔMAE=ΔMBC
=>\(\widehat{MAE}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
Đúng 1
Bình luận (0)
Do năng suất của mỗi công nhân là như nhau và cùng làm một công việc nên số công nhân và số ngày hoàn thành là hai đại lượng tỉ lệ nghịch
Số công nhân hoàn thành công việc trong 8 ngày:
16 . 12 : 8 = 24 (công nhân)
Số công nhân cần tăng cường thêm:
24 - 16 = 8 (công nhân)
Đúng 2
Bình luận (0)
Để hoàn thành công việc trong 8 ngày thì số công nhân cần có là:
\(16\cdot\dfrac{12}{8}=\dfrac{16}{8}\cdot12=2\cdot12=24\left(người\right)\)
Số người cần phải tăng cường là:
24-16=8(người)
Đúng 1
Bình luận (0)
Học sinh khối 7 trồng ba loại cây phượng,bạch đàn và phi lao.Số cây phượng,bạch đàn và phi lao tỉ lệ với 8;12;15.Biết hai lần số cây phượng cộng với ba lần số cây bạch đàn nhiều hơn số cây phi lao là 74 cây.Tính số cây trồng mỗi loại.
Gọi số cây phượng, bạch đàn, phi lao lần lượt là a(cây),b(cây),c(cây)
(Điều kiện: \(a\in Z^+;b\in Z^+;c\in Z^+\))
Số cây phượng, bạch đàn, phi lao lần lượt tỉ lệ với8;12;15 nên ta có: \(\dfrac{a}{8}=\dfrac{b}{12}=\dfrac{c}{15}\)
Hai lần số cây phượng cộng với ba lần số cây bạch đàn nhiều hơn số cây phi lao là 74 cây nên ta có:
2a+3b-c=74
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{8}=\dfrac{b}{12}=\dfrac{c}{15}=\dfrac{2a+3b-c}{2\cdot8+3\cdot12-15}=\dfrac{74}{37}=2\)
=>\(a=2\cdot8=16;b=2\cdot12=24;c=2\cdot15=30\)
Vậy: Có 16 cây phượng;24 cây bạch đàn; 30 cây phi lao
Đúng 1
Bình luận (0)
Đặt số cây phượng là 8�8x, số cây bạch đàn là 12�12x và số cây phi lao là 15�15x (với �x là một số nguyên dương).
Theo thông tin "hai lần số cây phượng cộng với ba lần số cây bạch đàn nhiều hơn số cây phi lao là 74 cây", ta có phương trình:
2×(8�)+3×(12�)−15�=742×(8x)+3×(12x)−15x=74 16�+36�−15�=7416x+36x−15x=74 37�=7437x=74 �=2x=2
Vậy số cây phượng là 8�=8×2=168x=8×2=16 cây, số cây bạch đàn là 12�=12×2=2412x=12×2=24 cây và số cây phi lao là 15�=15×2=3015x=15×2=30 cây.
Đúng 0
Bình luận (0)