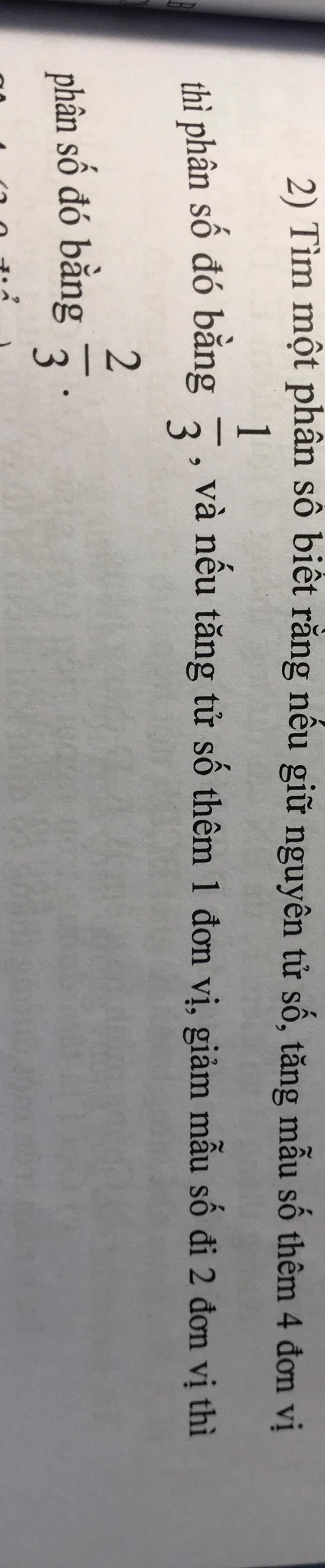
Mn giải giúp em bài này ạ
NN
Những câu hỏi liên quan
Mọi người giúp em bài này với ạ, mn giải chi tiết giúp em nha, cảm ơn mn

MN giúp em giải bài này với ạ

mn ơi, giúp em giải bài này với ạ.

Mn ơi giải giúp em mấy bài này với ạ
Câu 2:
1: \(y=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)x+4=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)\cdot x=\sqrt{3}+5-4=\sqrt{3}+1\)
=>\(x=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=\dfrac{\left(\sqrt{3}+1\right)^2}{3-1}=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}\)
2: \(x^2-2\left(1-m\right)x-2m-5=0\)
=>\(x^2+\left(2m-2\right)x-2m-5=0\)
a: \(\Delta=\left(2m-2\right)^2-4\left(-2m-5\right)\)
\(=4m^2-8m+4+8m+20\)
\(=4m^2+24>=24>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Câu 1:
2: Thay x=2 và y=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2a-\left(-1\right)=5\\b\cdot2+a\cdot\left(-1\right)=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=5+\left(-1\right)=4\\2b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\2b=a+4=6\end{matrix}\right.\)
=>a=2 và b=3
2: Gọi phân số cần tìm có dạng là \(\dfrac{a}{b}\left(b\ne0\right)\)
Khi tăng mẫu số thêm 4 đơn vị thì phân số đó bằng 1/3 nên ta có:
\(\dfrac{a}{b+4}=\dfrac{1}{3}\)
=>3a=b+4
=>3a-b=4(1)
Khi giảm mẫu số đi 2 đơn vị thì phân số bằng với 2/3 nên ta có:
\(\dfrac{a}{b-2}=\dfrac{2}{3}\)
=>3a=2(b-2)
=>3a=2b-4
=>3a-2b=-4(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a-b=4\\3a-2b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\3a-b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=8\\3a=b+4=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=8\end{matrix}\right.\)(nhận)
Vậy: Phân số cần tìm là \(\dfrac{4}{8}\)
Đúng 1
Bình luận (0)
Mn giải giúp em bài này với ạ. Em cám ơn nhiều ah
mn ơi giải giúp em bài này với ạ 🥺🙏
1654 x 1763=?
Mn giúp em giải bài này với ạ em cần gấp
Xem thêm câu trả lời
Mn cho em xin lời giải bài này ạ..... Em cảm ơn mn nhiều ạ

\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
Đúng 1
Bình luận (0)