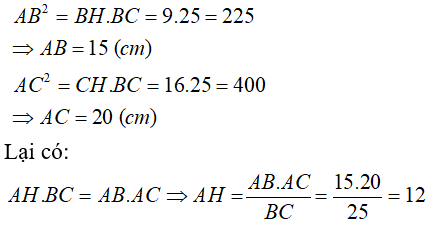Bài 1 Cho tam giác ABC vuông tại A có đường cao AH .biết BH = 9 cm ,HC = 16 cm .tính AH; AC ;số đo góc ABC (số đo góc làm tròn đến độ)
bài 2 Cho tam giác ABC vuông tại A , đường cao AH. biết AB = 3 cm ,AC = 4 cm. Tính độ dài các cạnh BC, AH và số đo góc ACB (làm tròn đến độ)