Chứng minh: a^2+b^2+c^2>=ab+bc+ac
VT
Những câu hỏi liên quan
a. Cho a^2 + b^2 + c^2 + 3= 2(a + b + c). Chứng minh rằng: a=b=c=1
b. Cho (a + b + c)^2 = 3(ab + ac + bc). Chứng minh rằng: a=b=c
c. Cho a^2 + b^2 + c^2 = ab + ac +bc. Chứng minh rằng: a=b=c
a)a2+b2+c2+3=2(a+b+c)
=>a2+b2+c2+1+1+1-2a-2b-2c=0
=>(a2-2a+1)+(b2-2b+1)+(c2-2c+1)=0
=>(a-1)2+(b-1)2+(c-1)2=0
=>a-1=b-1=c-1=0 <=>a=b=c=1
-->Đpcm
b)(a+b+c)2=3(ab+ac+bc)
=>a2+b2+c2+2ab+2ac+2bc -3ab-3ac-3bc=0
=>a2+b2+c2-ab-ac-bc=0
=>2a2+2b2+2c2-2ab-2ac-2bc=0
=>(a2- 2ab+b2)+(b2-2bc+c2) + (c2-2ca+a2) = 0
=>(a-b)2+(b-c)2+(c-a)2=0
Hay (a-b)2=0 hoặc (b-c)2=0 hoặc (a-c)2=0
=>a-b hoặc b=c hoặc a=c
=>a=b=c
-->Đpcm
c)a2+b2+c2=ab+bc+ca
=>2(a2+b2+c2)=2(ab+bc+ca)
=>2a2+2b2+c2=2ab+2bc+2ca
=>2a2+2b2+c2-2ab-2bc-2ca=0
=>a2+a2+b2+b2+c2+c2-2ab-2bc-2ca=0
=>(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ca+c2)=0
=>(a-b)2+(b-c)2+(a-c)2=0
Hay (a-b)2=0 hoặc (b-c)2=0 hoặc (a-c)2=0
=>a-b hoặc b=c hoặc a=c
=>a=b=c
-->Đpcm
Đúng 0
Bình luận (0)
a) Ta có : \(a^2+b^2+c^2+3=2\left(a+b+c\right)\)
\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2=0\)
Vì \(\left(a-1\right)^2\ge0,\left(b-1\right)^2\ge0,\left(c-1\right)^2\ge0\) nên pt trên tương đương với \(\begin{cases}\left(a-1\right)^2=0\\\left(b-1\right)^2=0\\\left(c-1\right)^2=0\end{cases}\) \(\Leftrightarrow a=b=c=1\)
b) \(\left(a+b+c\right)^2=3\left(ab+bc+ac\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=3\left(ab+bc+ac\right)\)
\(\Leftrightarrow a^2+b^2+c^2=ab+bc+ac\) (1)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)=2ab+2bc+2ac\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Mà \(\left(a-b\right)^2\ge0,\left(b-c\right)^2\ge0,\left(c-a\right)^2\ge0\)
\(\Rightarrow\begin{cases}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\\\left(c-a\right)^2=0\end{cases}\) \(\Rightarrow a=b=c\)
c) Giải tương tự câu b) , bắt đầu từ (1)
Đúng 0
Bình luận (0)
1Cho x,y >1 . Chứng minh : x2/(y-1) + y2/ (x-1) lớn hơn hoặc bằng 8
2 Cho a,b,c,d >=0 . Chứng minh : (a+b)(a+b+c)(a+b+c+d) / abcd lớn hơn hoặc bằng 64
3 Cho a,b,c >= 0 . Chứng minh : (a+b+c)(ab+bc+ac) lớn hơn hoặc bằng 8(a+b)(b+c)(c+a) / 9
4 Cho a,b,c >=0 và a+b+c =1 . Chứng minh : bc/√(a+bc) + ac/√(b+ac) + ab/√(c+ab) bé hơn hoặc bằng 1/2
xí câu 1:))
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\frac{x^2}{y-1}+\frac{y^2}{x-1}\ge\frac{\left(x+y\right)^2}{x+y-2}\)(1)
Đặt a = x + y - 2 => a > 0 ( vì x,y > 1 )
Khi đó \(\left(1\right)=\frac{\left(a+2\right)^2}{a}=\frac{a^2+4a+4}{a}=\left(a+\frac{4}{a}\right)+4\ge2\sqrt{a\cdot\frac{4}{a}}+4=8\)( AM-GM )
Vậy ta có đpcm
Đẳng thức xảy ra <=> a=2 => x=y=2
Cho ba điểm A, B, C biết :\(\frac{AB}{CB}=\frac{2}{3}\)
AB + BC + AC = 16; AC - AB = 2
a) Chứng minh CA = AB
b) Chứng minh AC = BC
Cho a,b,c là các số dương thỏa mãn 3(ab+bc+ac)=1. Chứng minh rằng a/(a^2-bc+1) +b/(b^2-ac+1) + c/(c^2-ab+1) > 1/(a+b+c)
Bài 2: Cho ΔABC vuông tại A
a) Chứng minh: \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
b) Chứng minh: \(BC^2=AB^2+AC^2-2.AB.AC.cosA\)
a) Xét ΔABC vuông tại A có
\(\left\{{}\begin{matrix}\sin\widehat{A}=\dfrac{BC}{BC}=1\\\sin\widehat{B}=\dfrac{AC}{BC}\\\sin\widehat{C}=\dfrac{AB}{BC}\end{matrix}\right.\)
Ta có: \(\dfrac{BC}{\sin\widehat{A}}=\dfrac{BC}{1}=BC\)
\(\dfrac{AC}{\sin\widehat{B}}=\dfrac{AC}{\dfrac{AC}{BC}}=BC\)
\(\dfrac{AB}{\sin\widehat{C}}=\dfrac{AB}{\dfrac{AB}{BC}}=BC\)
Do đó: \(\dfrac{BC}{\sin\widehat{A}}=\dfrac{AC}{\sin\widehat{B}}=\dfrac{AB}{\sin\widehat{C}}\)
b) Ta có: \(2\cdot AB\cdot AC\cdot\cos\widehat{A}\)
\(=2\cdot AB\cdot AC\cdot0\)
=0
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=AB^2+AC^2+2\cdot AB\cdot AC\cdot\cos\widehat{A}\)
Đúng 1
Bình luận (0)
chứng minh rằng a^2 +b^2+c^2=ab+ac+bc thì a=b=c
cho a, b, c là độ dài 3 cạnh của tam giác. Chứng minh ab+ac+bc <= a2+b2+c2 < 2 (ab+ac+bc)
Ta có (a+b)2 >=0 => a2 + 2ab + b2 >= 0 => a2 + b2 >= 2ab. (1)
(b+c)2 >=0 => b2 + 2bc + c2 >= 0 => b2 + c2 >= 2bc. (2)
(c+a)2 >=0 => c2 + 2ca + a2 >= 0 => c2 + a2 >= 2ca. (3)
Cộng (1), (2), (3), theo vế ta có 2(a2 + b2 + c2)>=2(ab+bc+ca)
suy ra a2 + b2 + c2>=ab+bc+ca (*)
Áp dụng bất đẳng thức trong tam giác ta có:
a+b>c => ac+bc>c2. (4)
b+c>a => ab+ac>a2. (5)
c+a>b => bc+ab>b2. (6)
Cộng (4), (5), (6) theo vế ta có 2(ab+bc+ca)>a2+b2+c2(**)
Từ (*) và (**) suy ra đpcm.
Đúng 0
Bình luận (0)
Trong tam giác tổng độ dài hai cạnh lớn hơn cạnh thứ 3.Vậy có:
b+c>a
Nhân 2 vế với a>0 ta có: a.b+a.c > a2 (1)
Tương tự ta có : b.c+b.a > b2 (2) và a.c+b.a > c2 (3)
Cộng vế với vế của (1),(2),(3) ta được :
2(a.b+b.c+c.a) > a2+b2+c2
Không hiểu thì nhắn tin hỏi mình nha!!!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH.
a. chứng minh AB2 = BH . BC và AC2 = CH.BC
b. Chứng minh BC2 = AB2 +AC2
c. chứng minh: AH2 = BH.CH
d. chứng minh: AH.BC=AB.AC
e. chứng minh: 1/AH2 = 1/AB2 + 1/AC2
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
Do đó: ΔABH\(\sim\)ΔCBA
Suy ra: BA/BC=BH/BA
hay \(BA^2=BH\cdot BC\)
Xét ΔACH vuông tại H và ΔBCA vuông tại A có
góc C chung
Do đo: ΔACH\(\sim\)ΔBCA
Suy ra: CA/CB=CH/CA
hay \(CA^2=CH\cdot CB\)
b: \(BC^2=AB^2+AC^2\)
c: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó: ΔAHB\(\sim\)ΔCHA
Suy ra: HA/HC=HB/HA
hay \(HA^2=HB\cdot HC\)
Đúng 0
Bình luận (0)
1) Cho a, b, c>0 và a+b+c=3. Chứng minh rằng: \(\frac{a}{b^3+ab}+\frac{b}{c^3+bc}+\frac{c}{a^3+ac}\ge\frac{3}{2}\)
2) Cho a, b, c >0 thỏa mãn: ab+ac+bc+abc=4. Chứng minh rằng: \(\sqrt{ab}+\sqrt{ac}+\sqrt{bc}\le3\)
1) \(\Sigma\frac{a}{b^3+ab}=\Sigma\left(\frac{1}{b}-\frac{b}{a+b^2}\right)\ge\Sigma\frac{1}{a}-\Sigma\frac{1}{2\sqrt{a}}=\Sigma\left(\frac{1}{a}-\frac{2}{\sqrt{a}}+1\right)+\Sigma\frac{3}{2\sqrt{a}}-3\)
\(\ge\Sigma\left(\frac{1}{\sqrt{a}}-1\right)^2+\frac{27}{2\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)}-3\ge\frac{27}{2\sqrt{3\left(a+b+c\right)}}-3=\frac{3}{2}\)
2.
Vỉ \(ab+bc+ca+abc=4\)thi luon ton tai \(a=\frac{2x}{y+z};b=\frac{2y}{z+x};c=\frac{2z}{x+y}\)
\(\Rightarrow VT=2\Sigma_{cyc}\sqrt{\frac{ab}{\left(b+c\right)\left(c+a\right)}}\le2\Sigma_{cyc}\frac{\frac{b}{b+c}+\frac{a}{c+a}}{2}=3\)
Cho o dong 2 la x,y,z nhe,ghi nham
cho tam giác abc , bc=a , ac=b , ab =c chứng minh a^2= b^2+c^2-2bc.CosA
Trong trường hợp góc A vuông thì bài toán trở thành: \(a^2=b^2+c^2\) đúng theo Pitago
Trong trường hợp góc A nhọn:
Kẻ đường cao BH (H thuộc AC) \(\Rightarrow AH=AB.cosA=c.cosA\)
Áp dụng định lý Pitago cho tam giác vuông ABH:
\(BH^2=AB^2-AH^2=c^2-AH^2\)
Áp dụng định lý Pitago cho tam giác vuông BCH:
\(BC^2=BH^2+CH^2\Leftrightarrow a^2=c^2-AH^2+CH^2\)
\(\Leftrightarrow a^2=c^2-AH^2+\left(AC-AH\right)^2=c^2-AH^2+\left(AC^2-2AC.AH+AH^2\right)\)
\(\Leftrightarrow a^2=c^2-AH^2+b^2-2b.AH+AH^2\)
\(\Leftrightarrow a^2=b^2+c^2-2b.AH=b^2+c^2-2bc.cosA\) (đpcm)
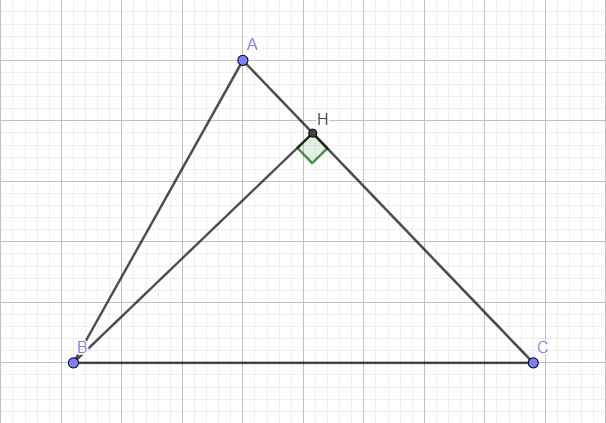
Đúng 1
Bình luận (0)
Trong trường hợp góc A tù làm hoàn toàn tương tự:
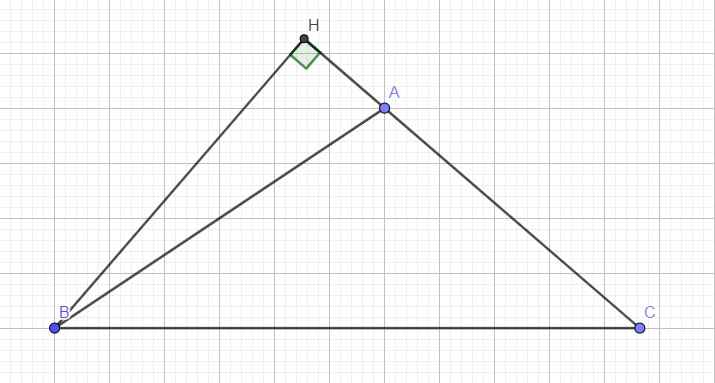
\(a^2=BH^2+CH^2=c^2-AH^2+\left(b+AH\right)^2=c^2+b^2+2b.AH\)
\(=b^2+c^2+2b.AB.cos\widehat{BAH}=b^2+c^2-2bc.cosA\)
Đúng 1
Bình luận (0)




