Trong trường hợp góc A vuông thì bài toán trở thành: \(a^2=b^2+c^2\) đúng theo Pitago
Trong trường hợp góc A nhọn:
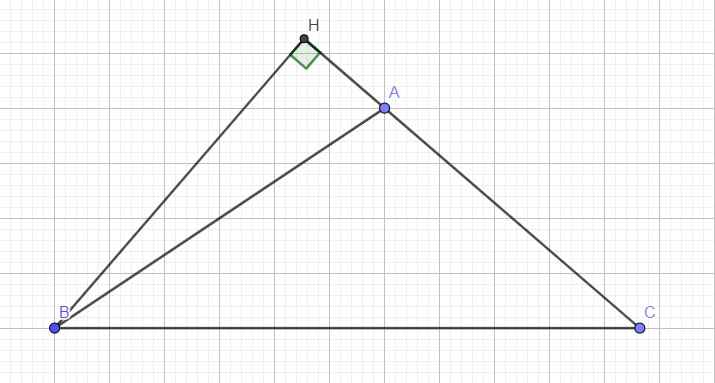
Kẻ đường cao BH (H thuộc AC) \(\Rightarrow AH=AB.cosA=c.cosA\)
Áp dụng định lý Pitago cho tam giác vuông ABH:
\(BH^2=AB^2-AH^2=c^2-AH^2\)
Áp dụng định lý Pitago cho tam giác vuông BCH:
\(BC^2=BH^2+CH^2\Leftrightarrow a^2=c^2-AH^2+CH^2\)
\(\Leftrightarrow a^2=c^2-AH^2+\left(AC-AH\right)^2=c^2-AH^2+\left(AC^2-2AC.AH+AH^2\right)\)
\(\Leftrightarrow a^2=c^2-AH^2+b^2-2b.AH+AH^2\)
\(\Leftrightarrow a^2=b^2+c^2-2b.AH=b^2+c^2-2bc.cosA\) (đpcm)
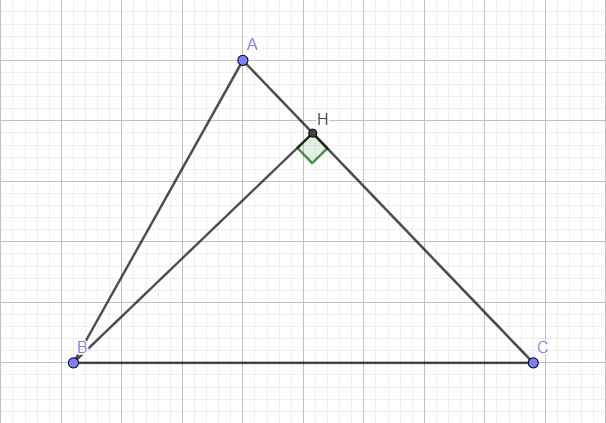
Trong trường hợp góc A tù làm hoàn toàn tương tự:
\(a^2=BH^2+CH^2=c^2-AH^2+\left(b+AH\right)^2=c^2+b^2+2b.AH\)
\(=b^2+c^2+2b.AB.cos\widehat{BAH}=b^2+c^2-2bc.cosA\)

