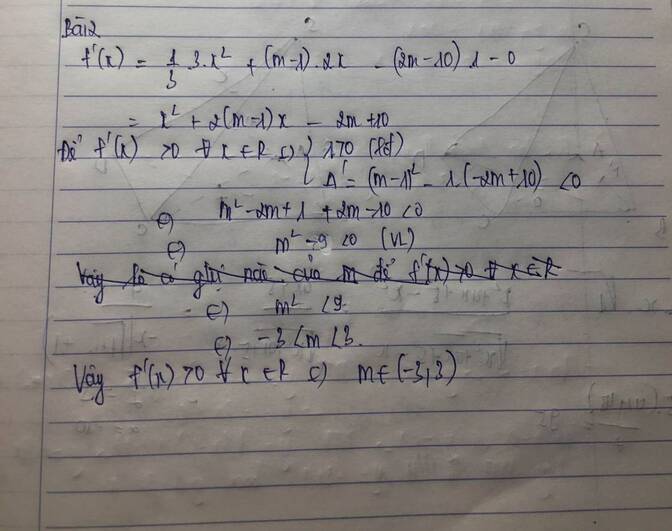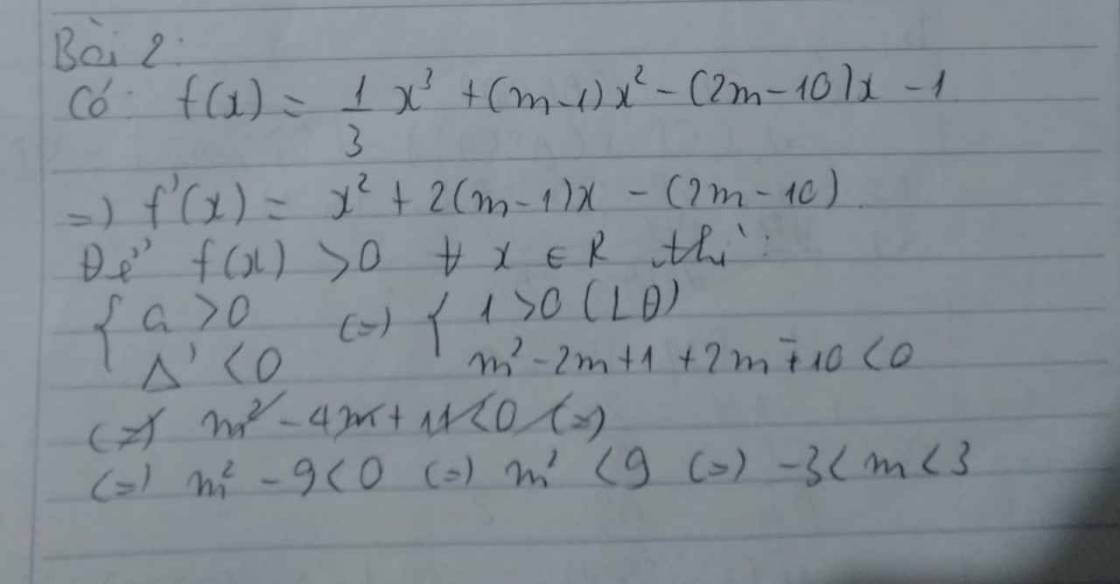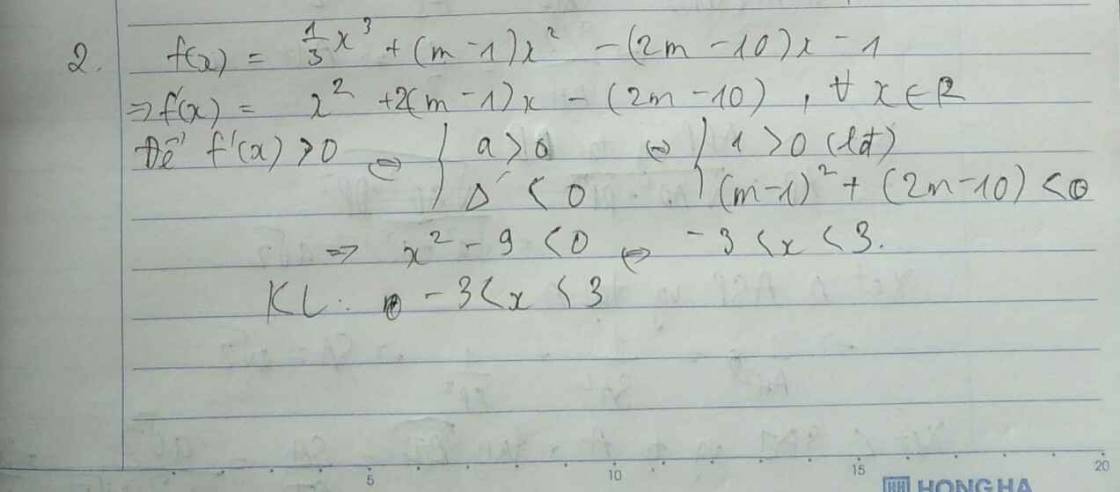Xác định tất cả các tham số m sao cho :\(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\) \(\forall x\in R\)
H24
Những câu hỏi liên quan
Xác định m để với mọi m ta có
\(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\)
Cho hàm số ( ) ( )2 2 1 2 1f x x m x m − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x Cho hàm số fleft(xright)-x^2-2left(m-1right)x+2m-1. Tìm tất cả các giá trị của tham số m để fleft(xright)0,forall xinleft(0;1right)., ( )Cho hàm số ( ) ( )2 2 1 2 1f x x m x m − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x , ( )
Đọc tiếp
Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >Cho hàm số \(f\left(x\right)=-x^2-2\left(m-1\right)x+2m-1\). Tìm tất cả các giá trị của tham số \(m\) để \(f\left(x\right)>0,\forall x\in\left(0;1\right)\).
, ( )Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >, ( )
Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)
Đúng 2
Bình luận (1)
Bài 1: Tìm m để fleft(xright)mx^2-2left(m-1right)x+4m luôn luôn âm.Bài 2: Tìm tất cả các giá trị của tham số m để bất phương trình dfrac{-x^2+2x-5}{x^2-mx+1}le0nghiệm đúng với mọi xin RBài 3: Cho hàm số fleft(xright)-x^2-2left(m-1right)x+2m-1. Tìm tất cả các giá trị của tham số m để fleft(xright)0,forall xinleft(0;1right)
Đọc tiếp
Bài 1: Tìm m để \(f\left(x\right)=mx^2-2\left(m-1\right)x+4m\) luôn luôn âm.
Bài 2: Tìm tất cả các giá trị của tham số m để bất phương trình \(\dfrac{-x^2+2x-5}{x^2-mx+1}\le0\)nghiệm đúng với mọi \(x\in R\)
Bài 3: Cho hàm số \(f\left(x\right)=-x^2-2\left(m-1\right)x+2m-1\). Tìm tất cả các giá trị của tham số m để \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
1.
Nếu \(m=0\), \(f\left(x\right)=2x\)
\(\Rightarrow m=0\) không thỏa mãn
Nếu \(x\ne0\)
Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m< 0\\\Delta'=\left(m-1\right)^2-4m^2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m< -\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
2.
\(\dfrac{-x^2+2x-5}{x^2-mx+1}\le0\forall x\)
\(\Leftrightarrow\dfrac{-\left(x-1\right)^2-4}{x^2-mx+1}\le0\forall x\)
\(\Leftrightarrow x^2-mx+1>0\forall x\)
\(\Leftrightarrow\Delta=m^2-4< 0\Leftrightarrow-2< m< 2\)
Kết luận: \(-2< m< 2\)
Đúng 0
Bình luận (0)
cho hso \(y=\dfrac{x^3}{3}-x^2+mx+m-1\). tìm tất cả các tham số m để y'≥0, \(\forall x\in\left(1,3\right)\)
\(y'=x^2-2x+m\)
\(y'\ge0\) ; \(\forall x\in\left(1;3\right)\Leftrightarrow x^2-2x+m\ge0\) ;\(\forall x\in\left(1;3\right)\)
\(\Leftrightarrow m\ge\max\limits_{\left(1;3\right)}\left(-x^2+2x\right)\)
Xét hàm \(f\left(x\right)=-x^2+2x\) trên \(\left(1;3\right)\)
\(-\dfrac{b}{2a}=1\) ; \(f\left(1\right)=1\) ; \(f\left(3\right)=-3\)
\(\Rightarrow m\ge1\)
Đúng 2
Bình luận (0)
Cho biểu thức $f\left( x \right)=\dfrac{1}{3}{{x}^{3}}+\left( m-1 \right){{x}^{2}}-\left( 2m-10 \right)x-1$ với $m$ là tham số thực. Tìm tất cả các giá trị của $m$ để ${f}'\left( x \right)>0$ $\forall x\in \mathbb{R}$.
Xem thêm câu trả lời
cho hàm số y = f(x) liên tục trên R sao cho \(\max\limits_{\left[-8;\dfrac{8}{3}\right]}=5\). xét hàm số \(g\left(x\right)=2f\left(\dfrac{1}{3}x^3-x^2-3x+1\right)+m\). tìm tất cả các giá trị thực của tham số m để \(\max\limits_{\left[-2;4\right]}g\left(x\right)=-20\)
Tìm tất cả các giá trị thực của tham số m để hàm số y = x^2 - 5x + 7 + 2m cắt trục hoành tại 2 điểm phân biệt có hoành độ thuộc [1;5]. A. \(3\le m\le7\)B. \(\dfrac{3}{4}\le m\le7\)C. \(-\dfrac{7}{2}\le m\le-\dfrac{3}{8}\)D. \(\dfrac{3}{8}\le m\le\dfrac{7}{2}\)
\(x^2-5x+7+2m=0\Leftrightarrow x^2-5x+7=-2m\)
Xét hàm \(f\left(x\right)=x^2-5x+7\) trên \(\left[1;5\right]\)
\(-\dfrac{b}{2a}=\dfrac{5}{2}\in\left[1;5\right]\)
\(f\left(1\right)=3\) ; \(f\left(\dfrac{5}{2}\right)=\dfrac{3}{4}\) ; \(f\left(5\right)=7\)
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb thuộc đoạn đã cho khi và chỉ khi:
\(\dfrac{3}{4}< -2m\le3\)
\(\Leftrightarrow-\dfrac{3}{2}\le m< \dfrac{3}{8}\)
Cả 4 đáp án đều sai là sao ta?
Đúng 3
Bình luận (8)
Tìm a sao cho ∀x, ta luôn có
-1≤\(\frac{x^2+5x+a}{2x^2-3x+2}\)≤7
\(\frac{x^2+5x+a}{2x^2-3x+2}\ge-1\Leftrightarrow\frac{x^2+5x+a}{2x^2-3x+2}+1\ge0\Leftrightarrow\frac{3x^2+2x+a+2}{2x^2-3x+2}\ge0\)
\(\Leftrightarrow3x^2+2x+a+2\ge0\) \(\forall x\) (do \(2x^2-3x+2=2\left(x-\frac{3}{4}\right)^2+\frac{7}{8}>0\))
\(\Rightarrow\Delta'=1-3\left(a+2\right)=-5-3a\le0\Rightarrow a\ge\frac{-5}{3}\) (1)
Lại có: \(\frac{x^2+5x+a}{2x^2-3x+2}\le7\Leftrightarrow\frac{x^2+5x+a}{2x^2-3x+2}-7\le0\Leftrightarrow\frac{-13x^2+26x+a-14}{2x^2-3x+2}\le0\)
\(\Leftrightarrow-13x^2+26x+a-14\le0\) \(\forall x\)
\(\Rightarrow\Delta'=169+13\left(a-14\right)\le0\Rightarrow a\le-1\) (2)
Kết hợp (1) và (2) ta được: \(\frac{-5}{3}\le a\le-1\)
Đúng 0
Bình luận (0)
Xác đinh ̣ m để với moi ̣ x ta có \(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\)
Đk: \(x\in R\)
Có \(2x^2-3x+2>0;\forall x\)
\(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\) với \(\forall x\)\(\Leftrightarrow-2x^2+3x-2\le x^2+5x+m< 14x^2-21x+14\) với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}3x^2+2x+m+2\ge0;\forall x\left(1\right)\\13x^2-26x+14-m>0;\forall x\left(2\right)\end{matrix}\right.\)
Từ \(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}a=3>0\left(lđ\right)\\\Delta\le0\end{matrix}\right.\)\(\Leftrightarrow4-4.3\left(m+2\right)\le0\)\(\Leftrightarrow-20-12m\le0\)\(\Leftrightarrow m\ge\dfrac{-5}{3}\)
Từ \(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=13>0\left(lđ\right)\\\Delta< 0\end{matrix}\right.\)\(\Leftrightarrow m< 1\)
Vậy \(-\dfrac{5}{3}\le m< 1\)
Đúng 1
Bình luận (0)