Cho dãy số (\(u_n\)) có \(u_1=2\); \(u_{n+1}=5\left(u_n-1\right)+a\). Tìm a để (\(u_n\)) là 1 cấp số nhân
JE
Những câu hỏi liên quan
Trong các dãy số cho bởi công thức truy hồi sau, dãy số nào là cấp số nhân?
A. \({u_1} = - 1,\;{u_{n + 1}} = u_n^2\) B. \({u_1} = - 1,\;{u_{n + 1}} = 2{u_n}\)
C. \({u_1} = - 1,\;{u_{n + 1}} = {u_n} + 2\) D. \({u_1} = - 1,\;{u_{n + 1}} = {u_n} - 2\)
A. Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{u_n^2}}{{{u_n}}} = {u_n}\) phụ thuộc vào n nên (\({u_n})\) thay đổi, do đó\(\left( {{u_n}} \right)\) không phải cấp số nhân.
B. Ta có: \(\frac{{{u_{n + 1}}}}{{{{u_n}}}}= 2\), do đó \(\left( {{u_n}} \right)\) là cấp số nhân với công bội \(q = 2\).
C. Ta có: \({u_{n + 1}}- {u_n} = 2\), do đó \(\left( {{u_n}} \right)\) là cấp số cộng với \(d = 2\) .
D. Ta có: \({u_{n + 1}}- {u_n} = - 2\), do đó \(\left( {{u_n}} \right)\) là cấp số cộng với \(d = -2\).
Vậy ta chọn đáp án B.
Đúng 0
Bình luận (0)
Cho dãy số \((u_n) \) thỏa mãn \(S_n=u_1+u_2+...+u_n=2^n-1\). Chứng minh rằng: dãy số \((u_n) \) là cấp số nhân.
1) cho dãy số có các số hạng đầu là 8; 15;22; 29; 36;.. số hạng tổng quát của dãy số là2) cho cấp số cộng left(u_nright) với u_12;d9. Khi đó số 2018 là số hạng thứ mấy của dãy3) cho cấp số nhân left(u_nright) có u_15;q2. Số hạng thứ 6 của cấp số nhân là4) cho cấp số nhân left(u_nright) có u_12;u_26.Công bội của cấp số nhân bằng
Đọc tiếp
1) cho dãy số có các số hạng đầu là 8; 15;22; 29; 36;.. số hạng tổng quát của dãy số là
2) cho cấp số cộng \(\left(u_n\right)\) với \(u_1=2;d=9\). Khi đó số 2018 là số hạng thứ mấy của dãy
3) cho cấp số nhân \(\left(u_n\right)\) có \(u_1=5;q=2\). Số hạng thứ 6 của cấp số nhân là
4) cho cấp số nhân \(\left(u_n\right)\) có \(u_1=2;u_2=6\).Công bội của cấp số nhân bằng
1) cho dãy số left(u_nright) xác định bởi u_nn^2-1a) tính u_1,u_2,u_3,u_4b) 99 là số hạng thứ mấy của dãy2) cho dãy số left(u_nright) xác định bởi u_ndfrac{2n-1}{n+1}a) tính u_1,u_2,u_3,u_4b) dfrac{13}{7} là số hạng thứ mấy của dãy
Đọc tiếp
1) cho dãy số \(\left(u_n\right)\) xác định bởi \(u_n=n^2-1\)
a) tính \(u_1,u_2,u_3,u_4\)
b) 99 là số hạng thứ mấy của dãy
2) cho dãy số \(\left(u_n\right)\) xác định bởi \(u_n=\dfrac{2n-1}{n+1}\)
a) tính \(u_1,u_2,u_3,u_4\)
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
2:
a: \(u_1=\dfrac{2-1}{1+1}=\dfrac{1}{2}\)
\(u_2=\dfrac{2\cdot2-1}{2+1}=1\)
\(u_3=\dfrac{2\cdot3-1}{3+1}=\dfrac{5}{4}\)
\(u_4=\dfrac{2\cdot4-1}{4+1}=\dfrac{7}{5}\)
b: Đặt \(\dfrac{2n-1}{n+1}=\dfrac{13}{7}\)
=>7(2n-1)=13(n+1)
=>14n-7=13n+13
=>n=20
=>13/7 là số hạng thứ 20 trong dãy
1:
a: u1=1^2-1=0
u2=2^2-1=3
u3=3^2-1=8
u4=4^2-1=15
b: 99=n^2-1
=>n^2=100
mà n>=0
nên n=10
=>99 là số thứ 10 trong dãy
Đúng 0
Bình luận (0)
1) cho dãy số left(u_nright) xác định bởi u_nn^2+1a) tính u_1,u_2,u_3,u_4b) 101 là số hạng thứ mấy của dãy2) cho dãy số left(u_nright) xác định bởi u_ndfrac{n+1}{2n-1}a) tính u_1,u_2,u_3,u_4b) dfrac{31}{59} là số hạng thứ mấy của dãy
Đọc tiếp
1) cho dãy số \(\left(u_n\right)\) xác định bởi \(u_n=n^2+1\)
a) tính \(u_1,u_2,u_3,u_4\)
b) 101 là số hạng thứ mấy của dãy
2) cho dãy số \(\left(u_n\right)\) xác định bởi \(u_n=\dfrac{n+1}{2n-1}\)
a) tính \(u_1,u_2,u_3,u_4\)
b) \(\dfrac{31}{59}\) là số hạng thứ mấy của dãy
1:
a:
u1=1^2+1=2
u2=2^2+1=5
u3=3^2+1=10
u4=4^2+1=17
b: Đặt 101=n^2+1
=>n^2=100
=>n=10
=>101 là số hạng thứ 10
2:
a: \(u1=\dfrac{1+1}{2-1}=2\)
\(u2=\dfrac{2+1}{2\cdot2-1}=\dfrac{3}{3}=1\)
\(u_3=\dfrac{3+1}{2\cdot3-1}=\dfrac{4}{5}\)
\(u_4=\dfrac{4+1}{2\cdot4-1}=\dfrac{5}{7}\)
b: Đặt \(\dfrac{n+1}{2n-1}=\dfrac{31}{59}\)
=>59(n+1)=31(2n-1)
=>62n-31=59n+59
=>3n=90
=>n=30
=>31/59 là số hạng thứ 30 trong dãy
Đúng 1
Bình luận (0)
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n + 1}}{n}\).
a) Cho dãy số \(\left( {{v_n}} \right)\) với \({v_n} = {u_n} - 2\). Tìm giới hạn \(\lim {v_n}\).
b) Biểu diễn các điểm \({u_1},{u_2},{u_3},{u_4}\) trên trục số. Có nhận xét gì về vị trí của các điểm \({u_n}\) khi \(n\) trở nên rất lớn?
a) \({v_n} = {u_n} - 2 = \frac{{2n + 1}}{n} - 2 = \frac{{2n + 1 - 2n}}{n} = \frac{1}{n}\).
Áp dụng giới hạn cơ bản với \(k = 1\), ta có: \(\lim {v_n} = \lim \frac{1}{n} = 0\).
b) \({u_1} = \frac{{2.1 + 1}}{1} = 3,{u_2} = \frac{{2.2 + 1}}{2} = \frac{5}{2},{u_3} = \frac{{2.3 + 1}}{3} = \frac{7}{3},{u_4} = \frac{{2.4 + 1}}{4} = \frac{9}{4}\)
Biểu diễn trên trục số:
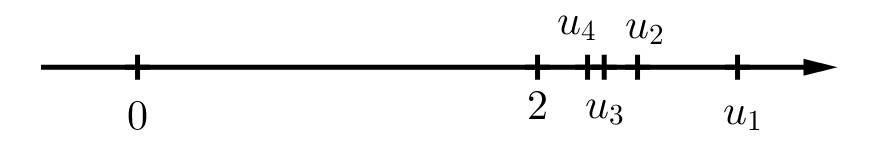
Nhận xét: Điểm \({u_n}\) càng dần đến điểm 2 khi \(n\) trở nên rất lớn.
Đúng 0
Bình luận (0)
Cho dãy số \((u_n)\) được xác định : \(\left\{ \begin{array}{l} {u_1} = 2019\\ {u_n} = - \frac{{2019}}{n}({u_1} + {u_2} + ... + {u_{n - 1}}),n > 1 \end{array} \right.\) .Tính \(T = 2{u_1} + {2^2}{u_2} + ... + {2^{2019}}{u_{2019}}\)
Cho dãy số \(\left(u_n\right)\) là một cấp số cộng có \(u_1\) = 4, công sai d = -3 và \(u_n\) = -41. Tìm n?
Cho dãy số \(\left(u_n\right)\) xác định bởi: \(u_1=\dfrac{1}{3}\) và \(u_{n+1}=\dfrac{n+1}{3n}u_n\). Tổng \(S=u_1+\dfrac{u_2}{2}+\dfrac{u_3}{3}+....+\dfrac{u_{10}}{10}\)
\(\dfrac{u_{n+1}}{n+1}=3.\dfrac{u_n}{n}\)
Đặt \(\dfrac{u_n}{n}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{3}\\v_{n+1}=3v_n\end{matrix}\right.\)
\(\Rightarrow v_n=\dfrac{1}{3}.3^{n-1}=3^{n-2}\)
\(\Rightarrow S=3^{-1}+3^0+...+3^8=...\)
Đúng 3
Bình luận (0)




