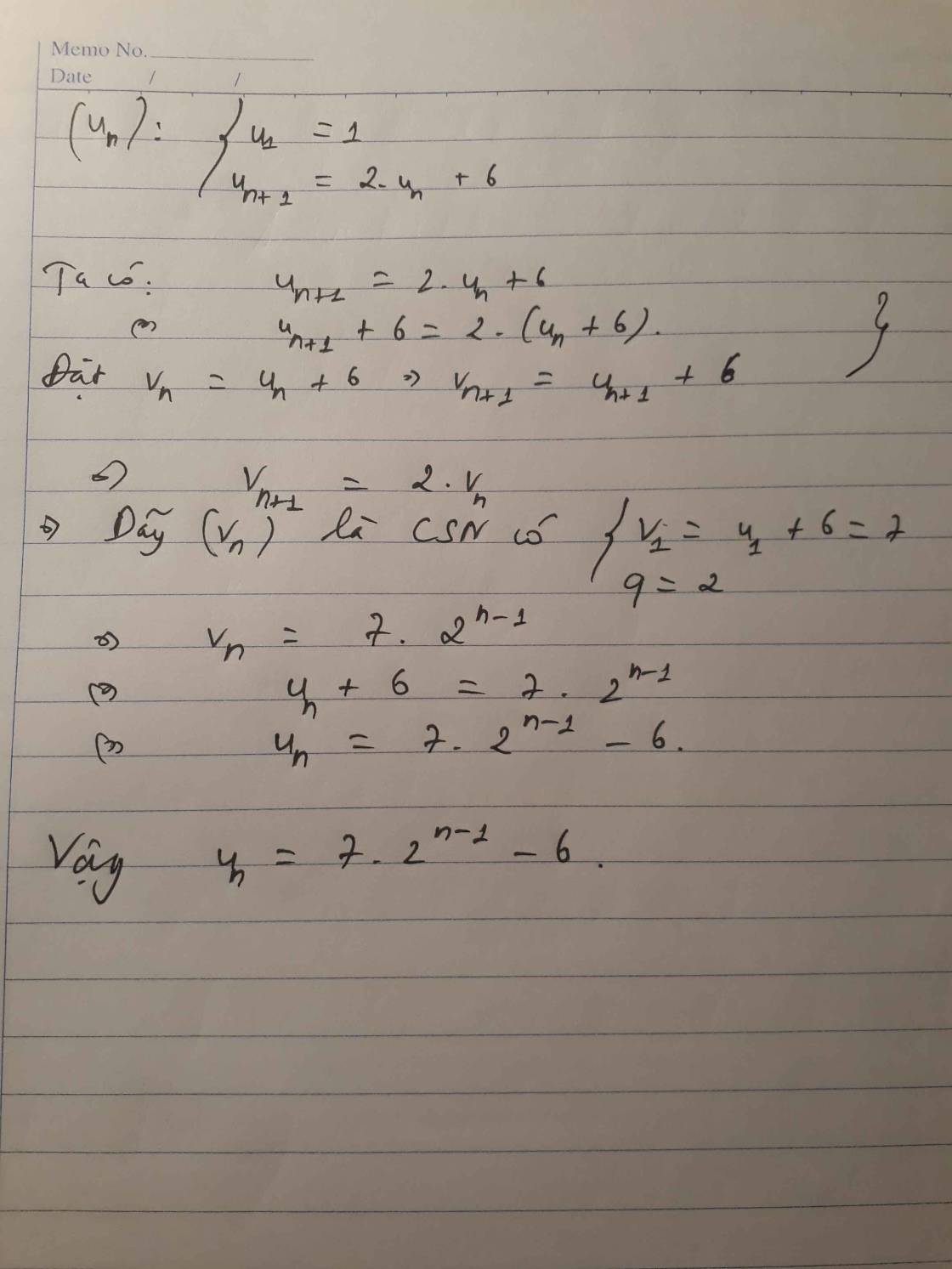Bài 4: Cấp số nhân

\(\left\{{}\begin{matrix}u1+u2+u3=13\\u4-u1=26\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}u_1+u_1\cdot q+u_1\cdot q^2=13\\u_1\cdot q^3-u_1=26\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{1+q+q^2}{\left(q-1\right)\left(q^2+q+1\right)}=\dfrac{13}{26}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{1}{q-1}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}q-1=2\\u_1=\dfrac{26}{q^3-1}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}q=2+1=3\\u_1=\dfrac{26}{3^3-1}=1\end{matrix}\right.\)

Tổng 8 số hạng đầu của cấp số nhân là:

\(\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1\cdot\left(1-3^8\right)}{1-3}=3280\)

\(\left\{{}\begin{matrix}u_1+u_2+u_3=13\\u_4-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1+u_1.q+u_1.q^2=13\\u_1.q^3-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q-1\right)\left(q^2+q+1\right)=26\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}13.\left(q-1\right)=26\\u_1.\left(q^3-1\right)=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}q=3\\u_1=1\end{matrix}\right.\)

\(S_8=\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1.\left(1-3^8\right)}{1-3}=3280\)

Để tìm U1 và q, ta sử dụng hệ phương trình sau:

Đầu tiên, ta sử dụng phương trình thứ hai để tìm U3: U3 = 60 - U4

Sau đó, thay giá trị của U3 vào phương trình thứ nhất: U1 + U6 = 165 U1 + (U3 + 3q) = 165 U1 + (60 - U4 + 3q) = 165 U1 - U4 + 3q = 105 (1)

Tiếp theo, ta sử dụng phương trình thứ nhất để tìm U6: U6 = 165 - U1

Thay giá trị của U6 vào phương trình thứ hai: U3 + U4 = 60 (60 - U4) + U4 = 60 60 = 60 (2)

Từ phương trình (2), ta thấy rằng phương trình không chứa U4, do đó không thể giải ra giá trị của U4. Vì vậy, không thể tìm được giá trị cụ thể của U1 và q chỉ từ hai phương trình đã cho.

Để tìm số hạng đầu và công bội của cấp số nhân, ta sử dụng các phương trình đã cho:

a. U4 - U2 = 72 U5 - U3 = 144

Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U4: U4 = U2 + 72

Sau đó, thay giá trị của U4 vào phương trình thứ hai: U5 - U3 = 144 (U2 + 2q) - U3 = 144 U2 - U3 + 2q = 144 (3)

Từ phương trình (3), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.

b. U1 - U3 + U5 = 65 U1 + U7 = 325

Đầu tiên, ta sử dụng phương trình thứ hai để tìm U7: U7 = 325 - U1

Sau đó, thay giá trị của U7 vào phương trình thứ nhất: U1 - U3 + U5 = 65 U1 - U3 + (U1 + 6q) = 65 2U1 - U3 + 6q = 65 (4)

Từ phương trình (4), ta thấy rằng phương trình không chứa U3, do đó không thể giải ra giá trị của U1 và q chỉ từ hai phương trình đã cho.

c. U3 + U5 = 90 U2 - U6 = 240

Đầu tiên, ta sử dụng phương trình thứ hai để tìm U6: U6 = U2 - 240

Sau đó, thay giá trị của U6 vào phương trình thứ nhất: U3 + U5 = 90 U3 + (U2 - 240 + 4q) = 90 U3 + U2 - 240 + 4q = 90 U3 + U2 + 4q = 330 (5)

Từ phương trình (5), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.

d. U1 + U2 + U3 = 14 U1 * U2 * U3 = 64

Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U3: U3 = 14 - U1 - U2

Sau đó, thay giá trị của U3 vào phương trình thứ hai: U1 * U2 * (14 - U1 - U2) = 64

Phương trình này có dạng bậc ba và không thể giải ra giá trị cụ thể của U1 và U2 chỉ từ hai phương trình đã cho.

Tóm lại, không thể tìm được giá trị cụ thể của số hạng đầu và công bội của cấp số nhân chỉ từ các phương trình đã cho.

Đáp án là C. Vì:

Gọi d là công bội của dãy cấp số nhân \((u_n) \) 

⇒ \(u_n=d.u_{n-1}=d^2.u_{n-2}=...=d^{n-2}.u_2=d^{n-1}.u_1\)

Suy ra: \(u_5=d^3.u_2 \Rightarrow d^3=\dfrac{u_5}{u_2}=\dfrac{48}{6}=8 \Rightarrow d=2\)

Có: \(u_2=d.u_1 \Leftrightarrow u_1=\dfrac{u_2}{d}=\dfrac{6}{2}=3\)

Theo đề: \(u_1+u_2+...+u_n=381 \)

\(\Leftrightarrow u_1+d.u_1+d^2.u_1+...+d^{n-1}u_1=381\)

\(\Leftrightarrow u_1(1+d+d^2+...+d^{n-1})=381\)

Mặt khác: \(u_1(1+d+d^2+...+d^{n-1})=3.\dfrac{d^n-1}{d-1} =3.\dfrac{2^n-1}{2-1}=3.(2^n-1)\)

\(\Rightarrow 3.(2^n-1)=381 \Leftrightarrow 2^n-1=127 \Leftrightarrow 2^n=128=2^7 \Rightarrow n=7\).

Vậy n = 7 thuộc (6;11)

\(\left\{{}\begin{matrix}u_5-u_1=15\\u_4-u_2=6\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}u_1.q^4-u_1=15\\u_1.q^3-u_1.q=6\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}u_1\left(q^4-1\right)=15\\u_1\left(q^3-q\right)=6\end{matrix}\right.\)

⇔ \(\dfrac{q^4-1}{q^3-q}\) = \(\dfrac{15}{6}\) ⇔ \(\dfrac{\left(q^2-1\right)\left(q^2+1\right)}{q\left(q^2-1\right)}\) = \(\dfrac{5}{2}\)

⇔ \(2q^2\)+2 - \(5q\)= 0

⇔\(\left[{}\begin{matrix}q=2\rightarrow u_1=1\\q=\dfrac{1}{2}\rightarrow u_1=-16\end{matrix}\right.\)

Lời giải:

Gọi công bội là $q$ thì 3 số hạng trên là $a; aq; aq^2$
Theo bài ra ta có:

$a+aq+aq^2=a(1+q+q^2)=\frac{a(q^3-1)}{q-1}=19(*)$

$a.aq.aq^2=(aq)^3=216=6^3$

$\Rightarrow aq=6\Rightarrow a=\frac{6}{q}$. Thay vào $(*)$ và giải pt ẩn $q$ thôi bạn. 

\(\Leftrightarrow\left\{{}\begin{matrix}u_1-u_1-2q+u_1+4q=65\\u_1+u_1+6q=325\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1+2q=65\\2u1+6q=325\end{matrix}\right.\)

=>u1=-130; q=195/2

`u_n = u_1 + (n-1).d`

`{(u_1-u_3+u_5=65),(u_1+u_7=325):}`

`<=>{(u_1-u_1-2d+u_1+4d=65),(u_1+u_1+6d=325):}`

`<=>{(u_1+2d=65),(2u_1+6d=325):}`

`<=>{(u_1=-130),(u_2=195/2):}` 

`u_n=u_1 . q^(n-1)`

`{(u_1-u_3+u_5=65),(u_1+u_7=325):}`

`<=>{(u_1 -u_1 .q^2 +u_1 .q^4=65),(u_1+u_1 .q^6=325):}`

`<=>{(u_1(1- q^2 + q^4)=65 \(1)),(u_1 .(1+q^6=325 \(2)):}`

Lấy (2) : (1) được: `(q^6+1)/(q^4-q^2+1)=5`

`<=>q=+-2`

TH1: `q=2=>u_1=5`

TH2: `q=-2=> u_1=5`

Vậy `(u_1;q)=(5;2),(5;-2)` 

Tổng số lương của chuyên gia đó sau 10 năm là:

\(S=\dfrac{10\cdot\left[2\cdot240+10\cdot1.05\right]}{2}=2452.5\left(đồng\right)\)