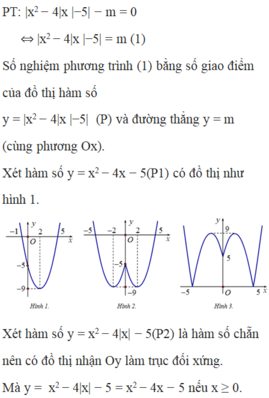
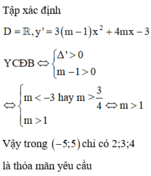Hỏi có bao nhiêu giá trị m nguyên trong nử khoảng [-10;-4] để đường thẳng d:y=(m+1)x+m+2 cắt parabol (P): \(y=x^2+x-3\) tại hai điểm phân biệt nằm về cùng 1 phía đối với trục tung
KR
Những câu hỏi liên quan
Hỏi có bao nhiêu giá trị mm nguyên trong nửa khoảng (0; 2017] để phương trình | x 2 − 4|x |−5| − m = 0 có hai nghiệm phân biệt?
A. 2016
B. 2008
C. 2009
D. 2017
Hỏi có bao nhiêu giá trị m nguyên trong đoạn
−
2017
;
2017
để hàm số
y
x
3
−
3
2
m
+
1
x
2
+
12
m
+
5
x...
Đọc tiếp
Hỏi có bao nhiêu giá trị m nguyên trong đoạn − 2017 ; 2017 để hàm số y = x 3 − 3 2 m + 1 x 2 + 12 m + 5 x − 2 đồng biến trên khoảng 2 ; + ∞ ?
A. 2018
B. 2019
C. 2017
D. 2016
Đáp án A
Để hàm số đồng biến trên khoảng 2 ; + ∞ thì
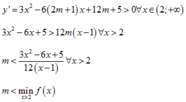
Xét f x = 3 x 2 − 6 x + 5 12 x − 1 có đạo hàm f ' x = 3 x 2 − 6 x + 1 12 x − 1 2 > 0 x > 2
Do đó f(x) đồng biến trên khoảng 2 ; + ∞ hay M i n f x = f 2 = 5 12 ⇒ m < 5 12
Lại có m ∈ − 2017 ; 2017 m ∈ ℤ .
Suy ra có 2018 giá trị của m thỏa mãn
Đúng 0
Bình luận (0)
Cho hàm số y = \(\dfrac{\left(4-m\right)\sqrt{6-x}+3}{\sqrt{6-x}+m}\) . Có bao nhiêu giá trị nguyên của m trong khoảng (-10; 10) sao cho hàm số đồng biến trên (-8; 5)
Đơn giản là hãy đặt \(\sqrt{6-x}=t\ge0\)
Do x và t nghịch biến nhau nên \(y=f\left(x\right)\) đồng biến trên \(\left(-8;5\right)\) đồng nghĩa \(y=f\left(t\right)\) nghịch biến trên \(\left(1;\sqrt{14}\right)\) (tại sao lại cho con số này nhỉ, (-10;5) chẳng hạn có tốt ko?)
\(\Leftrightarrow\left\{{}\begin{matrix}f'\left(t\right)\le0\\t+m=0\text{ vô nghiệm trên (0;\sqrt{14})}\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 1
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
x
+
2
x
+
m
đồng biến trên khoảng
-
∞
;
-
10
? A. 7. B. Vô số. C. 9. D. 8.
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + 2 x + m đồng biến trên khoảng - ∞ ; - 10 ?
A. 7.
B. Vô số.
C. 9.
D. 8.

Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án D
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên m ∈ (-10; 10) để hàm số y = m2x4 - 2(4m - 1)x2 + 1 đồng biến trên khoảng (1; +\(\infty\) )
- Với \(m=0\) thỏa mãn
- Với \(-2\left(4m-1\right)\ge0\Rightarrow m\le\dfrac{1}{4}\) hàm đồng biến trên \(\left(0;+\infty\right)\) thỏa mãn
- Xét với \(m>\dfrac{1}{4}\)
\(y'=4m^2x^3-4x\left(4m-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\sqrt{4m-1}}{m}\\x=-\dfrac{\sqrt{4m-1}}{m}\end{matrix}\right.\)
Do \(a=m^2>0\) nên hàm đồng biến trên các khoảng \(\left(-\dfrac{\sqrt{4m-1}}{m};0\right)\) và \(\left(\dfrac{\sqrt{4m-1}}{m};+\infty\right)\)
\(\Rightarrow\) Hàm đồng biến trên khoảng đã cho khi và chỉ khi:
\(\dfrac{\sqrt{4m-1}}{m}\ge1\Rightarrow4m-1\ge m^2\)
\(\Leftrightarrow m^2-4m+1\le0\Rightarrow2-\sqrt{3}\le m\le2+\sqrt{3}\)
Vậy \(\left[{}\begin{matrix}m\le\dfrac{1}{4}\\2-\sqrt{3}\le m\le2+\sqrt{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số
y
f
x
m
−
1
x
3
+
2
m
x
2
−
3
x
+
m
với m là tham số thực. Hỏi có bao nhiêu giá trị nguyên của m trong khoảng (-5;5) để hàm số f(x) đạt cực trị tại hai điểm...
Đọc tiếp
Cho hàm số y = f x = m − 1 x 3 + 2 m x 2 − 3 x + m với m là tham số thực. Hỏi có bao nhiêu giá trị nguyên của m trong khoảng (-5;5) để hàm số f(x) đạt cực trị tại hai điểm x 1 , x 2 x 1 < x 2 sao cho f x 1 > f x 2 ?
A. 3
B. 4
C. 5
D. 6
Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số
y
2
x
2
+
(
1
-
m
)
x
+
1
+
m
x
-
m
đồng biến trên khoảng...
Đọc tiếp
Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số y = 2 x 2 + ( 1 - m ) x + 1 + m x - m đồng biến trên khoảng ( 1 ; + ∞ ) ?
A. 3.
B. 1.
C. 2.
D. 0.
Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số
y
2
x
2
+
(
1
-
m
)
x
+
1
+
m
x
-
m
đồng biến trên khoản...
Đọc tiếp
Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số y = 2 x 2 + ( 1 - m ) x + 1 + m x - m đồng biến trên khoảng 1 ; + ∞ ?
A. 3.
B. 1.
C. 2.
D. 0.
Tập xác định D=R\{m}.
Ta có 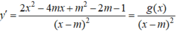
Hàm số đồng biến trên 1 ; + ∞ khi và chỉ khi g x ≥ 0 v à m ≤ 1 (1)
Vì ∆ ' g = 2 ( m + 1 ) 2 ≥ 0 , ∀ m nên (1) tương đương g(x)=0 có hai nghiệm thỏa x 1 ≤ x 2 ≤ 1
Điều kiện tương đương là
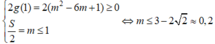
Do đó không có giá trị nguyên dương của m thỏa yêu cầu bài toán.
Chọn D.
Đúng 0
Bình luận (0)
Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số
y
x
2
-
2
m
x
+
m
+
2
x
-
m
đồng biến trên từng khoảng xác định của nó? A. Hai. B. Bốn. C. Vô số. D. Không có.
Đọc tiếp
Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số y = x 2 - 2 m x + m + 2 x - m đồng biến trên từng khoảng xác định của nó?
A. Hai.
B. Bốn.
C. Vô số.
D. Không có.