cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Xét hàm số g(x)=f(x^3+2x-1)+4m. Tìm m để ming(x)=5
Bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số
\(g’\left( x \right) = \left( {3{x^2} + 1} \right)f’\left( {{x^3} + x – 1} \right)\)
Xét \(g’\left( x \right) = 0 \Leftrightarrow f’\left( {{x^3} + x – 1} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^3} + x – 1 = – 1\\{x^3} + x – 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} + x = 0\\{x^3} + x – 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\).
\(\begin{array}{l}g\left( 0 \right) = f\left( { – 1} \right) + m = 3 + m\\g\left( 1 \right) = f\left( 1 \right) + m = – 1 + m\end{array}\)
\(\begin{array}{l} \Rightarrow \mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 0 \right)\\ \Rightarrow 3 + m = – 10\\ \Leftrightarrow m = – 13\end{array}\)
Đúng 0
Bình luận (0)
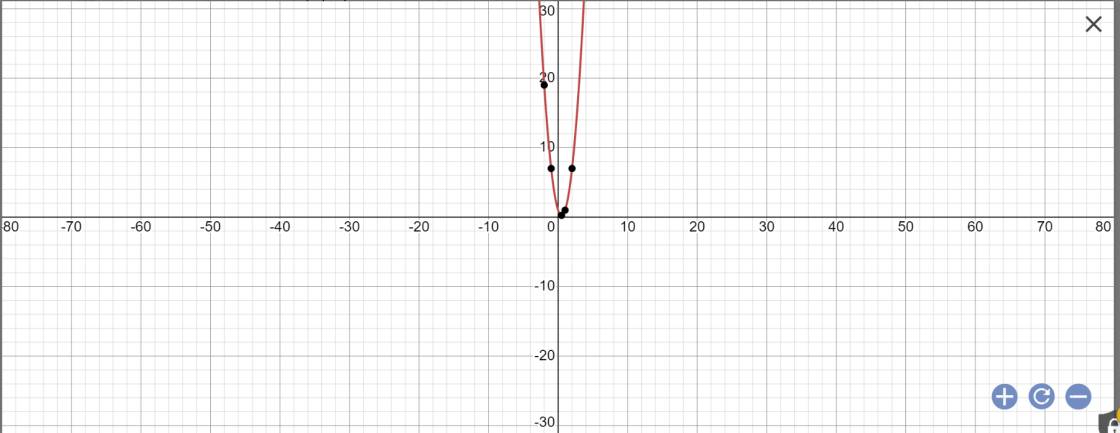
Khảo sát và vẽ đồ thị hàm số Y=-3x +3x²+1
\(y=3x^2-3x+1\)
=>\(y'=3\cdot2x-3=6x-3\)
Hàm số \(y=3x^2-3x+1\) đồng biến khi 6x-3>0
=>x>1/2
Hàm số y=3x2-3x+1 nghịch biến khi 6x-3<0
=>x<1/2
vẽ đồ thị:
Đúng 0
Bình luận (0)
Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 38: Lấy một ví dụ về hàm số dạng y = ax4 + bx2 + c sao cho phương trình y’ = 0 chỉ có một nghiệm.
Ví dụ: Hàm số y = x4 + 2x2 có y' = 4x3 + 4x
Phương trình y' = 0 chỉ có một nghiệm x = 0
Đúng 1
Bình luận (1)
Cho A là ma trận vuông cấp 4 có A = 3. Định thức của ma trận -A là:
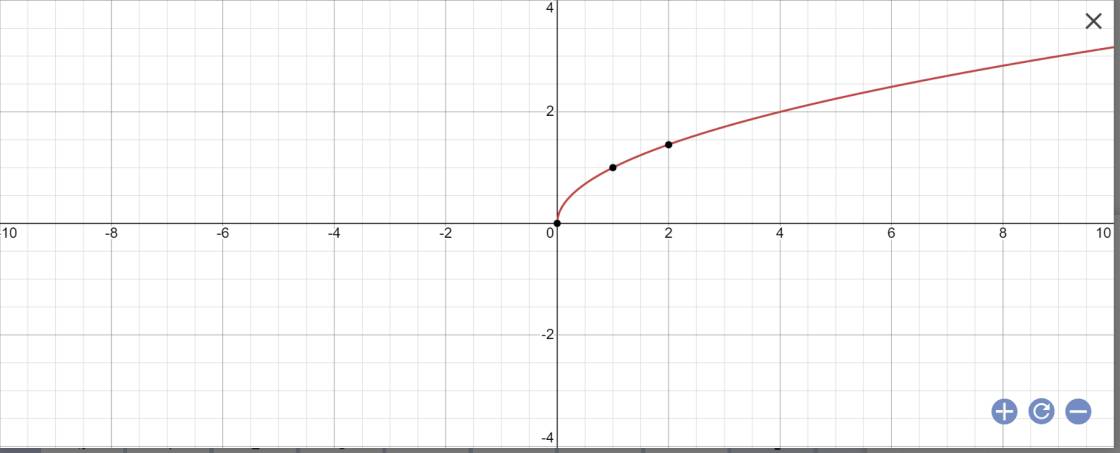
khảo sát và vẽ đồ thị hàm số \(y=\sqrt{x}\)
1,
\(f\left(x\right)=x-sin2x+2\)
\(f'\left(x\right)=1-2cos2x=0\Rightarrow cos2x=\dfrac{1}{2}\)
\(\Rightarrow2x=\dfrac{\pi}{3}+k2\pi\)
\(\Rightarrow x=\pm\dfrac{\pi}{6}+k\pi\)
\(x\in\left(-2\pi;2\pi\right)\Rightarrow x=\left\{-\dfrac{11\pi}{6};-\dfrac{7\pi}{6};-\dfrac{5\pi}{6};-\dfrac{\pi}{6};\dfrac{\pi}{6};\dfrac{5\pi}{6};\dfrac{7\pi}{6};\dfrac{11\pi}{6}\right\}\)
BBT:
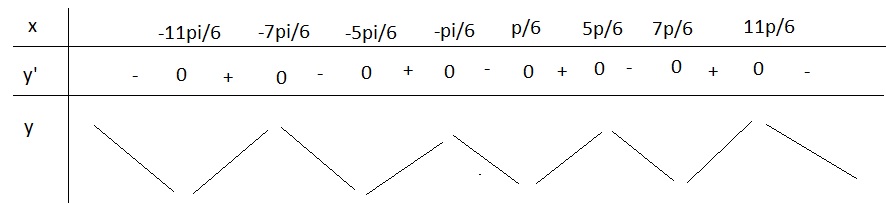
Từ BBT ta thấy trên khoảng đã cho:
Hàm đạt cực đại tại các điểm \(x=\left\{-\dfrac{7\pi}{6};-\dfrac{\pi}{6};\dfrac{5\pi}{6};\dfrac{11\pi}{6}\right\}\)
Hàm đạt cực tiểu tại các điểm \(x=\left\{-\dfrac{11\pi}{6};-\dfrac{5\pi}{6};\dfrac{\pi}{6};\dfrac{7\pi}{6}\right\}\)
Đúng 0
Bình luận (0)
2.
\(\lim\limits_{x\rightarrow\pm\infty}\dfrac{x^2+2x-3}{x^2-4x+3}=\lim\limits_{x\rightarrow\pm\infty}\dfrac{1+\dfrac{2}{x}-\dfrac{3}{x^2}}{1-\dfrac{4}{x}+\dfrac{3}{x^2}}=1\)
\(\Rightarrow y=1\) là 1 TCN của đồ thị hàm số
\(\lim\limits_{x\rightarrow1}\dfrac{x^2+2x-3}{x^2-4x+3}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x-1\right)\left(x-3\right)}=\lim\limits_{x\rightarrow1}\dfrac{x+3}{x-3}=-2\)
\(\Rightarrow x=1\) không là tiệm cận
\(\lim\limits_{x\rightarrow3^+}\dfrac{x^2+2x-3}{x^2-4x+3}=\lim\limits_{x\rightarrow3^+}\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x-1\right)\left(x-3\right)}=\lim\limits_{x\rightarrow3^+}\dfrac{x+3}{x-3}=+\infty\)
\(\Rightarrow x=3\) là TCĐ của ĐTHS
Vậy ĐTHS đã cho có 1 TCĐ là \(x=3\) và 1 TCN \(y=1\)
Đúng 0
Bình luận (0)
3.
Pt hoành độ giao điểm:
\(\left(x+1\right)\left(x^2+2mx+m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\f\left(x\right)=x^2+2mx+m+2=0\left(1\right)\end{matrix}\right.\)
ĐTHS cắt trục hoành tại 3 điểm pb khi và chỉ khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(-1\right)=1-2m+m+2\ne0\\\Delta'=m^2-m-2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\2< m< 3\\m>3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Ai giúp mình với 
Y=x3+2x2+5x+1
Cho hàm số ydfrac{ax+b}{cx+d} có đồ thị hình vẽ bên dưới, trong đó d0. Trong các số a,b,c có bao nhiêu số dương? A.0 B.1 C.2 D.3
Đọc tiếp
Cho hàm số \(y=\dfrac{ax+b}{cx+d}\) có đồ thị hình vẽ bên dưới, trong đó d<0. Trong các số a,b,c có bao nhiêu số dương?
A.0 B.1 C.2 D.3
Ta có : \(y=\dfrac{ax+b}{cx+d}\left(x\ne\dfrac{-d}{c}\right)\)
Nhìn vào đồ thị ; ta thấy : ĐTHS có TCĐ là : \(x=-\dfrac{d}{c}>0\)
TCN : \(y=\dfrac{a}{c}>0\)
Vì d < 0 suy ra : c > 0 ; a > 0
ĐTHS cắt Ox tại điểm x = \(-\dfrac{b}{a}< 0\) \(\Rightarrow b>0\)
Chọn D
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và vẽ đồ thị hàm số y=1/4X4+X2-2
\(y=\dfrac{1}{4}x^4+x^2-2\)
Tập xác định: \(D=R\)
Ta có:
\(y'=x^3+2x=x\left(x^2+2\right)\)
\(y'=0\Leftrightarrow x=0\)
\(\lim\limits_{x\rightarrow\pm\infty}\)\(y=\infty\)
Ta có bảng biến thiên
| \(x\) | \(-\infty\) \(0\) \(+\infty\) |
| \(y'\) | \(-\) \(0\) \(+\) |
| \(y\) |
Đúng 0
Bình luận (0)