Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc B A D ^ = 60 ° , AB’ hợp với đáy (ABCD) một góc 30 ° . Thể tích khối hộp là:
A. a 3 2
B. a 3 6
C. 3 a 3 2
D. a 3 3 6
PB
Những câu hỏi liên quan
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc BAD
60
o
AB’ hợp với đáy (ABCD) một góc
30
o
Thể tích khối hộp là:
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và góc BAD= 60 o AB’ hợp với đáy (ABCD) một góc 30 o Thể tích khối hộp là:
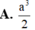
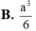
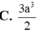
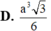
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a và AC = a. SO vuông góc với đáy và SO = \(\dfrac{a\sqrt{3}}{2}\) .
a. Chứng minh (SAC) vuông góc với (SBD)
b. Tính góc giữa SB và (SCD)
c. Gọi M là trung điểm của AB. Tính khoảng cách giữa SM và CD
Cho hình chóp SABCD có SA=SB=SD =( a căn 3)/2 , đáy là hình thoi cạnh a và góc A = 60°
a) Cm ( SAC) vuông góc ( ABCD) và SB vuông góc với BC
b) Tính góc giữa hai mặt phẳng ( SBD) và ( ABCD )
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật
A
B
a
,
A
D
2
a
, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng
2
a
3
3
. Tính góc tạo bởi đường thẳng SB với măṭ phẳng ( ABCD). A
75
°
B.
45
°...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật A B = a , A D = 2 a , cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng 2 a 3 3 . Tính góc tạo bởi đường thẳng SB với măṭ phẳng ( ABCD).
A 75 °
B. 45 °
C. 60 °
D. 30 °
Đáp án B
Ta có S A B C D = 2 a 2 ⇒ S A = 3 V S A B C D = a
Lại có S B ; A B C D ^ = S B A ^ , mặt khác tan S B A ^ = 1 ⇒ S B A ^ = 45 °
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật ABa, AD2a, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng
2
a
3
3
. Tính góc tạo bởi đường thẳng SB với măṭ phẳng ( ABCD).
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật AB=a, AD=2a, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng 2 a 3 3 . Tính góc tạo bởi đường thẳng SB với măṭ phẳng ( ABCD).
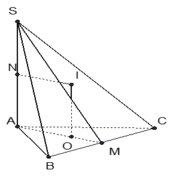
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, cạnh 2a, góc ABC bằng 60 độ, SA bằng SC, SB bằng SD góc giữa SA và mặt phẳng ABCD bằng 45 độ. Chứng minh: SO vuông với mặt phẳng ABCD, tính a theo thể tích khối S.ABCD
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC. A.
3
πa
2
7
B.
7
πa
2
12
C.
7...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
A. 3 πa 2 7
B. 7 πa 2 12
C. 7 πa 2 3
D. πa 2 7
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, cạnh 2a, góc ABC bằng 60 độ, SA bằng SC, SB bằng SD góc giữa SA và mặt phẳng ABCD bằng 45 độ. Chứng minh: SO vuông với mặt phẳng ABCD, tính a theo thể tích khối S.ABCD
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a. Tính thể tích V của mặt cầu ngoại tiếp hình chóp S.ABC.
Gọi M là trung điểm SA và O là tâm đáy \(\Rightarrow AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AM=\dfrac{a}{2}\)
Qua O kẻ đường thẳng d song song SA, trong mặt phẳng (SAO) qua M kẻ đường thẳng song song AO cắt d tại I
\(\Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp
\(R=IA=\sqrt{IM^2+AM^2}=\sqrt{AO^2+AM^2}=\dfrac{a\sqrt{21}}{6}\)
Đúng 1
Bình luận (0)