Đạo hàm của hàm số y = xsinx bằng:
A. y ' = sin x - x cos x
B. y ' = sin x + x cos x
C. y ' = - x cos x
D. y ' = x cos x
Bằng cách viết \(y = \cos x = \sin \left( {\frac{\pi }{2} - x} \right),\) tính đạo hàm của hàm số \(y = \cos x.\)
\(y'=\left(cosx\right)'\\ =\left(\dfrac{\pi}{2}-x\right)'cos\left(\dfrac{\pi}{2}-x\right)\\ =-cos\left(\dfrac{\pi}{2}-x\right)\\ =-sinx\)
Tính đạo hàm của các hàm số sau:
a) \(y = x{\sin ^2}x;\)
b) \(y = {\cos ^2}x + \sin 2x;\)
c) \(y = \sin 3x - 3\sin x;\)
d) \(y = \tan x + \cot x.\)
tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
Tìm đạo hàm y' của hàm số y = sin x + cos x
A. y' = 2cosx
B. y' = 2sinx
C. y' = sinx - cosx
D. y' = cosx - sinx
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
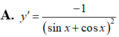
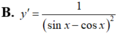
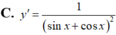

Tính đạo hàm của hàm số sau y = sin x sin x - cos x
![]()
![]()
![]()
![]()
Tính đạo hàm của các hàm số sau:
a) \(y = \sin 3x\);
b) \(y = {\cos ^3}2x\);
c) \(y = {\tan ^2}x\);
d) \(y = \cot \left( {4 - {x^2}} \right)\).
a) Đặt \(u = 3{\rm{x}}\) thì \(y = \sin u\). Ta có: \(u{'_x} = {\left( {3{\rm{x}}} \right)^\prime } = 3\) và \(y{'_u} = {\left( {\sin u} \right)^\prime } = \cos u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = \cos u.3 = 3\cos 3{\rm{x}}\).
Vậy \(y' = 3\cos 3{\rm{x}}\).
b) Đặt \(u = \cos 2{\rm{x}}\) thì \(y = {u^3}\). Ta có: \(u{'_x} = {\left( {\cos 2{\rm{x}}} \right)^\prime } = - 2\sin 2{\rm{x}}\) và \(y{'_u} = {\left( {{u^3}} \right)^\prime } = 3{u^2}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 3{u^2}.\left( { - 2\sin 2{\rm{x}}} \right) = 3{\left( {\cos 2{\rm{x}}} \right)^2}.\left( { - 2\sin 2{\rm{x}}} \right) = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
Vậy \(y' = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
c) Đặt \(u = \tan {\rm{x}}\) thì \(y = {u^2}\). Ta có: \(u{'_x} = {\left( {\tan {\rm{x}}} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\) và \(y{'_u} = {\left( {{u^2}} \right)^\prime } = 2u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 2u.\frac{1}{{{{\cos }^2}x}} = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
Vậy \(y' = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
d) Đặt \(u = 4 - {x^2}\) thì \(y = \cot u\). Ta có: \(u{'_x} = {\left( {4 - {x^2}} \right)^\prime } = - 2{\rm{x}}\) và \(y{'_u} = {\left( {\cot u} \right)^\prime } = - \frac{1}{{{{\sin }^2}u}}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = - \frac{1}{{{{\sin }^2}u}}.\left( { - 2{\rm{x}}} \right) = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
Vậy \(y' = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
a) Bằng cách viết \(y = \tan x = \frac{{\sin x}}{{\cos x}}\,\,\,\left( {x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right),\) tính đạo hàm của hàm số \(y = \tan x.\)
b) Sử dụng đẳng thức \(\cot x = \tan \left( {\frac{\pi }{2} - x} \right)\) với \(x \ne k\pi \left( {k \in \mathbb{Z}} \right),\) tính đạo hàm của hàm số \(y = \cot x.\)
\(a,y'=\left(tanx\right)'=\left(\dfrac{sinx}{cosx}\right)'\\ =\dfrac{\left(sinx\right)'cosx-sinx\left(cosx\right)'}{cos^2x}\\ =\dfrac{cos^2x+sin^2x}{cos^2x}\\ =\dfrac{1}{cos^2x}\\ b,\left(cotx\right)'=\left[tan\left(\dfrac{\pi}{2}-x\right)\right]'\\ =-\dfrac{1}{cos^2\left(\dfrac{\pi}{2}-x\right)}\\ =-\dfrac{1}{sin^2\left(x\right)}\)
Tìm đạo hàm của các hàm số sau :
a) \(y=5\sin x-3\cos x\)
b) \(y=\dfrac{\sin x+\cos x}{\sin x-\cos x}\)
c) \(y=x\cos x\)
d) \(y=\dfrac{\sin x}{x}+\dfrac{x}{\sin x}\)
e) \(y=\sqrt{1+2\tan x}\)
f) \(y=\sin\sqrt{1+x^2}\)
a) y' = 5cosx -3(-sinx) = 5cosx + 3sinx;
b) =
=
.
c) y' = cotx +x. = cotx -
.
d) +
=
= (x. cosx -sinx)
.
e) =
=
.
f) y' = (√(1+x2))' cos√(1+x2) = cos√(1+x2) =
cos√(1+x2).
Tính đạo hàm của mỗi hàm số sau:
a) \(y = \left( {{x^2} + 2x} \right)\left( {{x^3} - 3x} \right)\)
b) \(y = \frac{1}{{ - 2x + 5}}\)
c) \(y = \sqrt {4x + 5} \)
d) \(y = \sin x\cos x\)
e) \(y = x{e^x}\)
f) \(y = {\ln ^2}x\)
a: \(y'=\left(x^2+2x\right)'\left(x^3-3x\right)+\left(x^2+2x\right)\left(x^3-3x\right)'\)
\(=\left(2x+2\right)\left(x^3-3x\right)+\left(x^2+2x\right)\left(3x^2-3\right)\)
\(=2x^4-6x^2+2x^3-6x+3x^4-3x^2+6x^3-6x\)
\(=5x^4+8x^3-9x^2-12x\)
b: y=1/-2x+5
=>\(y'=\dfrac{2}{\left(2x+5\right)^2}\)
c: \(y'=\dfrac{\left(4x+5\right)'}{2\sqrt{4x+5}}=\dfrac{4}{2\sqrt{4x+5}}=\dfrac{2}{\sqrt{4x+5}}\)
d: \(y'=\left(sinx\right)'\cdot cosx+\left(sinx\right)\cdot\left(cosx\right)'\)
\(=cos^2x-sin^2x=cos2x\)
e: \(y=x\cdot e^x\)
=>\(y'=e^x+x\cdot e^x\)
f: \(y=ln^2x\)
=>\(y'=\dfrac{\left(-1\right)}{x^2}=-\dfrac{1}{x^2}\)
Tính đạo hàm của các hàm số sau:
a) y=\(\dfrac{3x^2-18x-2}{1-2x}-\dfrac{2x-3}{x+4}\)
b) y=\(-\dfrac{\sin x}{3\cos^3x}+\dfrac{4}{3}\tan x\)