Bài 3: Đạo hàm của hàm số lượng giác

\(y'=2021\cdot cos\left(x\sqrt{x}\right)^{2020}\cdot\left(cos\left(x\sqrt{x}\right)\right)'\)

\(=2021\cdot\left(-x\sqrt{x}\right)'\cdot sin\left(x\sqrt{x}\right)\cdot cos\left(x\sqrt{x}\right)^{2020}\)

\(=-2021\cdot\dfrac{\left(x^3\right)'}{2\sqrt{x^3}}\cdot sin\left(x\sqrt{x}\right)\cdot cos^{2020}x\sqrt{x}\)

\(=-2021\cdot\dfrac{3x^2}{2x\sqrt{x}}\cdot sin\left(x\sqrt{x}\right)\cdot cos^{2020}x\sqrt{x}\)

\(=-\dfrac{6063}{2}\sqrt{x}\cdot sin\left(x\sqrt{x}\right)\cdot cos^{2020}x\sqrt{x}\)

Đề là: `y'=0 AA x in RR` nhỉ?

-Giải-

Ta có: `y'=0`

`<=>3/2x^2-2(m+2)+m+2=0`   `(1)`

Để `(1)` có nghiệm `AA m in RR<=>\Delta' >= 0`

                  `<=>[-(m+2)]^2-3/2(m+2) >= 0`

                  `<=>m^2+4m+4-3/2m-3 >= 0`

                   `<=>[(m <= -2),(m >= -1/2):}`

Ta có : \(f'\left(x\right)=\left(sin3x\right)'.cos4x+\left(cos4x\right)'.sin3x+\left(tanx\right)'\)

\(\Rightarrow f'\left(x\right)=3cos3x.cos4x-4sin4x.sin3x+\dfrac{1}{cos^2x}\)

\(y=\dfrac{x-1}{x+2}\left(x\ne-2\right)\Rightarrow y'=\dfrac{\left(x+2\right)-\left(x-1\right)}{\left(x+2\right)^2}=\dfrac{3}{\left(x+2\right)^2}\)

Giả sử d là tiếp tuyến cần tìm của đths trên 

a. d đi qua \(N\left(-1;-2\right)\) . Suy ra : HSG của d : \(\dfrac{3}{\left(-1+2\right)^2}=3\)

PTTT d : \(y=3\left(x+1\right)-2=3x+1\)

b.d có hđtđ \(x_o=3\) \(\Rightarrow y_o=\dfrac{3-1}{3+2}=\dfrac{2}{5};y'=\dfrac{3}{25}\)

PTTT d : \(y=\dfrac{3}{25}\left(x-3\right)+\dfrac{2}{5}=\dfrac{3x}{25}+\dfrac{1}{25}\)

c. Tung độ tiếp điểm yo = 9 nên : \(\dfrac{x_o-1}{x_o+2}=9\Leftrightarrow x_o=-\dfrac{19}{8}\)

y' = 64/3

PTTT d : \(y=\dfrac{64}{3}\left(x+\dfrac{19}{8}\right)+9=\dfrac{64}{3}x+\dfrac{179}{3}\)

d. Ta có : \(\dfrac{3}{\left(x_o+2\right)^2}=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}x_o+2=3\\x_o+2=-3\end{matrix}\right.\)  \(\Leftrightarrow\left[{}\begin{matrix}x_o=1\\x_o=-5\end{matrix}\right.\)

Với xo = 1 \(\Rightarrow y_o=0\) . PTTT d : y = 1/3(x-1) = 1/3x - 1/3

Với xo = -5 \(\Rightarrow y_o=2\) . PTTT d : \(y=\dfrac{1}{3}\left(x+5\right)+2=\dfrac{1}{3}x+\dfrac{11}{3}\)

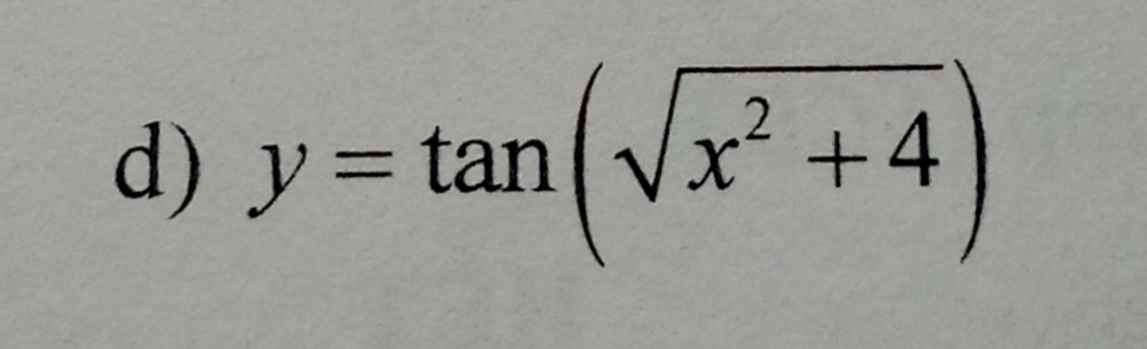
\(y=tan\left(\sqrt{x^2+4}\right)\Rightarrow y'=\dfrac{1}{cos^2\left(\sqrt{x^2+4}\right)}.\left(\sqrt{x^2+4}\right)'\)

\(\left(\sqrt{x^2+4}\right)'=\dfrac{1}{2\sqrt{x^2+4}}\left(x^2+4\right)'=\dfrac{2x}{2\sqrt{x^2+4}}=\dfrac{x}{\sqrt{x^2+4}}\)

Suy ra : \(y'=\dfrac{x}{cos^2\left(\sqrt{x^2+4}\right).\sqrt{x^2+4}}\)

Câu 13.

\(y'=\left[sin\left(\dfrac{\pi}{6}-3x\right)\right]'=\left(\dfrac{\pi}{6}-3x\right)'.cos\left(\dfrac{\pi}{6}-3x\right)=-3cos\left(\dfrac{\pi}{6}-3x\right)\)

Câu 14.

\(y'=\left[-\dfrac{1}{2}sin\left(\dfrac{\pi}{3}-x^2\right)\right]'=-\dfrac{1}{2}\left(\dfrac{\pi}{3}-x^2\right)'.cos\left(\dfrac{\pi}{3}-x^2\right)\\ =-\dfrac{1}{2}.\left(-2x\right).cos\left(\dfrac{\pi}{3}-x^2\right)=x.cos\left(\dfrac{\pi}{3}-x^2\right)\)

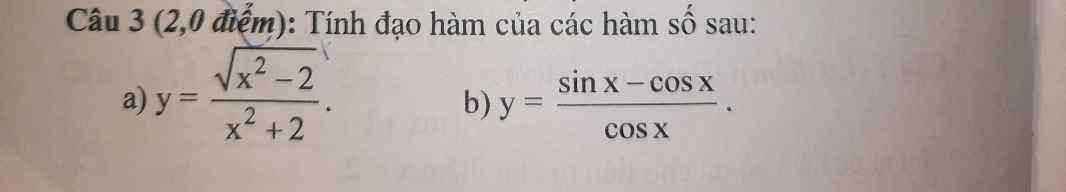
a.\(y=\dfrac{\sqrt{x^2-2}}{x^2+2}\Rightarrow y'=\dfrac{\left(\sqrt{x^2-2}\right)'\left(x^2+2\right)-\left(x^2+2\right)'.\sqrt{x^2-2}}{\left(x^2+2\right)^2}\)

\(\Rightarrow y'=\dfrac{\dfrac{x}{\sqrt{x^2-2}}\left(x^2+2\right)-2x\sqrt{x^2-2}}{\left(x^2+2\right)^2}\)  

\(=\dfrac{x\left(x^2+2\right)-2x\left(x^2-2\right)}{\left(x^2+2\right)^2\sqrt{x^2-2}}=\dfrac{-x^3+6x}{\left(x^2+2\right)^2\sqrt{x^2-2}}\)

b. \(y=\dfrac{sinx-cosx}{cosx}=tanx-1\Rightarrow y'=\dfrac{1}{cos^2x}\)